Ручная настройка PID регулятора
Окружение для ручной настройки PID регулятора
В этом проекте предлагаем вам применить минималистичное окружение для настройки PID регуляторов для графической модели системы.
Описание системы
Имеется модель, заданная в виде передаточной функции следующего вида:
Задача состоит в том, чтобы найти параметры PID регулятора, при которых система удовлетворительно отрабатывает единичное ступенчатое воздействие.
Шаги решения
Если эта модель решается в редакторе моделей, но не демонстрирует интересующих нас параметров переходного процесса, приходит время перейти к следующему этапу и попробовать огрубленно подобрать параметры вручную.
Поскольку мы заведомо не знаем масштаб нужных параметров, в этом примере подбор каждого параметра PID регулятора осуществляется двумя числами:
-
максимальное значение (без ограничений),
-
пропорциональный коэффициент (от 0 до 1)
Такой метод обеспечивает некоторый компромисс между удобством и широтой подбираемых параметров. Не внося модификаций в код программы, проектировщик может выставить любой масштаб коэффициентов регулятора, а потом плавно подбирать более точное значение при помощи плавного регулятора.
gr()
engee.open("pid_manual_tuning.engee")
using DataFrames, Statistics
all_runs = DataFrame[];
colors = [1, "skyblue", "lightblue", "powderblue", "lightblue1"];
Код следующей ячейки можно спрятать, если дважды кликнуть по форме с элементами управления. Кроме того, вывод ячейки удобно расположить справа от формы ввода параметров (кнопка ).
StopTime = 30 # @param {type:"slider",min:0,max:100,step:1}
P_max = 6.0 # @param {type:"number",placeholder:"1.0"}
I_max = 1.0 # @param {type:"number",placeholder:"1.0"}
D_max = 1.0 # @param {type:"number",placeholder:"1.0"}
P = 0.09 # @param {type:"slider",min:0,max:1,step:0.01}
I = 0.91 # @param {type:"slider",min:0,max:1,step:0.01}
D = 0 # @param {type:"slider",min:0,max:1,step:0.01}
engee.set_param!("pid_manual_tuning/ПИД-регулятор", "P"=>P*P_max, "I"=>I*I_max, "D"=>D*D_max)
engee.set_param!("pid_manual_tuning", "StopTime"=>StopTime)
# Запусти модель и получим результаты
data = engee.run("pid_manual_tuning")
x = collect(data["x"])
y = collect(data["y"])
# Удалим последний элемент если список переполнился
pushfirst!(all_runs, y)
if length(all_runs) > 5 pop!(all_runs); end;
# Анализ последнего переходного процесса
if length(all_runs) > 0
last_run = all_runs[1]
time_data = last_run.time
value_data = last_run.value
# Определяем установившееся значение (последние 10% данных)
steady_state_idx = Int.(collect((round(0.9 * length(value_data)):length(value_data))))
steady_state_value = mean(value_data[steady_state_idx])
# Определяем начальное значение
initial_value = value_data[1]
# Целевое значение (берем из задания)
target_value = x.value[end] # предполагая, что x - это задание
# Находим максимальное отклонение (перерегулирование)
max_overshoot = maximum(value_data)
overshoot_percentage = abs((max_overshoot - steady_state_value) / (target_value - initial_value)) * 100
# Время установления (5%)
tolerance = 0.05 * abs(target_value - initial_value)
settling_time = nothing
for i in length(value_data):-1:1
if abs(value_data[i] - steady_state_value) > tolerance
settling_time = time_data[i]
break
end
end
# Время нарастания (10%-90%)
rise_time_10 = nothing
rise_time_90 = nothing
threshold_10 = initial_value + 0.1 * (steady_state_value - initial_value)
threshold_90 = initial_value + 0.9 * (steady_state_value - initial_value)
for i in 1:length(value_data)
if value_data[i] >= threshold_10 && rise_time_10 === nothing
rise_time_10 = time_data[i]
end
if value_data[i] >= threshold_90 && rise_time_90 === nothing
rise_time_90 = time_data[i]
break
end
end
rise_time = rise_time_90 - rise_time_10
# Выводим результаты анализа
println("═"^50)
println("АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА")
println("═"^50)
println("Установившееся значение: $(round(steady_state_value, digits=3))")
println("Перерегулирование: $(round(overshoot_percentage, digits=1))%")
if settling_time !== nothing
println("Время установления (5%): $(round(settling_time, digits=2)) с")
else
println("Время установления: процесс не установился")
end
if rise_time !== nothing && rise_time_10 !== nothing
println("Время нарастания (10%-90%): $(round(rise_time, digits=2)) с")
end
# Статическая ошибка (если есть)
static_error = abs(target_value - steady_state_value)
if static_error > 1e-6
println("Статическая ошибка: $(round(static_error, digits=4))")
else
println("Статическая ошибка: отсутствует")
end
# Количество колебаний
peaks = 0
for i in 2:length(value_data)-1
if value_data[i] > value_data[i-1] && value_data[i] > value_data[i+1] &&
value_data[i] > steady_state_value
peaks += 1
end
end
println("Количество колебаний: $peaks")
println("═"^50)
end
# Выведем графики
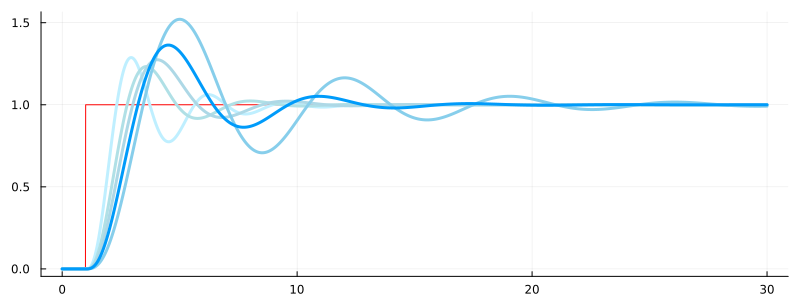
plot(x.time, x.value, c=:red, lw=1, size=(800,300), leg=false)
for i in length(all_runs):-1:1
plot!(all_runs[i].time, all_runs[i].value, c=colors[i], lw=3)
end
plot!()
Как это работает
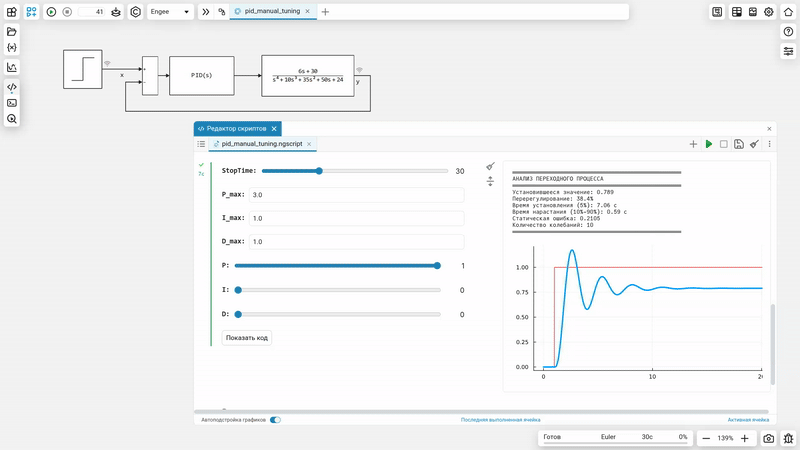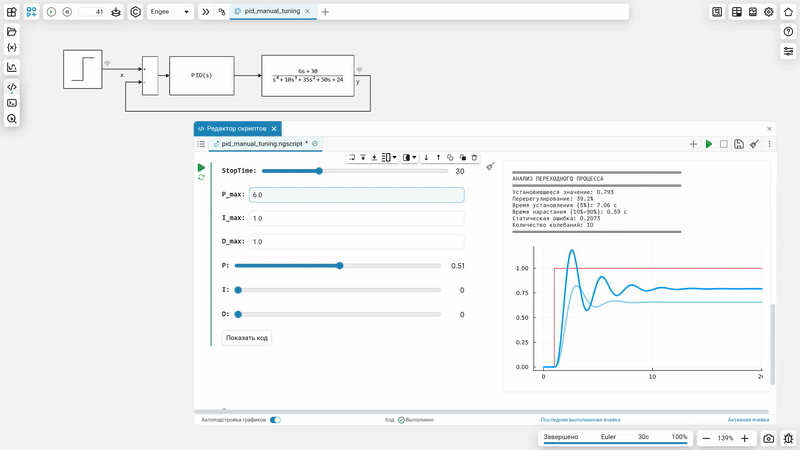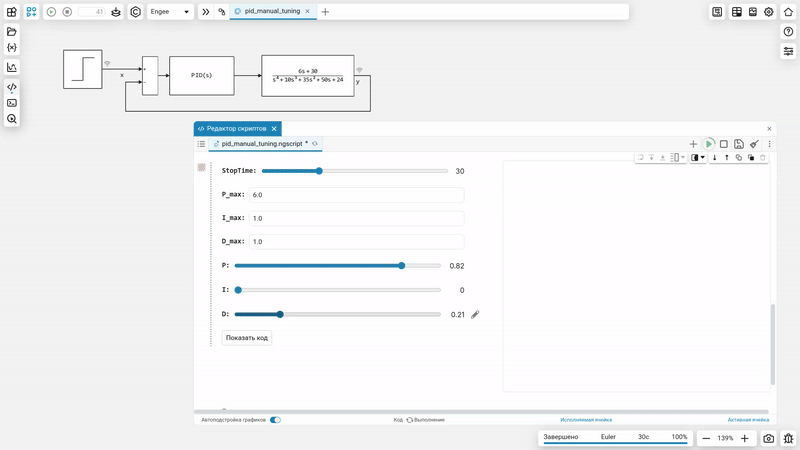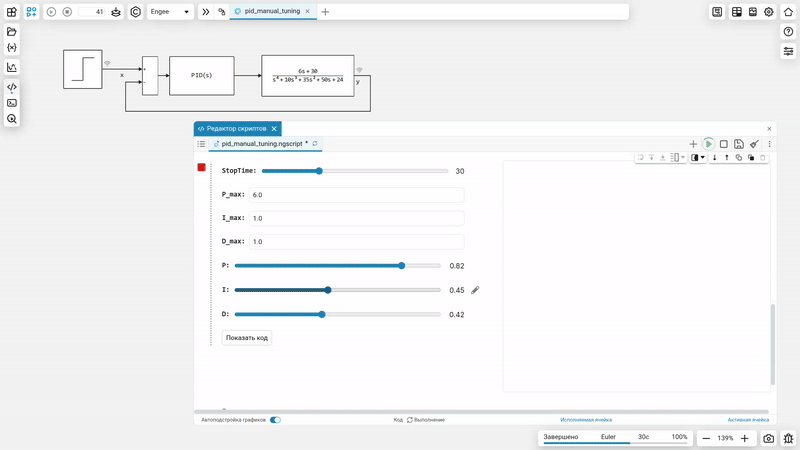
Заключение
Мы реализовали сравнительно огрубленный метод ручного подбора коэффициентов, который позволит настроить параметры для нелинейной, физической, линейной или линеаризованной системы. Наиболее цитируемым является метод подбора коэффициентов Циглера-Никольса, его и можно было бы реализовать при помощи созданного нами окружения.