Сравнительный анализ фильтров

В данном примере представлена модель фильтрации синусоиды, зашумлённой при помощи различных методов фильтрации с целью дальнейшего их сравнения.

Исходные данные:

1. Частота синусоиды (центральная частота сигнала): 100 кГц.
2. Мощность шума: 10^−7.

Sample_Time = 10^-6
Signal_Amplitude = 1
Сenter_frequency = 628318.5 # рад/с
Noise_power = 10^-7;

Расчётные данные:

1. Passband Edge Frequency (граница полосы пропускания) указывает пределы частот, в пределах которых сигнал проходит с минимальными искажениями. Для синусоидального сигнала с центральной частотой 100 кГц выбирается диапазон вокруг этой частоты.
2. Upper Passband Edge Frequency (граница верхней полосы пропускания) устанавливается чуть выше центральной частоты, чтобы сигнал прошёл с минимальными искажениями, примерно на 10% выше центральной частоты.
3. Passband Ripple (Рябь в полосе пропускания) определяет допустимое изменение амплитуды в полосе пропускания. Для высокоточных систем связи выбирается значение около 0.01–0.1 дБ.
4. Stopband Attenuation (затухание в полосе заграждения) указывает уровень подавления шума в полосе заграждения. Для нашего шума, чтобы его влияние стало незначительным, затухание должно быть не менее 60 дБ.

Эти значения являются ориентировочными и могут уточняться в зависимости от требований к сигналу, типа фильтра и особенностей реализации.

Далее мы зададим костанты для инициализации различных вариаций блока Analog Filter Design, но перед этим проанализируем ключевые параметры данного блока.

Analog Filter Design

Методы проектирования фильтров следующие.

1. Butterworth — амплитудно-частотная характеристика фильтра Баттерворта имеет максимально плоскую полосу пропускания и в целом монотонна.
2. Chebyshev I — амплитудно-частотная характеристика фильтра Чебышева I рода имеет равномерные пульсации в полосе пропускания и монотонна в полосе задерживания.
3. Chebyshev II — амплитудно-частотная характеристика фильтра Чебышева II рода монотонна в полосе пропускания и имеет равномерные пульсации в полосе задерживания.
4. Elliptic — амплитудно-частотная характеристика эллиптического фильтра имеет равномерные пульсации как в полосе пропускания, так и в полосе задерживания.
5. Bessel — амплитудно-частотная характеристика фильтра Бесселя имеет максимально плоскую полосу пропускания и в целом монотонна. Фильтр имеет максимально плоскую линейную фазово-частотную характеристику.

Тип частотной характеристики:

1. Lowpass — фильтр низких частот.
2. Highpass — фильтр высоких частот.
3. Bandpass — полосовой фильтр.
4. Bandstop — режекторный фильтр.

Lower_Frequency = 565486.65
Upper_frequency = 691150.35
Passband_ripple = 0.1
Stopband_attenuation = 60;

Discrete Filter

Далее зададим параметры блоков Discrete Filter. Этот блок независимо фильтрует каждый канал входного сигнала с заданным цифровым БИХ-фильтром.

Анализируя сам блок, стоит отметить, что он может реализовывать несколько структур фильтров.

Direct Form I (Прямая форма I).

Особенности. Использует два отдельных каскада: один для реализации полинома числителя (feedforward, 𝑏) и второй для полинома знаменателя (feedback, 𝑎). Включает две цепочки задержек: одну для входного сигнала и другую для выходного.

Преимущества. Простота концепции, что делает её удобной для анализа и проектирования.

Недостатки.

1. Большое количество регистров задержки.
2. Меньшая численная стабильность при реализации фильтров высокого порядка.

Direct Form II (Прямая форма II):

Особенности. Оптимизированная версия Direct Form I. Объединяет регистры задержки для полиномов числителя и знаменателя, что уменьшает требуемую память.

Преимущества. Экономия памяти за счёт уменьшения числа регистров.

Недостатки. Повышенная численная неустойчивость при реализации высоких порядков фильтра.

Direct Form I Transposed (Транспонированная форма I).

Особенности. Получена из Direct Form I путём транспонирования структуры. Потоки данных инверсируются: выход становится входом, а накопление значений изменяется на распределение.

Преимущества.

1. В некоторых случаях обладает улучшенными свойствами численной устойчивости.
2. Более удобна для реализации в некоторых аппаратных архитектурах.

Недостатки. Аналогична оригинальной Direct Form I с точки зрения общего числа регистров.

Direct Form II Transposed (Транспонированная форма II).

Особенности. Получена путем транспонирования Direct Form II.

Преимущества.

1. Часто имеет лучшую численную устойчивость, чем стандартная Direct Form II.
2. Удобна для реализации в цифровых сигнальных процессорах (DSP).

Недостатки. Также подвержена численной неустойчивости для фильтров высокого порядка, но в меньшей степени.

Таблица сравнения:

Характеристика	Direct Form I	Direct Form II	Direct Form I Transposed	Direct Form II Transposed
Число регистров задержки	(N + M - 2)	(\max(N, M) - 1)	(N + M - 2)	(\max(N, M) - 1)
Численная устойчивость	Средняя	Низкая	Средняя	Выше, чем в Direct Form II
Потребление памяти	Высокое	Низкое	Высокое	Низкое
Простота реализации	Высокая	Средняя	Средняя	Высокая
Аппаратная совместимость	Универсальная	Универсальная	Удобна для DSP	Оптимальна для DSP

Вывод:

1. Direct Form II и Direct Form II Transposed подходят для систем с ограниченными ресурсами памяти.
2. Direct Form I предпочтительна для фильтров низкого порядка из-за численной устойчивости.
3. Transposed Forms часто более устойчивы к численным ошибкам, что делает их полезными для высокопроизводительных приложений.

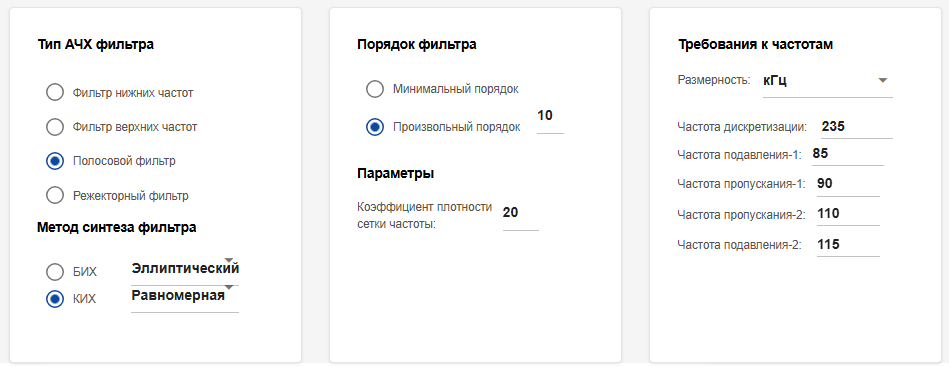
Далее для расчёта коэффициентов фильтра воспользуемся приложением «Редактор цифровых фильтров»

Метод проектирования фильтров будем задавать каждый раз различный. Далее посмотрим расчёты коэффициентов для каждого из фильтров. Перед этим переведём ранее рассчитанные значения граничных частот в Гц из рад/c b и округлим значения до целого числа, а также найдём частоту дискретизации сигнала. Согласно теореме Найквиста, частота дискретизации должна быть как минимум в два раза больше, чем максимальная частота сигнала, чтобы избежать алиасинга, также стоит учесть запас под верхнюю границу.

Алиасинг — это явление, возникающее при дискретизации аналогового сигнала, когда частота дискретизации недостаточна для корректного представления сигнала в цифровом виде. Это приводит к искажению сигнала, так как высокочастотные компоненты сигналов могут «сливаться» с более низкими частотами, создавая ложные частоты, которые не присутствуют в исходном сигнале.

Fcentr=round((Сenter_frequency/2π)/1000*2.3)
Flow=round((Lower_Frequency/2π)/1000)
Fup=round((Upper_frequency/2π)/1000)

println("Частота дискретизации: $(Fcentr) кГц")
println("Нижняя граничная частота: $(Flow) кГц")
println("Верхняя граничная частота: $(Fup) кГц")

Частота дискретизации: 230.0 кГц
Нижняя граничная частота: 90.0 кГц
Верхняя граничная частота: 110.0 кГц

Ниже приведён пример генерации коэффициентов для одного из фильтров. После генерации выполняем скачивание файлов и впоследствии используем их для определения фильтров.

Выгрузим коэффициенты из сгенерированных TXT-файлов, объявив функцию парсинга.

function read_coeff(path)
    # Читаем TXT
    txt = open(io->read(io, String), path)
    # Заменяем \n на запятые и оборачиваем строку в []
    data_str = "[" * replace(txt, "\n" => ",") * "]"
    # Преобразуем строку в выражение
    parsed_expr = Meta.parse(data_str)
    # Выполняем выражение, чтобы получить вектор
    data_vector = eval(parsed_expr)
    return data_vector
end

read_coeff (generic function with 1 method)

# Чтение числителя и знаменателя Баттерворта
bat_num = read_coeff("$(@__DIR__)/coefficients/IIR_num_1.txt")
bat_denum = read_coeff("$(@__DIR__)/coefficients/IIR_denum_1.txt")
# Чтение числителя и знаменателя Чебышева 1
che1_num = read_coeff("$(@__DIR__)/coefficients/IIR_num_1.txt")
che1_denum = read_coeff("$(@__DIR__)/coefficients/IIR_denum_1.txt")
# Чтение числителя и знаменателя Чебышева 2
che2_num = read_coeff("$(@__DIR__)/coefficients/IIR_num_1.txt")
che2_denum = read_coeff("$(@__DIR__)/coefficients/IIR_denum_1.txt")
# Чтение числителя и эллиптического знаменателя
elp_num = read_coeff("$(@__DIR__)/coefficients/IIR_num_1.txt")
elp_denum = read_coeff("$(@__DIR__)/coefficients/IIR_denum_1.txt");

First-Order Filter

Следующий фильтр, который мы рассмотрим в этой демонстрации, – это First-Order Filter. Данный блок реализует простой фильтр верхних или нижних частот. Зададим его параметры при условии, что частота среза составляет 120 кГц.

Fc = 120 # Частота среза
τ=1/2π*Fc; # Постоянная времени фильтра

Discrete FIR Filter

Далее рассмотрим блок Discrete FIR Filter. Для его реализации также воспользуемся приложением «Редактор цифровых фильтров» и ранее описанной функцией парсинга коэффициентов.

Для задания дополнительных частот обявим интервальные частоты с интервалом +-15%, дабы они оказались за границами ранее описанного диапазона в +-10%.

println("Новая частота дискретизации: $(Fcentr+5) кГц")
println("Вторая нижняя граничная частота: $(Flow-5) кГц")
println("Вторая верхняя граничная частота: $(Fup+5) кГц")

Новая частота дискретизации: 235.0 кГц
Вторая нижняя граничная частота: 85.0 кГц
Вторая верхняя граничная частота: 115.0 кГц

fir_num = read_coeff("$(@__DIR__)/coefficients/fir_num.txt")

Median Filter

Далее мы рассмотрим самый простой блок в этой демонстрации – Median Filter.

Блок Median Filter вычисляет скользящую медиану входного сигнала по каждому каналу независимо с течением времени. Блок использует метод скользящего окна, и единственный параметр, который мы можем регулировать, – это само окно фильтрации.

window = 15;

Notch-Peak Filter

Последний блок, который мы рассмотрим, – Notch-Peak Filter. Он фильтрует каждый канал входного сигнала по времени, используя заданную центральную частоту и полосу пропускания 3 дБ. Этот блок предлагает настраиваемые параметры проекта фильтра, которые позволяют назначать характеристики фильтра во время выполнения моделирования.

Рассчитаем параметры при условии, что Q (коэффициент добротности) = 10.

Sample_rate = 1/Sample_Time 
Q = 10;
Fs=round((Сenter_frequency/2π))
BW = Fs/Q

println("Ширина полосы при Q=10: $(BW/1000) кГц")
println("Центральная частота сигнала: $(Fs/1000) кГц")
println("Частота дискретизации: $(Sample_rate/1e6) МГц")

Ширина полосы при Q=10: 10.0 кГц
Центральная частота сигнала: 100.0 кГц
Частота дискретизации: 1.0 МГц

Перед началом моделирования ещё раз убедимся, что все необходимые переменные объявлены.

# Получаем список всех переменных в рабочей области
vars = names(Main, all=true)

# Выводим массивы и скаляры
for var in vars
    value = getfield(Main, var)
    if isa(value, AbstractArray)
        println("Массив: ", var, ", Размер: ", size(value))
    elseif isa(value, Number) || isa(value, String)
        println("Скаляр: ", var, ", Значение: ", value)
    end
end

Скаляр: BW, Значение: 10000.0
Скаляр: Fc, Значение: 120
Скаляр: Fcentr, Значение: 230.0
Скаляр: Flow, Значение: 90.0
Скаляр: Fs, Значение: 100000.0
Скаляр: Fup, Значение: 110.0
Скаляр: Lower_Frequency, Значение: 565486.65
Скаляр: Magnitude, Значение: 1
Скаляр: Noise_power, Значение: 1.0000000000000001e-7
Скаляр: Passband_ripple, Значение: 0.1
Скаляр: Phase, Значение: 0
Скаляр: Q, Значение: 10
Скаляр: Sample_Time, Значение: 1.0e-6
Скаляр: Sample_rate, Значение: 1.0e6
Скаляр: Signal_Amplitude, Значение: 1
Скаляр: Stopband_attenuation, Значение: 60
Скаляр: Upper_frequency, Значение: 691150.35
Массив: bat_denum, Размер: (21,)
Массив: bat_num, Размер: (21,)
Массив: che1_denum, Размер: (21,)
Массив: che1_num, Размер: (21,)
Массив: che2_denum, Размер: (21,)
Массив: che2_num, Размер: (21,)
Скаляр: data_str, Значение: [1.0,15.726465174717665,118.19779715124804,564.5945977782826,1922.5628210505968,4961.486649014338,10069.27911225147,16457.781390988064,22003.338138220104,24301.413576125095,22293.787678765948,17018.378514886626,10791.5437594143,5653.533013094259,2423.11034196715,836.6005210914026,227.22904721973316,46.794190857389,6.873719057490497,0.6421978090261691,0.028701721170992484]
Массив: data_vector, Размер: (21,)
Массив: elp_denum, Размер: (21,)
Массив: elp_num, Размер: (21,)
Массив: fir_denum, Размер: (11,)
Массив: fir_num, Размер: (11,)
Массив: preload_cells_startlog, Размер: (36,)
Скаляр: preloaded_cells_dir, Значение: /app/IJulia/preload_cells
Массив: preloaded_cells_names, Размер: (19,)
Скаляр: txt, Значение: 1.0
15.726465174717665
118.19779715124804
564.5945977782826
1922.5628210505968
4961.486649014338
10069.27911225147
16457.781390988064
22003.338138220104
24301.413576125095
22293.787678765948
17018.378514886626
10791.5437594143
5653.533013094259
2423.11034196715
836.6005210914026
227.22904721973316
46.794190857389
6.873719057490497
0.6421978090261691
0.028701721170992484
Массив: vars, Размер: (337,)
Скаляр: window, Значение: 15
Скаляр: τ, Значение: 19.098593171027442
Скаляр: Сenter_frequency, Значение: 628318.5

Запуск модели и анализ результатов

Теперь перейдём к тестированию построенной схемы и анализу различных видов фильтрации на основе спектральных характеристик сигнала до и после фильтрации. Сначала объявим функцию запуска модели и запустим модель, чтобы сохранить результаты моделирования в рабочую область Engee.

Запуск модели

# Подключение вспомогательной функции запуска модели.
function run_model( name_model)
    
    Path = (@__DIR__) * "/" * name_model * ".engee"
    
    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end
    sleep(5)
    return model_output
end

run_model("Comparative_analysis_of_filters")

SimulationResult(
    "Analog Filter Design-11.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-11.1"),
    "Discrete Filter-3.1" => WorkspaceArray("Comparative_analysis_of_filters/Discrete Filter-3.1"),
    "inpNoise" => WorkspaceArray("Comparative_analysis_of_filters/inpNoise"),
    "Analog Filter Design-14.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-14.1"),
    "First-Order Filter-1.Out" => WorkspaceArray("Comparative_analysis_of_filters/First-Order Filter-1.Out"),
    "Analog Filter Design-4.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-4.1"),
    "Discrete Filter-2.1" => WorkspaceArray("Comparative_analysis_of_filters/Discrete Filter-2.1"),
    "Analog Filter Design.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design.1"),
    "Analog Filter Design-16.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-16.1"),
    "Analog Filter Design-15.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-15.1"),
    "Analog Filter Design-13.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-13.1"),
    "Analog Filter Design-1.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-1.1"),
    "Median Filter.1" => WorkspaceArray("Comparative_analysis_of_filters/Median Filter.1"),
    "Analog Filter Design-19.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-19.1"),
    "Analog Filter Design-7.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-7.1"),
    "Discrete Filter-1.1" => WorkspaceArray("Comparative_analysis_of_filters/Discrete Filter-1.1"),
    "Analog Filter Design-2.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-2.1"),
    "Analog Filter Design-10.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-10.1"),
    "Analog Filter Design-9.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-9.1"),
    "Discrete Filter.1" => WorkspaceArray("Comparative_analysis_of_filters/Discrete Filter.1"),
    "Analog Filter Design-18.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-18.1"),
    "inp" => WorkspaceArray("Comparative_analysis_of_filters/inp"),
    "Notch-Peak Filter.1" => WorkspaceArray("Comparative_analysis_of_filters/Notch-Peak Filter.1"),
    "Analog Filter Design-17.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-17.1"),
    "Analog Filter Design-12.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-12.1"),
    "Analog Filter Design-3.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-3.1"),
    "Analog Filter Design-6.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-6.1"),
    "First-Order Filter.Out" => WorkspaceArray("Comparative_analysis_of_filters/First-Order Filter.Out"),
    "Analog Filter Design-8.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-8.1"),
    "Analog Filter Design-5.1" => WorkspaceArray("Comparative_analysis_of_filters/Analog Filter Design-5.1")
)

Анализ результатов

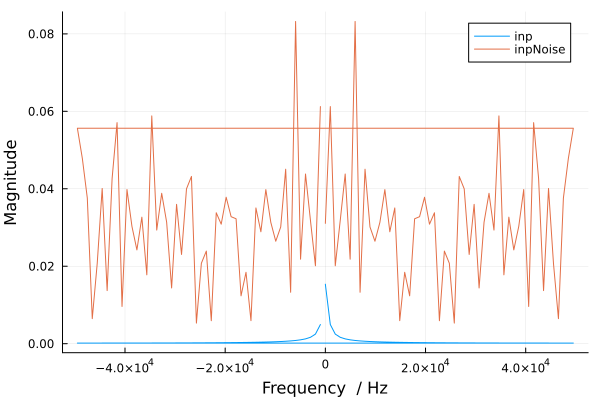
Начнём с построения спектра исходного сигнала.

using FFTW
gr()

Plots.GRBackend()

inp = collect(simout["Comparative_analysis_of_filters/inp"]);
inp = inp.value;
inpNoise = collect(simout["Comparative_analysis_of_filters/inpNoise"]);
inpNoise = inpNoise.value;

plot(fftfreq(length(inp), Fs), abs.(fft(inp)./length(inp)), 
        label = "inp" , xguide="Frequency  / Hz", yguide="Magnitude")
plot!(fftfreq(length(inpNoise), Fs), abs.(fft(inpNoise)./length(inpNoise)), 
        label = "inpNoise" , xguide="Frequency  / Hz", yguide="Magnitude")

Из спектра зашумлённого сигнала явно видны основные частоты сигнала, а именно 100 кГц.

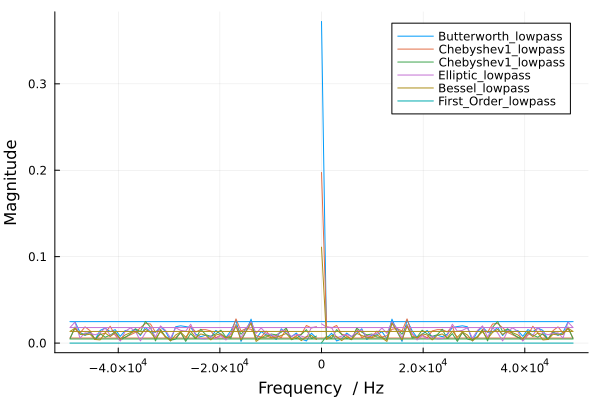
Далее сравним все фильтры низких частот.

Butterworth_lowpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design.1"]);
Butterworth_lowpass = Butterworth_lowpass.value;
plot(fftfreq(length(Butterworth_lowpass), Fs), abs.(fft(Butterworth_lowpass)./length(Butterworth_lowpass)), 
        label = "Butterworth_lowpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev1_lowpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-4.1"]);
Chebyshev1_lowpass = Chebyshev1_lowpass.value;
plot!(fftfreq(length(Chebyshev1_lowpass), Fs), abs.(fft(Chebyshev1_lowpass)./length(Chebyshev1_lowpass)), 
        label = "Chebyshev1_lowpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev2_lowpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-8.1"]);
Chebyshev2_lowpass = Chebyshev2_lowpass.value;
plot!(fftfreq(length(Chebyshev2_lowpass), Fs), abs.(fft(Chebyshev2_lowpass)./length(Chebyshev2_lowpass)), 
        label = "Chebyshev1_lowpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Elliptic_lowpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-12.1"]);
Elliptic_lowpass = Elliptic_lowpass.value;
plot!(fftfreq(length(Elliptic_lowpass), Fs), abs.(fft(Elliptic_lowpass)./length(Elliptic_lowpass)), 
        label = "Elliptic_lowpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Bessel_lowpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-16.1"]);
Bessel_lowpass = Bessel_lowpass.value;
plot!(fftfreq(length(Bessel_lowpass), Fs), abs.(fft(Bessel_lowpass)./length(Bessel_lowpass)), 
        label = "Bessel_lowpass" , xguide="Frequency  / Hz", yguide="Magnitude")

First_Order_lowpass = collect(simout["Comparative_analysis_of_filters/First-Order Filter.Out"]);
First_Order_lowpass = First_Order_lowpass.value;
plot!(fftfreq(length(First_Order_lowpass), Fs), abs.(fft(First_Order_lowpass)./length(First_Order_lowpass)), 
        label = "First_Order_lowpass" , xguide="Frequency  / Hz", yguide="Magnitude")

В данном случае фильтры низких частот снизили амплитуду основной частоты сигнала, что привело к потере полезной информации. Это произошло по той причине, что фильтр пропускает только низкие частоты. Получилось, что частота в 100 кГц вырезана, и остались лишь компоненты с частотами, близкими к 0 Гц.

Фильтры низких частот (Low-pass filters) пропускают сигналы с частотами, которые находятся ниже определённого порога, называемого частотой среза. Все компоненты сигнала, частоты которых выше этого порога, будут подавляться. В данном случае фильтр срезал частоту 100 кГц, так как она превышала порог, оставив лишь очень низкие частоты (близкие к 0 Гц), которые ассоциируются с постоянной составляющей или медленно меняющимися сигналами. Это может привести к потере важной информации, если основной сигнал имеет высокую частоту, например, 100 кГц.

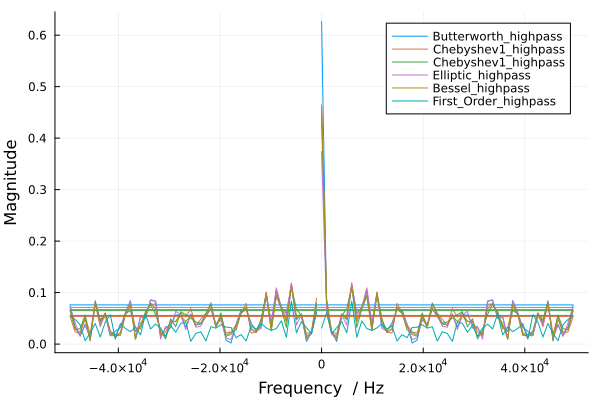
Перейдём к фильтрам высокой частоты.

Butterworth_highpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-1.1"]);
Butterworth_highpass = Butterworth_highpass.value;
plot(fftfreq(length(Butterworth_highpass), Fs), abs.(fft(Butterworth_highpass)./length(Butterworth_highpass)), 
        label = "Butterworth_highpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev1_highpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-5.1"]);
Chebyshev1_highpass = Chebyshev1_highpass.value;
plot!(fftfreq(length(Chebyshev1_highpass), Fs), abs.(fft(Chebyshev1_highpass)./length(Chebyshev1_highpass)), 
        label = "Chebyshev1_highpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev2_highpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-9.1"]);
Chebyshev2_highpass = Chebyshev2_highpass.value;
plot!(fftfreq(length(Chebyshev2_highpass), Fs), abs.(fft(Chebyshev2_highpass)./length(Chebyshev2_highpass)), 
        label = "Chebyshev1_highpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Elliptic_highpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-13.1"]);
Elliptic_highpass = Elliptic_highpass.value;
plot!(fftfreq(length(Elliptic_highpass), Fs), abs.(fft(Elliptic_highpass)./length(Elliptic_highpass)), 
        label = "Elliptic_highpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Bessel_highpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-17.1"]);
Bessel_highpass = Bessel_highpass.value;
plot!(fftfreq(length(Bessel_highpass), Fs), abs.(fft(Bessel_highpass)./length(Bessel_highpass)), 
        label = "Bessel_highpass" , xguide="Frequency  / Hz", yguide="Magnitude")

First_Order_highpass = collect(simout["Comparative_analysis_of_filters/First-Order Filter-1.Out"]);
First_Order_highpass = First_Order_highpass.value;
plot!(fftfreq(length(First_Order_highpass), Fs), abs.(fft(First_Order_highpass)./length(First_Order_highpass)), 
        label = "First_Order_highpass" , xguide="Frequency  / Hz", yguide="Magnitude")

В данном случае фильтры высоких частот (High-pass filters) не смогли эффективно подавить компоненты сигнала на частотах ниже 100 кГц, в результате чего оставались искажения. Несмотря на то, что амплитуда на частоте 0 Гц выше, чем на 100 кГц, фильтр пропустил все частоты, превышающие порог среза. Кроме того, на графике видны ещё два пика с меньшей амплитудой, чем у 100 кГц, но эти пики всё равно оставались ярко выраженными.

Фильтры высоких частот пропускают сигналы с частотами, которые превышают заданную частоту среза. Компоненты сигнала с частотами ниже этой границы будут подавляться. В данном случае фильтр срезал частоты ниже 100 кГц, однако оставшиеся пики на графике, даже если их амплитуда была ниже 100 кГц, могли быть достаточно выраженными из-за нескольких причин, которые обсудим ниже.

Шум или помехи. Сигнал мог содержать шум или гармоники, которые находятся в диапазоне между срезом фильтра и частотой 100 кГц. Эти пики могут быть вызваны внешними помехами или другими частотными компонентами, которые не были полностью подавлены фильтром.

1. Резонансные частоты системы. В некоторых случаях система может иметь резонансные частоты, где амплитуда сигнала усиливается. Даже если эти пики имеют меньшую амплитуду по сравнению с основной частотой, они могут оставаться выраженными, если совпадают с резонансными частотами или особенностями спектра сигнала.

2. Пограничные эффекты фильтра. Сам фильтр может быть не идеален, и на границе среза может происходить «полупроницаемость» для частот, которые близки к частоте среза, что позволяет оставить некоторые пики, даже если они находятся в диапазоне частот, который должен был бы быть подавлен.

Таким образом, фильтр высоких частот пропустил частоты выше 100 кГц, оставив амплитудные пики, которые могли быть вызваны другими эффектами или особенностями сигнала.

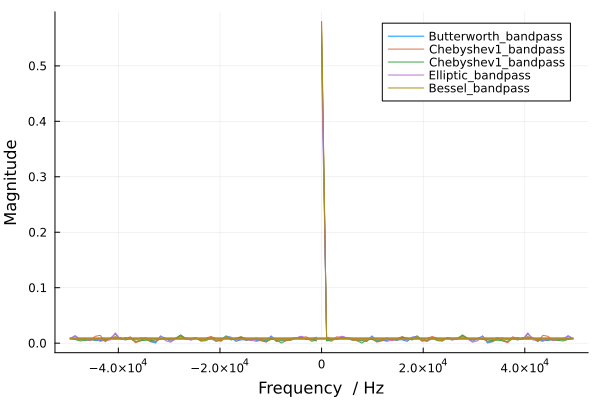
Расмотрим фильтры полосы заграждения.

Butterworth_bandpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-2.1"]);
Butterworth_bandpass = Butterworth_bandpass.value;
plot(fftfreq(length(Butterworth_bandpass), Fs), abs.(fft(Butterworth_bandpass)./length(Butterworth_bandpass)), 
        label = "Butterworth_bandpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev1_bandpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-6.1"]);
Chebyshev1_bandpass = Chebyshev1_bandpass.value;
plot!(fftfreq(length(Chebyshev1_bandpass), Fs), abs.(fft(Chebyshev1_bandpass)./length(Chebyshev1_bandpass)), 
        label = "Chebyshev1_bandpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev2_bandpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-10.1"]);
Chebyshev2_bandpass = Chebyshev2_bandpass.value;
plot!(fftfreq(length(Chebyshev2_bandpass), Fs), abs.(fft(Chebyshev2_bandpass)./length(Chebyshev2_bandpass)), 
        label = "Chebyshev1_bandpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Elliptic_bandpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-14.1"]);
Elliptic_bandpass = Elliptic_bandpass.value;
plot!(fftfreq(length(Elliptic_bandpass), Fs), abs.(fft(Elliptic_bandpass)./length(Elliptic_bandpass)), 
        label = "Elliptic_bandpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Bessel_bandpass = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-18.1"]);
Bessel_bandpass = Bessel_bandpass.value;
plot!(fftfreq(length(Bessel_bandpass), Fs), abs.(fft(Bessel_bandpass)./length(Bessel_bandpass)), 
        label = "Bessel_bandpass" , xguide="Frequency  / Hz", yguide="Magnitude")

Эти фильтры также имеют наибольшую амплитуду сигнала при 0 Гц, в то время, как все остальные частоты, включая полезную для нас частоту 100 МГц, практически полностью подавлены.

Фильтры полосы заграждения предназначены для подавления определённого диапазона частот, оставляя всё, что находится за пределами этого диапазона. В данном случае фильтр эффективно блокирует частоты, включая 100 МГц, что является важным для нас сигналом. Однако при этом фильтр пропускает сигналы только на частотах, близких к 0 Гц, то есть низкочастотные компоненты (например, постоянное напряжение). Все другие частоты, как полезные, так и шумовые, в пределах заграждённой полосы подавляются. Это может привести к потере полезной информации, если сигнал имеет частоту, попадающую в диапазон заграждения фильтра, как это произошло с 100 МГц.

Расмотрим фильтры полосы пропускания.

Butterworth_bandstop = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-3.1"]);
Butterworth_bandstop = Butterworth_bandstop.value;
plot(fftfreq(length(Butterworth_bandstop), Fs), abs.(fft(Butterworth_bandstop)./length(Butterworth_bandstop)), 
        label = "Butterworth_bandstop" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev1_bandstop = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-7.1"]);
Chebyshev1_bandstop = Chebyshev1_bandstop.value;
plot!(fftfreq(length(Chebyshev1_bandstop), Fs), abs.(fft(Chebyshev1_bandstop)./length(Chebyshev1_bandstop)), 
        label = "Chebyshev1_bandstop" , xguide="Frequency  / Hz", yguide="Magnitude")

Chebyshev2_bandstop = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-11.1"]);
Chebyshev2_bandstop = Chebyshev2_bandstop.value;
plot!(fftfreq(length(Chebyshev2_bandstop), Fs), abs.(fft(Chebyshev2_bandstop)./length(Chebyshev2_bandstop)), 
        label = "Chebyshev1_bandstop" , xguide="Frequency  / Hz", yguide="Magnitude")

Elliptic_bandstop = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-15.1"]);
Elliptic_bandstop = Elliptic_bandstop.value;
plot!(fftfreq(length(Elliptic_bandstop), Fs), abs.(fft(Elliptic_bandstop)./length(Elliptic_bandstop)), 
        label = "Elliptic_bandstop" , xguide="Frequency  / Hz", yguide="Magnitude")

Bessel_bandstop = collect(simout["Comparative_analysis_of_filters/Analog Filter Design-19.1"]);
Bessel_bandstop = Bessel_bandstop.value;
plot!(fftfreq(length(Bessel_bandstop), Fs), abs.(fft(Bessel_bandstop)./length(Bessel_bandstop)), 
        label = "Bessel_bandstop" , xguide="Frequency  / Hz", yguide="Magnitude")

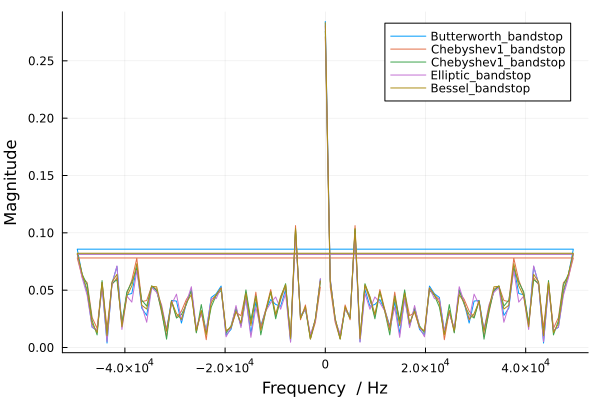
Фильтры полосы пропускания показали лучшие результаты по сравнению с предыдущими, так как на графике ярко выделяются три пика: самый высокий на 0 Гц и два более низких — на 100 кГц и -100 кГц.

Фильтры полосы пропускания (Band-pass filters) позволяют пройти только сигналам в определённом диапазоне частот, пропуская их в пределах заданной полосы и подавляя все остальные. В данном случае фильтр оставил три основных пика: первый пик на 0 Гц, который может быть связан с постоянной составляющей или низкочастотным компонентом сигнала, а два других пика — на 100 кГц и -100 кГц, которые представляют собой полезные высокочастотные компоненты. Эти пики чётко видны, потому что фильтр позволил пройти частотам в пределах полосы пропускания, эффективно исключив всё остальное.

Далее перейдём к анализу блоков Discrete Filter.

Discrete_Butterworth = collect(simout["Comparative_analysis_of_filters/Discrete Filter-2.1"]);
Discrete_Butterworth = Discrete_Butterworth.value;
plot(fftfreq(length(Discrete_Butterworth), Fs), abs.(fft(Discrete_Butterworth)./length(Discrete_Butterworth)), 
        label = "Discrete_Butterworth" , xguide="Frequency  / Hz", yguide="Magnitude")

Discrete_Chebyshev1 = collect(simout["Comparative_analysis_of_filters/Discrete Filter-3.1"]);
Discrete_Chebyshev1 = Discrete_Chebyshev1.value;
plot!(fftfreq(length(Discrete_Chebyshev1), Fs), abs.(fft(Discrete_Chebyshev1)./length(Discrete_Chebyshev1)), 
        label = "Discrete_Chebyshev1" , xguide="Frequency  / Hz", yguide="Magnitude")

Discrete_Chebyshev2 = collect(simout["Comparative_analysis_of_filters/Discrete Filter-1.1"]);
Discrete_Chebyshev2 = Discrete_Chebyshev2.value;
plot!(fftfreq(length(Discrete_Chebyshev2), Fs), abs.(fft(Discrete_Chebyshev2)./length(Discrete_Chebyshev2)), 
        label = "Discrete_Chebyshev2" , xguide="Frequency  / Hz", yguide="Magnitude")

Discrete_Elliptic = collect(simout["Comparative_analysis_of_filters/Discrete Filter.1"]);
Discrete_Elliptic = Discrete_Elliptic.value;
plot!(fftfreq(length(Discrete_Elliptic), Fs), abs.(fft(Discrete_Elliptic)./length(Discrete_Elliptic)), 
        label = "Discrete_Elliptic" , xguide="Frequency  / Hz", yguide="Magnitude")

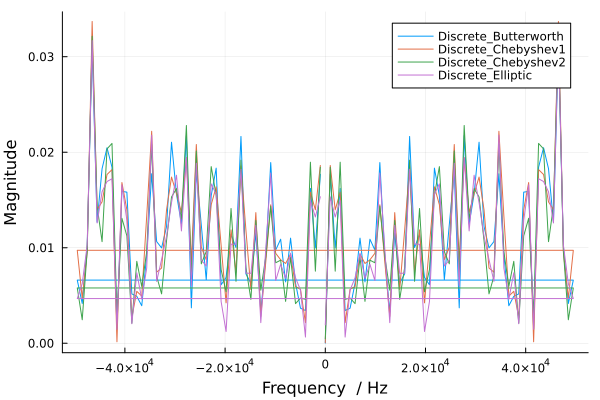
Теперь перейдём к анализу блоков дискретных фильтров: Discrete_Butterworth, Discrete_Chebyshev1, Discrete_Chebyshev2 и Discrete_Elliptic. Эти фильтры показали худшие результаты на данный момент, что, вероятно, связано с некорректно заданными коэффициентами фильтрации. На графике ярко выражен пик на частоте 46 кГц, в то время, как все остальные пики расположены на примерно одинаковом уровне.

Дискретные фильтры, такие как Butterworth, Chebyshev и Elliptic, имеют свои особенности в плане частотной характеристики. Однако, если коэффициенты фильтрации заданы некорректно, они могут неэффективно справляться с задачей фильтрации, что приводит к плохим результатам. В данном случае пик на 46 кГц был особенно выражен, что может означать, что фильтры не смогли должным образом подавить компоненты в этой частотной области. Остальные пики, расположенные на одном уровне, указывают на недостаточную селективность фильтров, что может быть связано с неправильным выбором параметров фильтрации, таких как частота среза или порядок фильтра.

Теперь проанализируем усредняющий фильтр.

Median_Filter = collect(simout["Comparative_analysis_of_filters/Median Filter.1"]);
Median_Filter = Median_Filter.value;
plot(fftfreq(length(Median_Filter), Fs), abs.(fft(Median_Filter)./length(Median_Filter)), 
        label = "Median_Filter" , xguide="Frequency  / Hz", yguide="Magnitude")

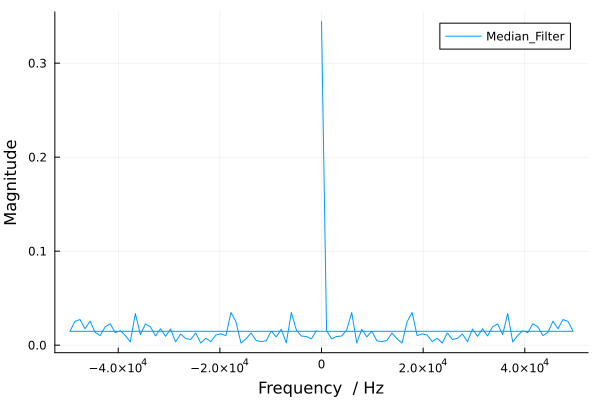
Усредняющий фильтр не справился с задачей, так как выбранный размер окна (15) оказался слишком большим для эффективного удаления помех. Просто этот фильтр плохо подходит для такой задачи. На графике также наблюдается яркий пик на 0 Гц.

Усредняющий фильтр работает путём сглаживания сигнала, что позволяет уменьшить случайные колебания, но при этом может быть неэффективным для удаления высокочастотных помех, особенно, если окно фильтра слишком велико. В данном случае размер окна 15 оказался слишком большим, что не позволило удалить помехи, особенно на высоких частотах. Кроме того, усредняющий фильтр не предназначен для точной фильтрации узкополосных или высокочастотных сигналов, что делает его не совсем подходящим для такой задачи. Яркий пик на 0 Гц может указывать на то, что фильтр не смог эффективно подавить постоянные или низкочастотные компоненты сигнала.

Далее проведём анализ КИХ-фильтра.

FIR = collect(simout["Comparative_analysis_of_filters/Discrete Filter-1.1"]);
FIR = FIR.value;
plot(fftfreq(length(FIR), Fs), abs.(fft(FIR)./length(FIR)), 
        label = "FIR" , xguide="Frequency  / Hz", yguide="Magnitude")

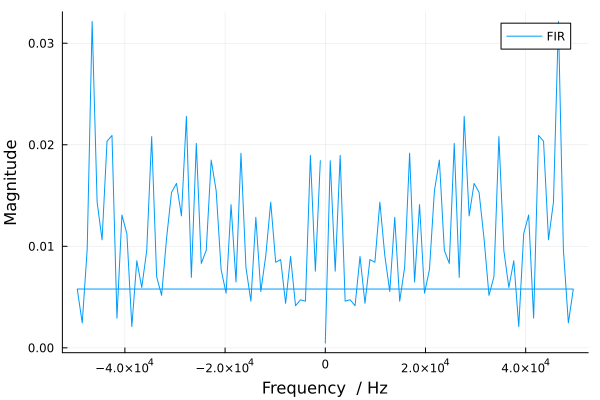
Для КИХ-фильтра справедливы выводы, сделанные выше для блока Discrete Filter.

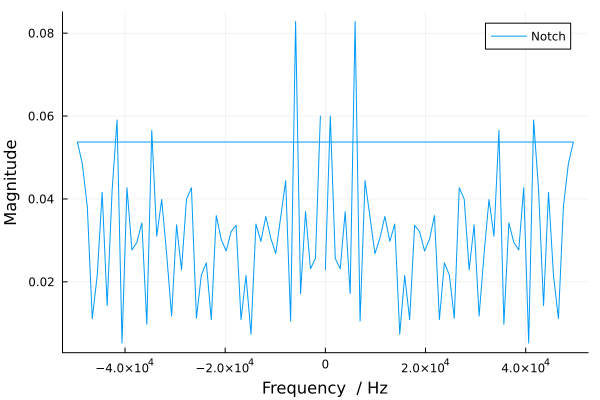
Теперь построим спектр для блока Notch-Peak Filter.

Notch = collect(simout["Comparative_analysis_of_filters/Notch-Peak Filter.1"]);
Notch = Notch.value;
plot(fftfreq(length(Notch), Fs), abs.(fft(Notch)./length(Notch)), 
        label = "Notch" , xguide="Frequency  / Hz", yguide="Magnitude")

Блок Notch-Peak Filter в данном эксперименте показал лучший результат.

Фильтр полосы заграждения с параметром Q=10 позволяет эффективно изолировать сигнал в полосе шириной 10.0 кГц около центральной частоты 100 кГц. При такой настройке фильтр способен выделить и усилить компоненты сигнала на частоте 100 кГц, что и видно на графике. Пик на 0 Гц, хоть и менее выражен, может указывать на наличие низкочастотных составляющих, например, постоянной компоненты сигнала. Несмотря на его небольшую амплитуду, фильтр эффективно убрал другие частоты, оставив только необходимые пики на 100 кГц.

Вывод

Мы рассмотрели фильтры для решения данной задачи и выяснили, что самый подходящий — это Notch-Peak Filter с параметром Q=10, который позволил сохранить полезные компоненты сигнала на 100 кГц при минимальной потере данных.

Большинство других фильтров не показали достаточной эффективности из-за некорректной настройки коэффициентов фильтрации или неправильного выбора типа фильтра для задачи. Желательно провести дополнительные эксперименты с настройкой параметров фильтров, особенно для дискретных фильтров и фильтров полосы пропускания, чтобы оптимизировать их работу для данной задачи.

Эта демонстрация доказала важность точной настройки фильтров и выбора подходящего типа фильтра для сохранения полезной информации в сигнале.