Стабилизация продуктовой метрики Удержание (Retention)
Решение задачи стабилизации продуктовой метрики Удержание (Retention)
Аннотация
В работе моделируются с использованием тензоров или многоиндексных объектов нелинейные системы управления с полиномиальными функциями пространства состояний. Вводится и используется новый бинарный оператор алгебры многоиндексных объектов и тензорной алгебры. Предлагается способ моделирования нелинейных систем управления с дискретным временем, основанный на описанном операторе тензорного умножения. Решается задача стабилизации процесса удержания подачей определенного управляющего сигнала в заданный момент времени.
Ключевые слова:
- нелинейные системы управления,
- системы автоматизированного управления,
- нелинейные процессы,
- многоиндексные объекты,
- тензоры,
- тензорное исчисление,
- тензорная алгебра,
- тензорное произведение.
Введение
Удержание (retention) - это продуктовая метрика, которая отражает процент пользователей, продолжающих использовать продукт или услугу после определенного периода времени. Этот показатель используется для оценки успешности продукта или услуги и их способности удерживать пользователей.
Данная работа демонстрирует моделирование процесса удержания и решает задачу его стабилизации.
Цель работы - сравнение результатов моделирования САУ с полиномиальными функциями пространства состояний в Engee и в Python с помощью предложенного оператора тензорного умножения (см. Минитаева А.М. Новый оператор тензорного произведения и анализ нелинейных систем с полиномиальными функциями пространства состояний // Информационно-технологический вестник. 2024. № 3.)
Задача - стабилизация когортной кривой удержания в произвольный момент времени.
Удержание и отток
Отток
Относительно удержания, отток (churn rate) - это продуктовая метрика, которая показывает процент пользователей, перестающих использовать продукт или услугу в течение определенного периода времени. Отток может быть вызван различными причинами, включая низкое качество продукта, высокую стоимость, отсутствие необходимой функциональности и т.д.
Удержание и отток являются важными показателями для компаний, так как они помогают определить, насколько успешно компания привлекает новых пользователей и удерживает уже существующих. Продуктовая метрика оттока (churn) очень важна для бизнеса, его цель - минимизация оттока.
Удержание
На графике ниже изображены три кривые удержания клиентов — синяя линия изображает ситуацию, когда у компании наблюдается 5%-ный отток клиентов в месяц, красная — когда в неделю отток клиентов уменьшается на 1%, оранжевая — на 2%:
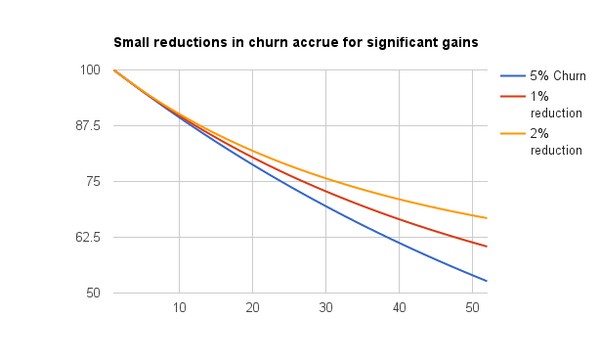
Для отслеживания оттока и его визуализации проще всего использовать когортную кривую удержания (retention cohort curve):
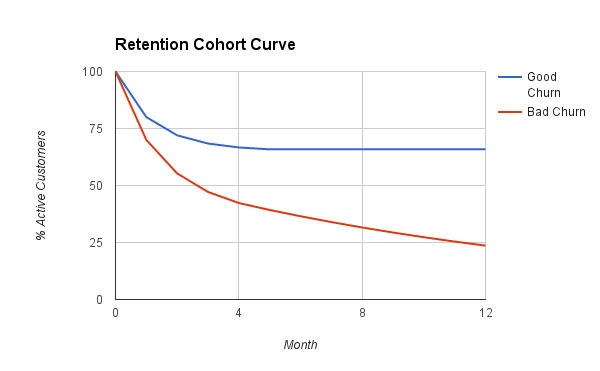
Внешний вид кривых напоминает обратно-пропорциональную зависимость от времени. Такие процессы характеризуются квадратичными функциями состояния.
Когортная кривая удержания
Система ДУ
Пример. Решим в Engee методом Эйлера систему ОДУ
при начальных условиях , на отрезке .
Разобьем отрезок на частей и реализуем алгоритм метода Эйлера, затем построим графики решения.
using Plots;
a = 0;
b = 6;
n = 1000;
h = (b - a) / n;
t = zeros(n+1);
func1 = zeros(n+1);
func2 = zeros(n+1);
x = zeros(n+1);
y = zeros(n+1);
t[1] = a;
x[1] = 1;
y[1] = 2;
for i in 1:n
t[i+1] = t[i] + h;
func1[i] = (-1)*x[i]*x[i];
x[i+1] = x[i] + h * func1[i];
func2[i] = (-1)*y[i]*y[i];
y[i+1] = y[i] + h * func2[i];
end
plot(t, y, label="x2(t)=y, x2(0)=2")
plot!(t, x, label="x1(t)=x, x1(0)=1")
plot!(t, x+ones(n+1), line =:dashdot, label="x1(t)=x+1, x1(0)=1+1=2")
Аналитическое представление процессов удержания
Красный график отображает функцию в системе ДУ, синий график - функцию . Поднимем красный график на единицу, изобразим зеленым графиком функцию .
Теперь нормируем графики и , разделив на 2, чтобы начальной точкой была .
x=x+ones(n+1);
x=x/2;
y=y/2;
plot(t, y, label="x2(t)=1/(2t+1), x2(0)=2")
plot!(t, x, label="x1(t)=(1/(t+1)+1)/2, x1(0)=(1+1)/2=1")
d = 2;
t_ = [1:b*d;]-ones(b*d);
y_ = zeros(b*d);
x_ = zeros(b*d);
for i in 1:(b*d)
y_[i] = 1/(2*(t_[i]/d)+1);
x_[i] = (t_[i]/d+2)/(2*(t_[i]/d+1));
end
plot!(t_/d,y_, line =:dashdot, label="x2(t)=1/(2t+1)")
plot!(t_/d,x_, line =:dashdot, label="x1(t)=(t+2)/2(t+1)")
Будем использовать эти функции для моделирования процессов удержания:
,
.
На основе решенной системы ДУ и этих функций спроектируем САУ в файле retention_1.engee
Сравните их графики с рисунком:
.jpg)
Проектирование САУ
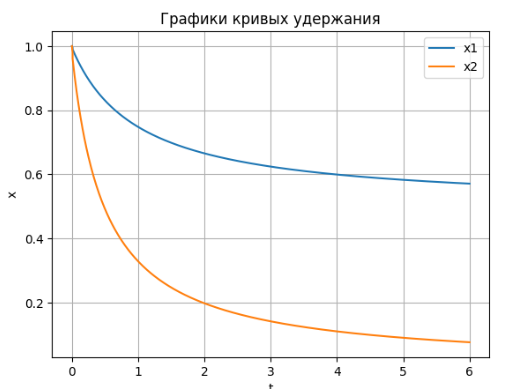
Процесс удержания
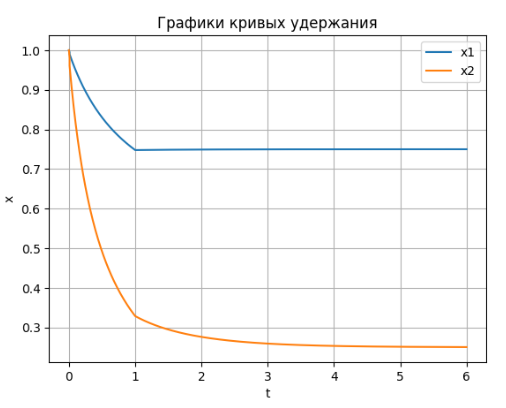
Процесс удержания
.png)
Моделирование САУ
Engee
-
Откройте файл retention_1.engee
-
Установите Final value в Ступеньке на 0.0
-
Запустите симуляцию
-
Удержание
Retention-1стабилизируется на бесконечности в значении ,Retention-2стабилизируется на бесконечности в значении
.png)
-
Измените Final value в Ступеньке на 0.25
-
Удержание
Retention-1стабилизируется в момент времени в значении
.png)
-
Измените Final value в Ступеньке на 0.444
-
Удержание
Retention-2стабилизируется в момент времени в значении
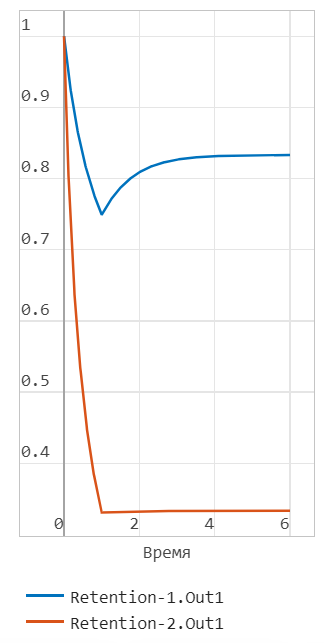
Python с помощью предложенного оператора тензорного умножения
-
Откройте файл 02_retention.ipynb
-
Задайте
u_max = 0.0 -
Запустите скрипт
-
Удержание стабилизируется на бесконечности в значении , стабилизируется на бесконечности в значении
.png)
-
Задайте
u_max = 0.25 -
Удержание стабилизируется в момент времени в значении
.png)
-
Задайте
u_max = 0.444 -
Удержание стабилизируется в момент времени в значении
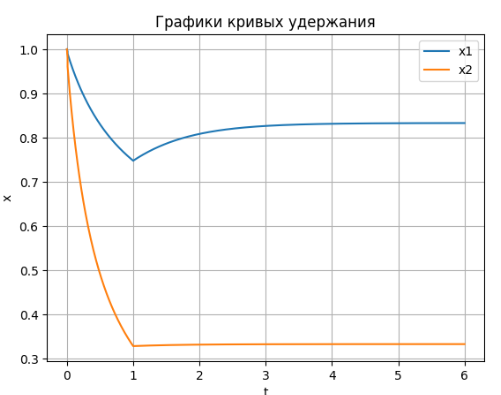
Моделирование марковских случайных процессов
Марковский процесс с непрерывным временем
См. код и графики в файле 02_retention.ipynb