SVD - разложение для сжатия изображений
Singular value decomposition (SVD) как способ сжатия изображения
Матрица - как линейный оператор
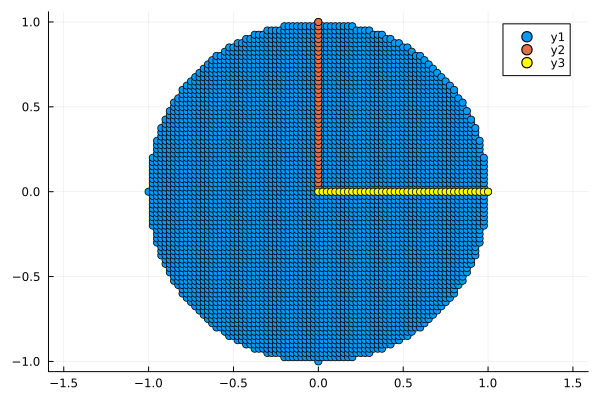
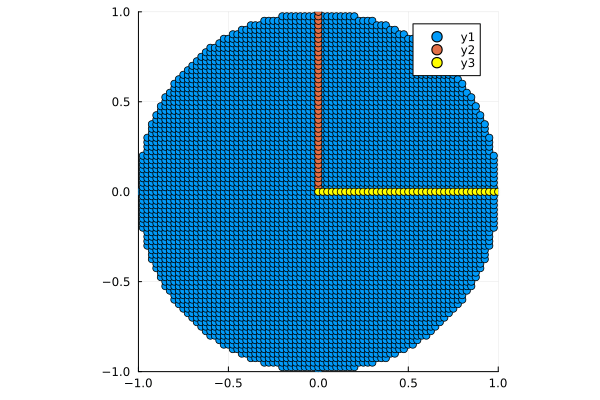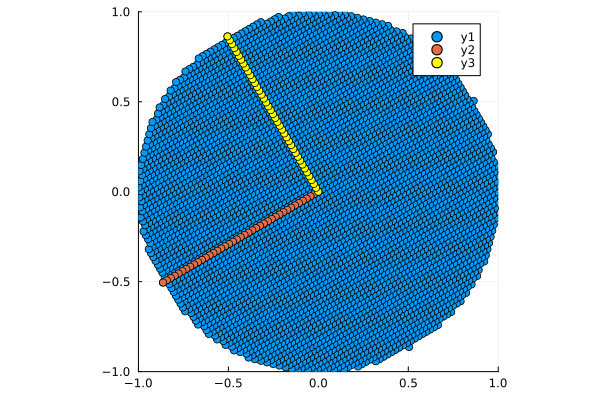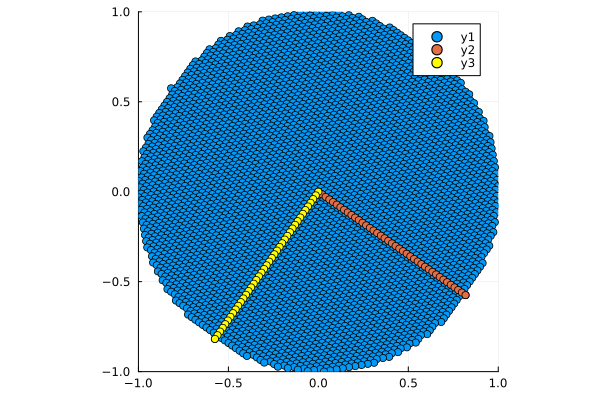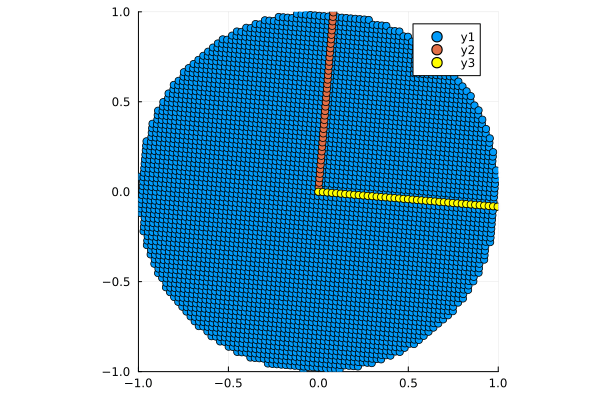
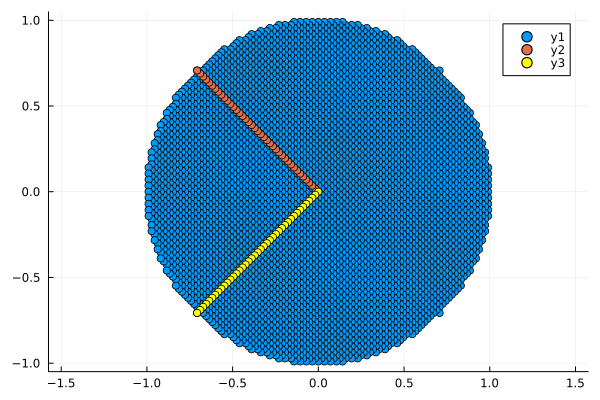
Создадим набор точек в виде круга
using LinearAlgebra
using Plots
circ_range = -1:0.025:1
# создаждим вектор векторов, содержащих координаты точек, входящих в круг
circle = [[i,j] for i = circ_range for j = circ_range if i^2 + j^2 <= 1]
# выбираем точки с координатами [x, 0] и [0,y] для отображения базиса
x_zero_indxs = findall(x-> x[1] == 0 && x[2] >= 0,circle)
y_zero_indxs = findall(x-> x[2]== 0 && x[1] >= 0,circle)
# превращаем вектор векторов в матрицу
circle = stack(circle)
function plot_circle(circle;xlm=[],ylm=[])
scatter(circle[1,:],circle[2,:],aspect_ratio=:equal)
scatter!(circle[1,x_zero_indxs],circle[2,x_zero_indxs],aspect_ratio=:equal)
if (isempty(xlm) || isempty(ylm))
scatter!(circle[1,y_zero_indxs],circle[2,y_zero_indxs], color=:yellow,aspect_ratio=:equal)
else
scatter!(circle[1,y_zero_indxs],circle[2,y_zero_indxs],
color=:yellow, xlims=xlm, ylims=ylm, aspect_ratio=:equal)
end
end
plot_circle(circle)
Обратим внимание на наши базисы. Сейчас базис x = a y -
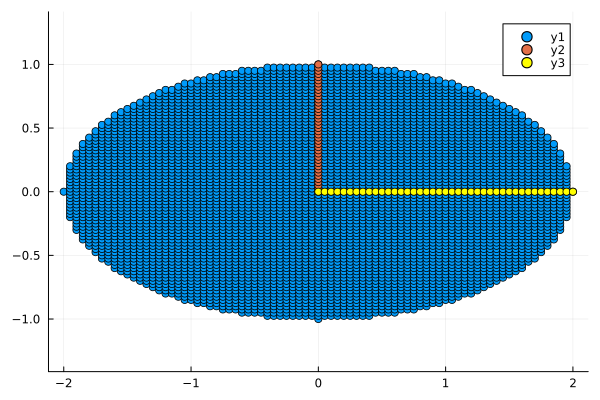
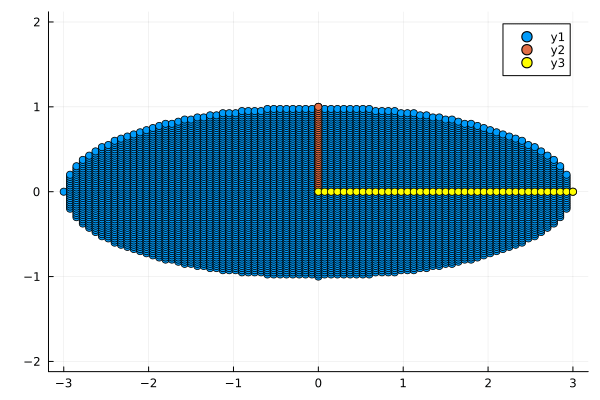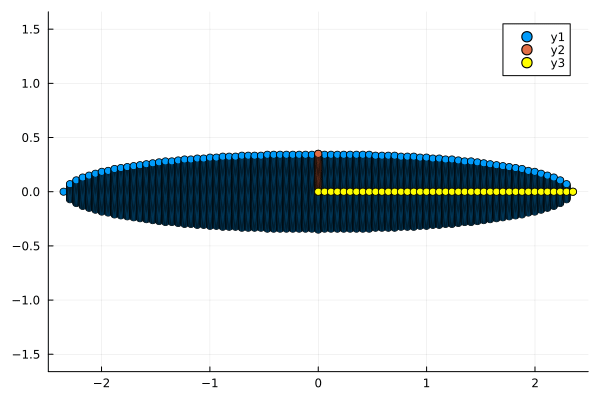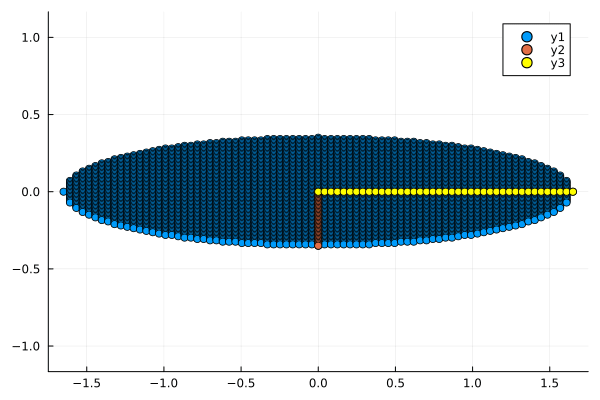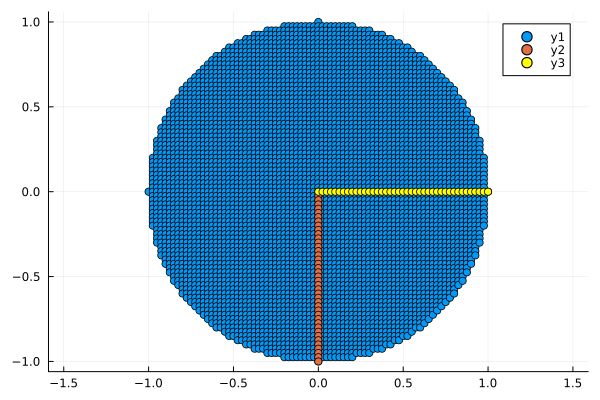
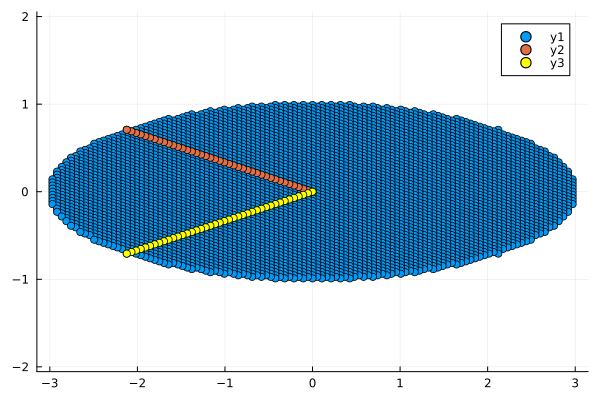
Теперь умножим наш набор точек на матрицу . \text{И} \text{теперь} \text{можем} \text{заметить}, \text{что} \text{координаты} \text{нового} \text{базиса} x \text{в} \text{предыдущих} = . И вся окружность вытянулось по горизонтали
M = [2 0;
0 1]
circle_x_2 = M * circle
plot_circle(circle_x_2)
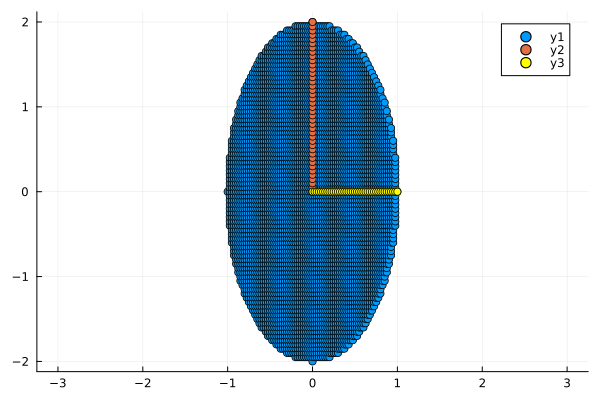
# То же для y
M = [1 0;
0 2]
circle_y_2 = M * circle
plot_circle(circle_y_2)
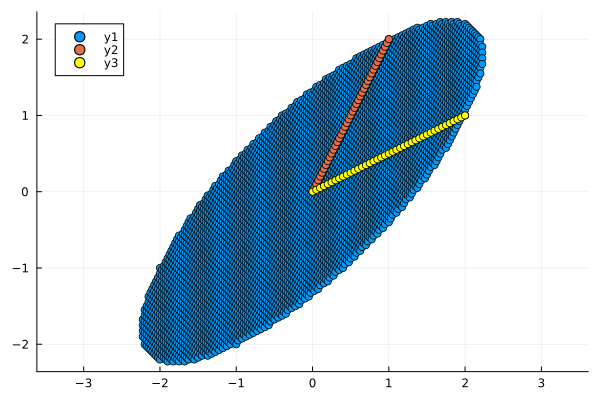
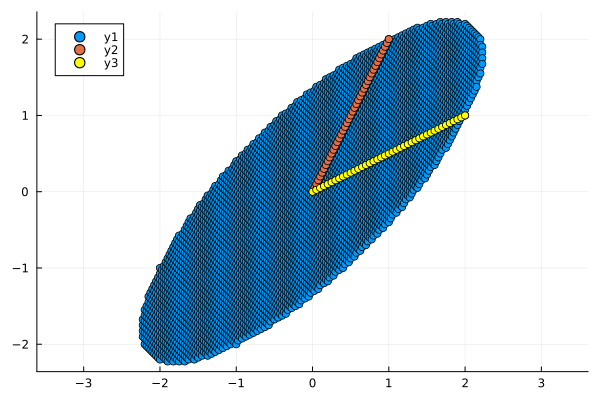
# Обратите внимание на координаты базисов и матрицу M
M = [2 1;
1 2]
circle_xy_2 = M * circle
plot_circle(circle_xy_2)
# Создадим анимации
function step!(M)
return (M * circle)
end
@gif for i=0:0.05:2
plot_circle(step!([ i 0;
0 i]),
xlm=[-2, 2],ylm=[-2, 2])
end
# Такого рода движение называется отражением
@gif for i=0:0.05:2
plot_circle(step!([ 3-i 0;
0 1-i]))
end
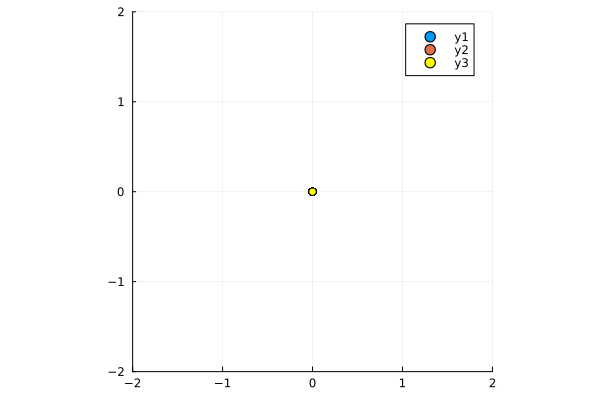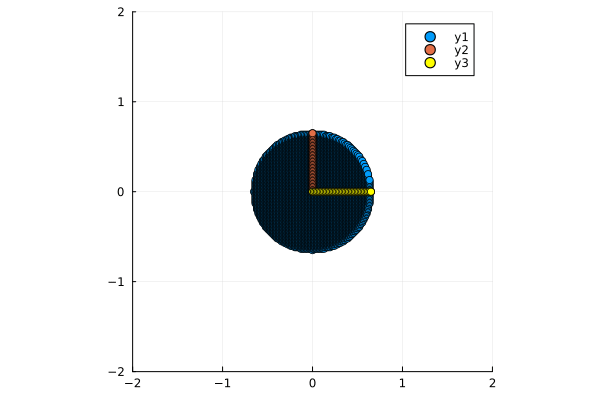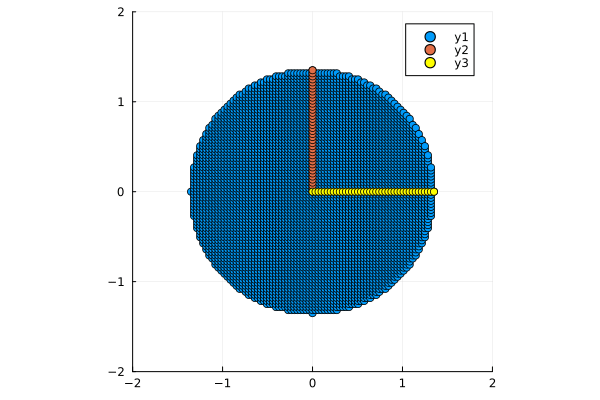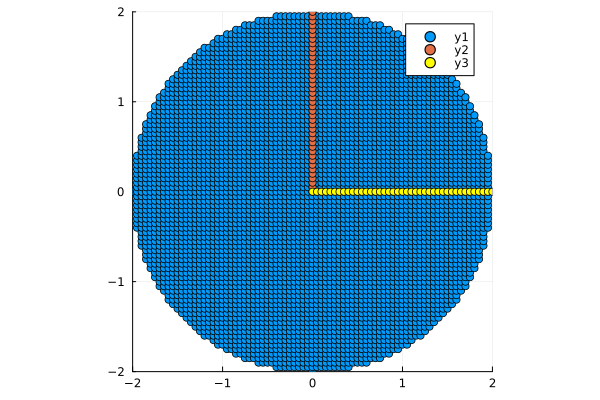
@gif for i=0:0.1:2 * π
plot_circle(step!([ cos(i) -sin(i);
sin(i) cos(i)]), xlm=[-1,1], ylm=[-1,1])
end
M = [2 1; 1 2]
(U, Σ, V) = svd(M) # разложим матрицу M
# используем foreach вместо map, так как нам не нужен вывод значений,
# а не возвращаемое значение display
foreach([U,Σ,V]) do x
display(x)
end
# Матрица V - матрица поворота или отражения
plot_circle(V * circle)
# diagm(Σ) - матрица масштабирования
plot_circle(diagm(Σ) * V * circle)
# Матрица V - матрица поворота или отражения
plot_circle(U * diagm(Σ) * V * circle)
# получили тот же результат, что и просто от матрицы M
using Images
using TestImages
Рассмотрим другой смысл использования SVD.
Изображение представляет собой прямоугольную матрицу (в нашем случае 3 прямоугольные):
img = float.(testimage("mandrill"))
channels = channelview(img) # представим нашу картину в виде цветовых каналов
# Посмотрим, как картинка раскладывается на RGB
# Заметно, что по каналу Red (левая нижняя картинка)
# нос и глаза очень красные (белый ~ max red)
chnl_views = map(channel -> colorview(Gray,
eachslice(channels;dims=1)[channel]),[1,2,3])
mosaicview(img,chnl_views...; nrow=2, npad=10)
Создадим функцию, которая будет отбирать только первые k сингулярных чисел.
Таким образом, нам нужно будет хранить не картинку, а 2 матрицы и 1 диагональ. И чтобы восстановить картину нам надо будет их просто перемножить.
$ M = U \cdot \Sigma \cdot V$
function rank_approx(F::SVD, k)
U, Σ, V = F
M = U[:, 1:k] * Diagonal(Σ[1:k]) * V[:, 1:k]'
println("size of U, Σ, V non-zero elements = $(sizeof(U[:, 1:k]) + sizeof(Σ[1:k]) + sizeof(V[:, 1:k]'))")
clamp01!(M)
end
Посмотрим, как изменилось изображение и сколько весят SVD-элементы
println("size of original image = $(sizeof(img))")
svdfactors = svd.(eachslice(channels; dims=1))
imgs = map((10, 50, 100)) do k
colorview(RGB, rank_approx.(svdfactors, k)...)
end
mosaicview(img, imgs...; nrow=2, npad=10)