Таблицы истинности
Построение таблиц истинности, булевых схем и выражений
В этом демонстрационном примере мы покажем, как создать дискретную модель для расчета выходных сигналов по таблице истинности и сравнить ее с моделью, созданной из логических элементов.
Описание модели
Создадим модель, которая преобразует набор битов на входе в сигнал на выходе, сформированный согласно следующей таблице истинности:
| A | B | C | Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Таблицу истинности можно задать множеством разных способов, например при помощи кода, помещенного внутри блока Engee Function.
Входные сигналы формируются при помощи генераторов импульсов Pulse Generator, у каждого следующего генератора период импульсов делится на 2 ("младший" имеет период 1 с, следующий 2 с, "старший" – 4 с) . По умолчанию все генераторы в нулевой момент времени начинают с верхнего уровня импульса (указанного в параметре Amplitude). Привычная форма для таблиц истинности подразумевает, что перечисление сигналов начинается с нижнего уровня. Чтобы не изменять фазу каждого генератора, мы применяем опеиацию Not к каждому входному каналу (при помощи соответствующим образом настроенного блока Logical Operator).
Шаг дискретизации модели равен 0.5. Каждый генератор за один полный период выдает оба значения импульса – верхнее и нижнее, с коэффициентом заполнения 50%. И так мы получаем следующую модель:
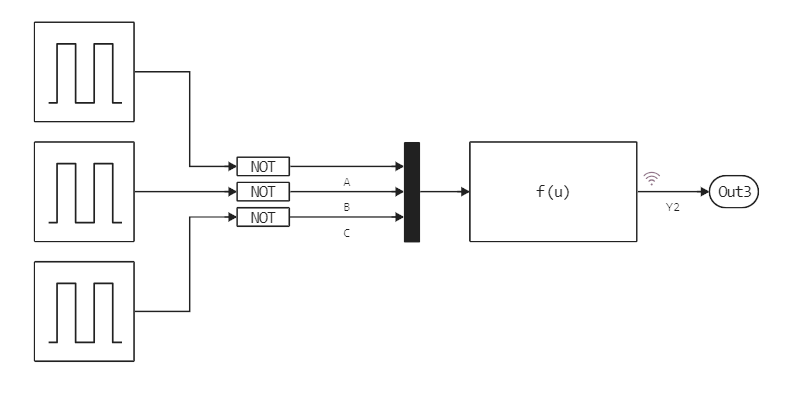
Внутри блока, таблица истинности описана следующим кодом:
function (c::Block)(t::Real, A, B, C)
if A == 0 && B == 0 && C == 0 return 0;
elseif A == 0 && B == 0 && C == 1 return 0;
elseif A == 0 && B == 1 && C == 0 return 1;
elseif A == 0 && B == 1 && C == 1 return 0;
elseif A == 1 && B == 0 && C == 0 return 1;
elseif A == 1 && B == 0 && C == 1 return 0;
elseif A == 1 && B == 1 && C == 0 return 1;
elseif A == 1 && B == 1 && C == 1 return 0;
else return 0; end;
end
Такую же схему мы можем создать при помощи логических элементов И, ИЛИ, НЕ.
Нашей таблице истинности соответствует уравнение, описанное формулой ). Его легко реализовать при помощи нескольких блоков Logical Operator.
.png)
Либо при помощи выражения (u[1] || u[2]) && !u[3] внутри блока Fcn.
.png)
Запуск модели
Запустим модель при помощи команд программного управления:
modelName = "truth_tables"
# Если модель еще не открыта, загрузим из файла
if modelName ∉ [m.name for m in engee.get_all_models()] engee.load( "$(@__DIR__)/$modelName.engee"); end;
data = engee.run( modelName )
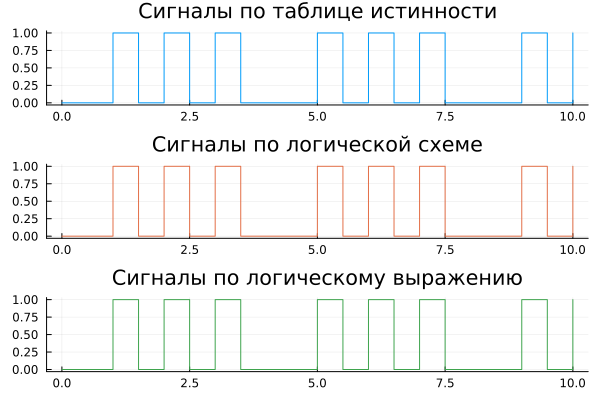
И визуализируем результат. Если преобразование таблицы истинности в логическую схему выполнено правильно, мы должны получить три идентичных графика:
gr()
plot(
plot( data["Y"].time, data["Y"].value, st=:step, lc=1, leg=false, title="Сигналы по таблице истинности" ),
plot( data["Y1"].time, data["Y1"].value, st=:step, lc=2, leg=false, title="Сигналы по логической схеме" ),
plot( data["Y1"].time, data["Y2"].value, st=:step, lc=3, leg=false, title="Сигналы по логическому выражению" ),
layout=(3,1)
)
Заключение
Мы построили несколько простых моделей, которые могут служить для изучения микроэлектроники или для создания окружения для тестирования цифровых устройств.