Телевидение с медленной развёрткой

В данном примере мы рассмотрим протокол передачи изображения на основе Slow Scan Television (SSTV) — это телевидение с медленной развёрткой, или малокадровое телевидение. Это уникальный и гибкий протокол передачи изображений, который идеально подходит для узкополосных каналов связи. Вариативность SSTV позволяет адаптировать передачу под конкретные условия, а простота реализации делает его популярным среди радиолюбителей. Однако из-за низкой скорости передачи SSTV не подходит для задач, требующих высокой скорости или высокого качества изображения.

Данная модель не привязана ни к какому стандарту связи, реализованному на практике, и описывает в первую очередь технологии и методы, которые мы можем применить в Engee для подобных систем.

Общий принцип работы SSTV заключается в передаче статических изображений через узкополосные каналы связи, таких, как радиоканалы. Процесс можно разделить на несколько этапов: кодирование изображения, модуляция, передача, приём, демодуляция и декодирование.

Далее перейдём к реализованной модели.

Анализ модели

На входе модели реализована следующая логика: мы считываем в модель изображение при помощи библиотеки Images и выполняем нормализацию изображения.

using Images

path_img = "$(@__DIR__)/img.jpg"
inp_img = imrotate(Gray.(load(path_img)), deg2rad(-90))

S = size(inp_img)
println("Размер входного изображения: $(S))")

Размер входного изображения: (160, 160))

В данном примере все работы с изображением будут проводиться в формате серых отенков представления. Если мы рассматриваем представления Julia, то это означет, что пиксели кодируются в диапозоне от 0 до 1, где 0 – чёрный цвет, а 1 – белый.

Gray.([1,0])

Теперь перейдём к следующиму блоку – блоку перемежения. Перемежение – используемая в системах передачи данных методика для повышения устойчивости к ошибкам. Основная идея заключается в том, чтобы изменить порядок данных перед передачей, и тогда соседние биты или символы окажутся разнесены в потоке.

Данный блок реализован при помощи Engee Function. На входе у него есть количество групп перемежения и сам входной сигнал.

Формула перемежения:

index = mod((i - 1) * n, N) + div(i - 1, div(N, n)) + 1

Формула деперемежения:

index = mod((i - 1), n) * div(N, n) + div(i - 1, n) + 1

Эти формулы гарантируют, что индекс не выйдет за пределы массива, так как используется операция mod для ограничения индекса в пределах N.

Сравним сами формулы.

1. Есть разница в вычислении позиции внутри группы. В первой формуле позиция внутри группы вычисляется следующим образом: mod((i−1),n). Во второй формуле позиция внутри группы вычисляется так: mod((i−1)×n,N).

2. Также имеются различия в вычислении номера группы. В первой формуле номер группы вычисляется так: div(i−1,n). Во второй формуле номер группы вычисляется таким способом: div(i−1,div(N,n)).

То есть, как мы видим, они взаимообратимы. Далее рассмотрим простой пример реализованного нами перемежения.

L = 4
data_in = collect(1:L)
n = 2 # части массива
println("Исходные данные: ", data_in)

# Функция перемежения
N = length(data_in)
interleaved_data = similar(data_in)

for i in 1:N
    index = mod((i - 1) * n, N) + div(i - 1, div(N, n)) + 1
    interleaved_data[i] = data_in[index]
end

println("Перемеженные данные: ", interleaved_data)

# Функция деперемежения
N = length(interleaved_data)
deinterleaved_data = similar(interleaved_data)

for i in 1:N
    index = mod((i - 1), n) * div(N, n) + div(i - 1, n) + 1
    deinterleaved_data[i] = interleaved_data[index]
end

println("Деперемеженные данные: ", deinterleaved_data)

Исходные данные: [1, 2, 3, 4]
Перемеженные данные: [1, 3, 2, 4]
Деперемеженные данные: [1, 2, 3, 4]

Как мы видим, алгоритм работает корректно. Теперь зададим количество групп для нашей модели.

num = 400 # Количество групп
println("Количество значений в группе: $((S[1]*S[2])/num)")

Количество значений в группе: 64.0

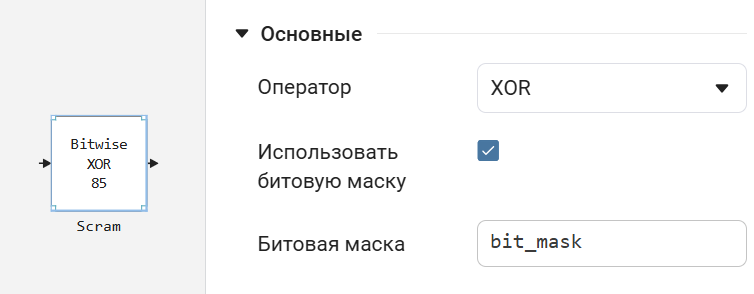
Следующий блок, который мы используем, – это XOR. Данная операция обратимая и позволяет реализовать простой вариант скремблера.

Скремблер (от англ. scramble — шифровать, перемешивать) — программное или аппаратное устройство, выполняющее скремблирование, то есть обратимое преобразование цифрового потока без изменения скорости передачи с целью получения свойств случайной последовательности. После скремблирования появление «1» и «0» в выходной последовательности равновероятны.

Далее зададим битовую маску для нашего скремблера.

bit_mask = 0b01010101 # max 8 bit
println("bit_mask: $bit_mask")

bit_mask: 85

Следующие блоки, которые мы рассмотрим, — это связка 16-FSK-модуляции и автоматической регулировки усиления (АРУ).

FSK — это метод модуляции, при котором цифровые данные (биты) передаются путём изменения частоты несущего сигнала. Каждому значению бита (0 или 1) или группе битов соответствует определённая частота. 16-FSK — это расширение FSK, где используется 16 различных частот для передачи 4 бит данных одновременно. Таблица соответствия бит и чисел для 16-FSK:

Комбинация бит	Число
[0, 0, 0, 0]	1
[0, 0, 0, 1]	3
[0, 0, 1, 0]	5
[0, 0, 1, 1]	7
[0, 1, 0, 0]	9
[0, 1, 0, 1]	11
[0, 1, 1, 0]	13
[0, 1, 1, 1]	15
[1, 0, 0, 0]	-1
[1, 0, 0, 1]	-3
[1, 0, 1, 0]	-5
[1, 0, 1, 1]	-7
[1, 1, 0, 0]	-9
[1, 1, 0, 1]	-11
[1, 1, 1, 0]	-13
[1, 1, 1, 1]	-15

АРУ — это система, которая автоматически регулирует уровень усиления сигнала на приёмной стороне, чтобы поддерживать постоянный уровень выходного сигнала независимо от изменений уровня входного сигнала. В нашем случае реализована логика, которая рассчитывает мощность выхода относительно данных до усиления сигнала, но вы легко можете заменить этот подход на заданное значение.

Исходя из теста, приведённого ниже, мы явно можем сделать вывод, что при 16-FSK мощность желаемого сигнала равна 85 Вт.

norm_img = ((channelview(inp_img))[:])
power_img = sum(norm_img.^2) / length(norm_img)
println("Мощность входного сигнала: ", power_img, " Вт")

values = [1:2:15; -1:-2:-15] 
v = [values[rand(1:length(values))] for _ in 1:length(norm_img)]
power_desired = sum(v .^ 2) / length(v)
println("Желаемая мощность: ", power_desired, " Вт")

K = sqrt(power_desired / power_img) # Используем квадратный корень, так как мощность пропорциональна квадрату амплитуды 
println("Коэффициент усиления: ", K)

amplified = norm_img .* K  # Усиленный сигнал

power_out = sum(amplified .^ 2) / length(amplified) 
println("Мощность выходного сигнала: ", round(power_out, digits=2), " Вт")

Мощность входного сигнала: 0.3573653492647059 Вт
Желаемая мощность: 84.9459375 Вт
Коэффициент усиления: 15.417540102273989
Мощность выходного сигнала: 84.97 Вт

Следующие блоки, которые мы рассмотрим, — FM Modulator Baseband и FM Demodulator Baseband. Это модуляция, которая преобразует базовый сигнал в частотно-модулированный (FM) сигнал.

В FM-радиовещании используются два ключевых параметра.

1. Несущая частота – это основная частота сигнала, которая модулируется для передачи информации. В диапазоне FM-вещания она находится между 87,5 МГц и 108 МГц.

2. Частота девиации – это максимальное отклонение частоты от несущей частоты при передаче сигнала. Для стандартного FM-вещания максимальная допустимая девиация составляет ±75 кГц.

Таким образом, если несущая частота равна, скажем, 100 МГц, то реальная частота передаваемого сигнала будет колебаться в пределах от 99,925 до 100,075 МГц.

fs = 100e3 # Hz
println("Несущая частота: $fs Гц")

deviation_fs = fs * 0.05 # 5% от fs
println("Частота девиации: $deviation_fs Гц")

Несущая частота: 100000.0 Гц
Частота девиации: 5000.0 Гц

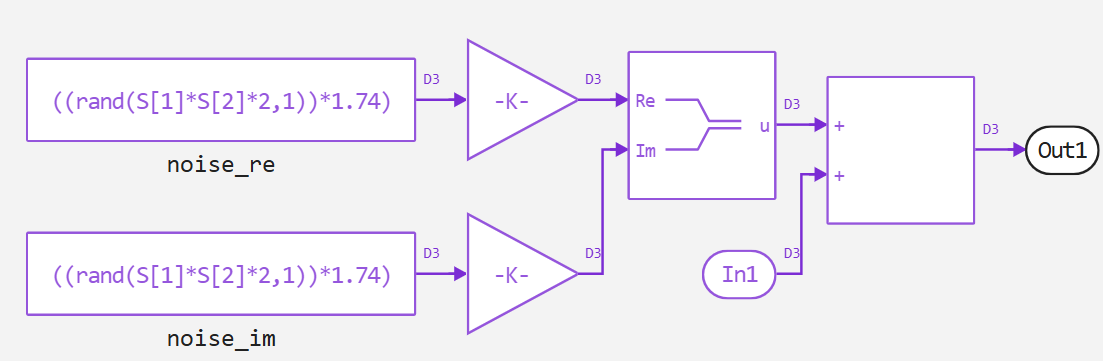
Последний блок, который мы рассмотрим, — это блок канала связи. Для наложения шума он использует метрику Signal-to-Noise Ratio (SNR), отношение сигнал/шум. Данная метрика показывает, насколько полезный сигнал сильнее шума.

Чем выше SNR, тем выше качество сигнала, так как шум меньше влияет на данные. И, наоборот, чем ниже SNR, тем ниже качество сигнала, потому что шум начинает доминировать над полезным сигналом.

Например:

1. если SNR = 20 дБ, это означает, что сигнал в 100 раз мощнее шума (в линейной шкале);
2. если SNR = 0 дБ, это означает, что мощность сигнала и шума равны;
3. если SNR = -10 дБ, это означает, что шум в 10 раз сильнее сигнала.

snr = 10;
println("SNR: $snr дБ")
snr_linear = 10^(snr / 10)
signal_power = 1
noise_power = 1 / snr_linear
println("Мощность шума: $noise_power")

SNR: 10 дБ
Мощность шума: 0.1

Запуск модели и анализ результатов

Зададим параметры симуляции и запустим модель.

st = 1/fs*S[1]*S[2] # Sample time
println("Время одного отсчёта: $st")
step = st/S[1]/S[2]
println("Шаг решателя: $step")
time_stop = st*2.1
println("Шаг моделирования: $st")

Время одного отсчёта: 0.256
Шаг решателя: 1.0e-5
Шаг моделирования: 0.256

name_model = "SSTV"
Path = (@__DIR__) * "/" * name_model * ".engee"

if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
    model = engee.open( name_model ) # Открыть модель
    model_output = engee.run( model, verbose=true ); # Запустить модель
else
    model = engee.load( Path, force=true ) # Загрузить модель
    model_output = engee.run( model, verbose=true ); # Запустить модель
    engee.close( name_model, force=true ); # Закрыть модель
end
sleep(1)

Building...
Progress 0%
Progress 5%
Progress 11%
Progress 16%
Progress 22%
Progress 28%
Progress 34%
Progress 39%
Progress 45%
Progress 50%
Progress 60%
Progress 67%
Progress 72%
Progress 81%
Progress 87%
Progress 93%
Progress 99%
Progress 100%
Progress 100%

Визуализируем результаты работы нашей модели и подведём итоги.

println("SNR: $snr дБ")
println()
ber = ((collect(BER)).value)[end] 
println("Всего бит: $(Int(ber[3]))")
println("Кол-во ошибок: $(Int(ber[2]))")
println("BER: $(round(ber[1], digits=2))")

inp = plot(framestyle=:none, grid=false, title = "Вход")
heatmap!( 1:S[2], 1:S[1], permutedims(inp_img, (2, 1)), colorbar=false)

sim_img = imrotate(colorview(Gray, ((collect(img_FM))[3,:].value)), deg2rad(-90))
sim = plot(framestyle=:none, grid=false, title = "Выход")
heatmap!( 1:size(sim_img, 2), 1:size(sim_img, 1), permutedims(sim_img, (2, 1)), colorbar=false)

sim_error = (collect(error_sim)).value 
Average_error = round(sum(abs.(sim_error))/length(sim_error)*100, digits=2)
err = plot(sim_error, title = "Cредняя ошибка равна $Average_error % ")

plot(plot(inp, sim), err, layout = grid(2, 1, heights=[0.7, 0.3]), legend=false) 

SNR: 10 дБ

Всего бит: 430088
Кол-во ошибок: 39938
BER: 0.09

Как видно из результатов моделирования, на выходе мы получаем хорошие показатели BER. Если мы более детально займёмся настройкой перемежения и скремблирования, то сможем получить ещё более достойное качество картинки. Для этих целей вам предоставляется второй скрипт SSTV_test. В нём нет лишнего описания, а приведён только код данного проекта.

Вывод

В данном примере мы рассмотрели возможности моделирования в Engee протокола передачи изображения на основе телевидения с медленной развёрткой, а также изучили множество инструментов, позволяющих выполнять такие проекты в Engee. Как видно из нашего примера, в Engee, есть все необходимые функции и инструменты для этих моделей, и они работают корректно.