"Точное" восстановление сигнала
Введение
Одной из моих рабочих задач в прошлом было написать низкоуровневым программистам алгоритм действий при передискретизации цифрового потока с частотой дискретизации 4000 Гц (80 точек на период) в 2400 Гц (48 точек на период). Дело в том, что сторонним устройством выдавался поток (токи и напряжения энергосистемы) 80 точек (по стандарту МЭК61850 9.2 LE), а ЦОС нашего устройства был написан исходя из частоты 2400 Гц. Чтобы не переделывать ЦОС в нашем устройстве, было решено преобразовывать "на лету" входные точки. Устройство работает циклически, и каждые 20 точек на входе преобразовывались в 12 точек перед поступлением в "математику".
Это стандартная задача передискретизации (resampling) сигнала. Соотношение между частотами равно , то есть нужно повысить частоту в три раза (upsampling), а потом снизить в 5 раз (downsampling). Задача была решена общепринятым способом, с использованием полифазной структуры (сигнал, с вставленными двумя нулями между каждыми отсчетами, порциями по 5 штук подавался на ФНЧ). Низкочастотные фильтры были выбраны с линейной ФЧХ, так как мы не хотели менять фазовые соотношения между гармониками сигнала. Фильтры неидеальны и вносят свою погрешность, но конечный результат устроил нас и по точности и по скорости (времени реакции на "ступеньку").
Рассуждения на тему
По мере выполнения данной работы возникали и обсуждались следующие моменты:
-
Источник данных (ПАС - преобразователь аналогового сигнала) - это трансформатор + АЦП + генератор Ethernet потока. Перед АЦП стоят антиалиасинговые фильтры. Сигналы энергосистемы в основном - это узкополосные сигналы и частота дискретизации 4000 Гц достаточна для фиксации всех информационно важных составляющих сигнала. Итого, в 80-ти точках за период есть вся информация о сигнале.
-
У нас есть информация о сигнале, представленная в виде дискретных отсчетов. У нас есть теорема Котельникова, которая говорит, что сигнал можно восстановить точно. Если мы можем это сделать, то далее мы можем взять с восстановленного аналогового сигнала новые точки с нужной нам частотой дискретизации.
-
Если мы можем сделать передискретизацию точно, зачем мы используем стандартный (заведомо неточный) способ через upsampling, фильтрацию и downsampling?
Далее мы обсудим все эти моменты.
Что там с точным восстановлением?
Действительно, в 1933 году была доказана теорема отсчетов (теорема Котельникова), которая утверждает возможность точного восстановления сигнала, состоящего из частот от до по его дискретным отсчетам, взятым с частотой не менее . Восстановление производится с помощью ряда Котельникова:
где - номер точки;
- период дискретизации, с.
Прошу обратить внимание на бесконечные пределы суммирования. Давайте сразу попробуем восстановить близкий энергетикам сигнал - синусоиду и не тратить время на прямоугольные импульсы.
gr();
T0 = 0.02
T = T0 / 2.7
N = 20
t = range(start = -N * T0, stop = N * T0, step = T)
omega = 100*pi
y = sin.(omega*t)
time_ = range(start=-N*T0, stop=N*T0, step=1e-4)
yAnalog = sin.(omega*time_)
anim = let
analogSignal = zeros(length(time_))
z = Int(round(length(t)/2))
@animate for i in eachindex(t)
analogSignal += y[z] * sinc.((time_ .- t[z]) / T)
p = plot(t, y,
seriestype =:scatter,
title = "Восстановление синуса по дискретным точкам. fs = 2.7f0",
xlims = (-N*T0, N*T0),
ylims = (-1.1, 1.1),
legend = false,
size = (1200, 250),
xlabel = "Время, с")
vspan!([-0.01, 0.01],
alpha = 0.2,
color = :green)
plot!(p,
time_, analogSignal,
linewidth = 2,
color=:blue)
scatter!([t[z]], [y[z]],
color=:red,
markersize = 6,
markershape = :pentagon)
z += (-1)^i * i
if z == 0 || z > length(t)
break
end
end
end
gif(anim, "precRec/nonperiod.gif", fps=10)
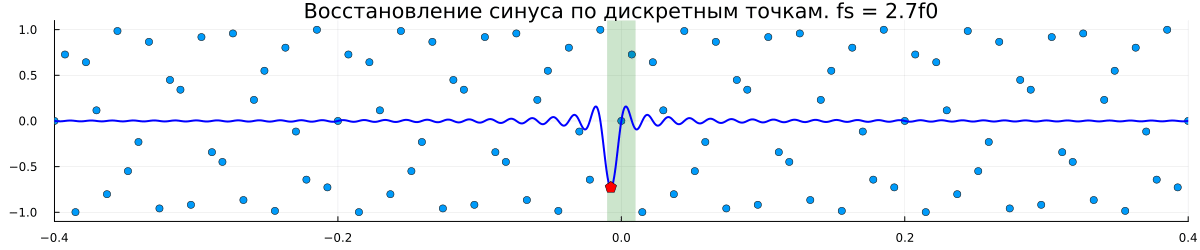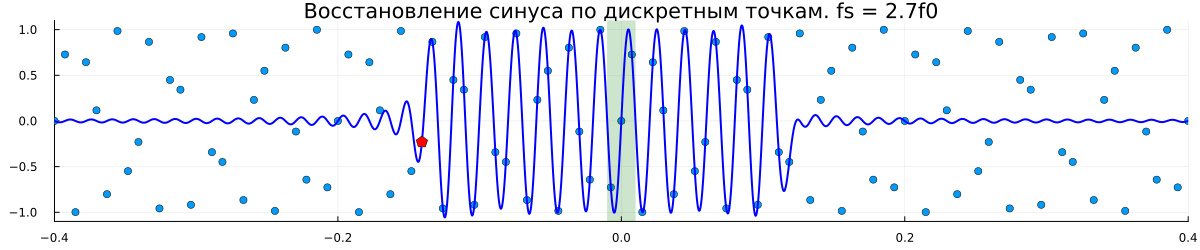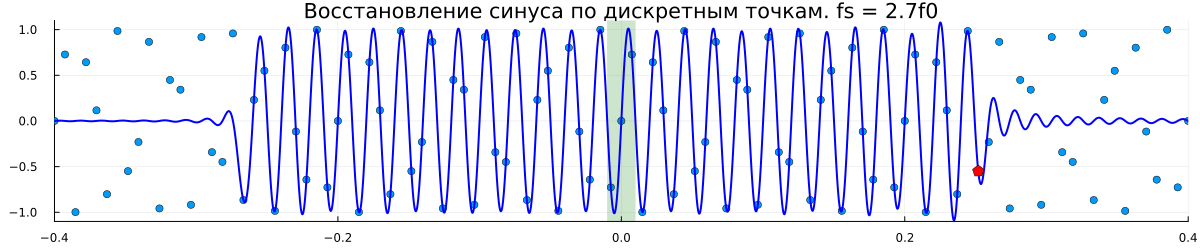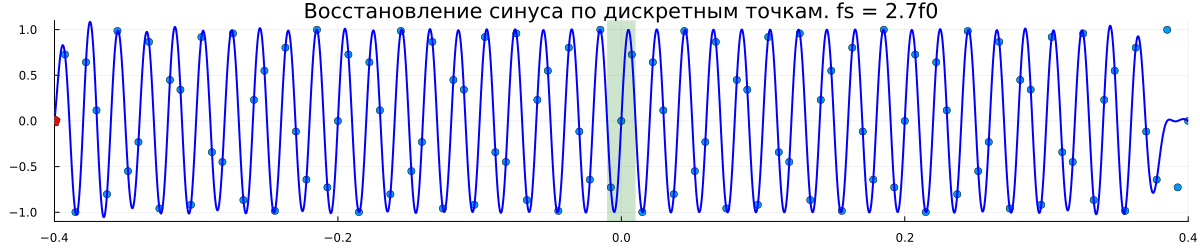
Комментарии к графику
-
Частота дискретизации специально выбрана некратной частоте сигнала, чтобы показать, что восстановление возможно даже по таким, на первый взгляд, хаотично разбросанным точкам;
-
В центре графика выделен зеленой областью один период синусоиды. По мере увеличения количества точек, участвующих в восстановлении сигнала, этот центральный фрагмент всё ближе и ближе к истинному синусу. К сожалению, для точного восстановления необходимо продолжать суммирование до бесконечности в обе стороны.
-
Более равномерная (по периоду) дискретизация качественно процесс и результат не изменит.
Вывод
Теорему Котельникова для точного восстановления на практике использовать затруднительно, так как требуется привлечение (в теории) всех точек сигнала. Функция непериодическая и не очень подходит для восстановления периодических сигналов.
Точное восстановление периодических сигналов
Еще один способ восстановления аналогового сигнала по дискретным отсчетам дает пара (прямое и обратное) дискретных преобразований Фурье.
Формула для восстановления аналогична ряду Котельникова и выглядит как (при нечетном ):
где - количество дискретных отсчетов сигнала;
- номер точки;
- период дискретизации, с.
Так же как и в ряде Котельникова мы имеем набор "взвешенных" и смещенных функций интерполянтов. Существенное отличие в том, что теперь диапазон суммирования конечен и интерполянт это периодическая функция. Сама функция это одно из определений ядра Дирихле.
Попробуем применить! В коде будем использовать функцию diric пакета DSP.jl.
using DSP
T0 = 0.02
NN = 12
T = T0 / NN
N = 3
t = range(start=-T0/2, stop=T0/2-T, step=T)
omega = 100*pi
y = sin.(omega*t)
time_ = range(start=-N*T0, stop=N*T0, step=1e-4)
yAnalog = sin.(omega*time_)
anim = let
@animate for i in eachindex(t)
analogSignal = zeros(length(time_))
for j = 1:i
if iseven(i)
analogSignal += y[j] * diric.((time_ .- t[j]) / T * 2pi / i, i) .* cos.((time_ .- t[j]) / T / i * pi)
else
analogSignal += y[j] * diric.((time_ .- t[j]) / T * 2pi / i, i)
end
end
q = plot(t, y,
seriestype =:scatter,
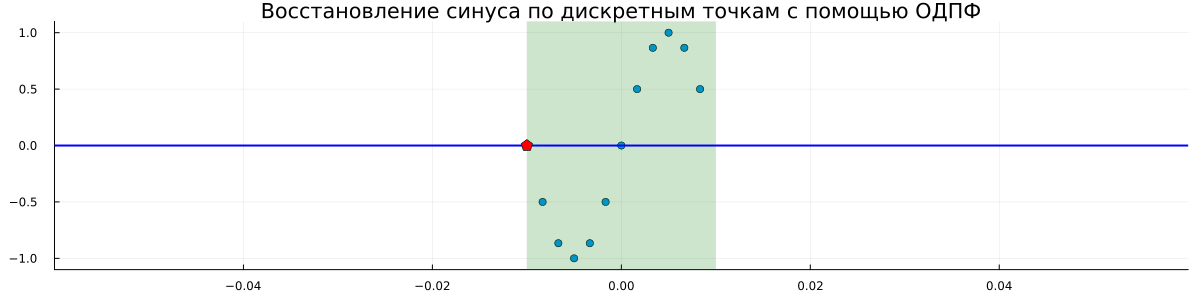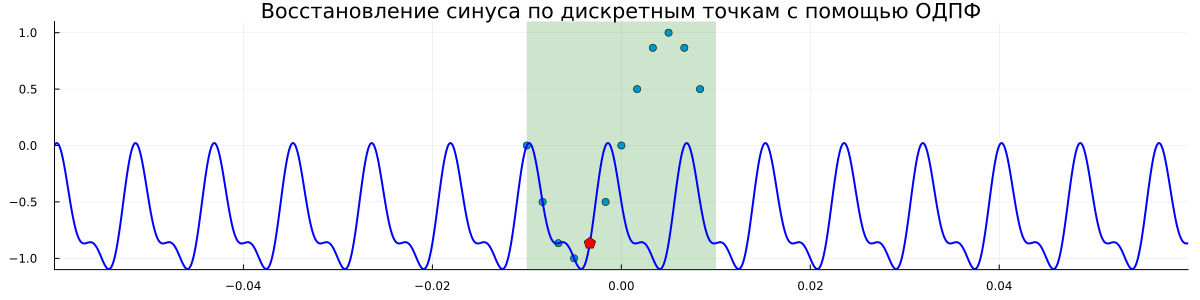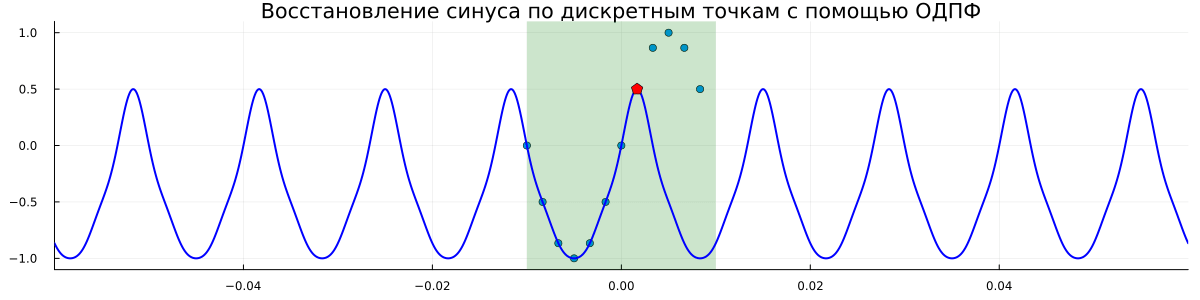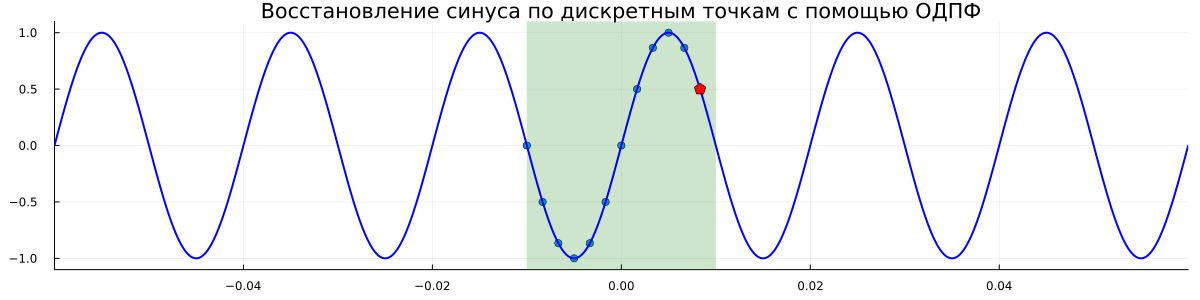
title = "Восстановление синуса по дискретным точкам с помощью ОДПФ",
xlims = (-N*T0, N*T0),
ylims = (-1.1, 1.1),
legend = false,
size = (1200, 300),
xlabel = "Время, с")
vspan!([-0.01, 0.01],
alpha = 0.2,
color = :green)
plot!(q,
time_, analogSignal,
linewidth = 2,
color=:blue)
scatter!([t[i]], [y[i]],
color=:red,
markersize = 6,
markershape = :pentagon)
end
end
gif(anim, "precRec/period.gif", fps = 1)
Комментарии к графику
- Видно, что восстановленные функции всегда периодичны. Период увеличивается по мере привлечения всё новых точек. То есть независимо от реального периода аналоговой синусоиды мы всегда восстанавливаем периодический сигнал по тем точкам, которые доступны;
- Как только мы используем все точек аналоговая функция синуса восстанавливается точно.
Вывод
Ядро Дирихле гораздо лучше подходит для восстановления периодических сигналов (точнее результат восстановления всегда будет периодической функцией). Если входные дискретные точки также "взяты" ровно с периода аналогового сигнала, то получится точное восстановление.
Практика
На практике выше изложенные методы не пользуются популярностью.
Интерполяция с помощью ряда Котельникова требует, во-первых, привлечения большого количества точек, во-вторых, спектр сигнала должен быть ограничен. Но кто знает насколько хорошо был ограничен спектр перед дискретизацией, чтобы утверждать, что мы действительно восстанавливаем изначальный аналоговый сигнал.
Интерполяция периодических сигналов с помощью ядра Дирихле требует точки всего периода плюс мы должны быть уверены в том, что дискретные отсчеты распределены ровно по периоду. Но в приложении к энергетике частота сигнала может измениться и 80 точек, которые ранее совпадали с периодом аналогового сигнала, теперь не совпадают. Интерполяционная формула об этом ничего не знает.
С другой стороны линейная, кубическая интерполяция (или, что тоже самое - интерполяция с помощью вставки нулей и ФНЧ) не предъявляет никаких требований к сигналу и его дискретизации. Через 2 точки всегда можно провести линию, а через 4 кубический полином. Затраты на вычисление такой интерполяции (передискретизации) сильно ниже со сравнимым качеством. Поэтому такие методы и являются базой для решения задач передискретизации.