Engee Community
/
Примеры и проекты
/
Управление двигателем постоянного тока

Управление двигателем постоянного тока

Автор
avatar-daryadarya
Notebook

Управление двигателем постоянного тока

В этом примере показано сравнение трех методов управления двигателем постоянного тока:

  • прямое управление
  • управление с обратной связью
  • регулирование LQR.

Сравним эти методы с точки зрения чувствительности к возмущениям от нагрузки.

Постановка задачи

В ДПТ с якорным управлением входное напряжение $V_a$ управляет угловой скоростью вала двигателя.

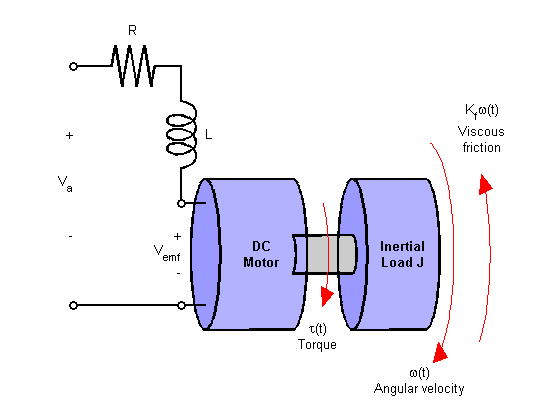
xxdcdemofigures_01.png

В этом примере показаны два способа управления ДПТ, позволяющие снизить чувствительность $\omega$ к изменениям нагрузки (изменениям крутящего момента, создаваемого нагрузкой двигателя).

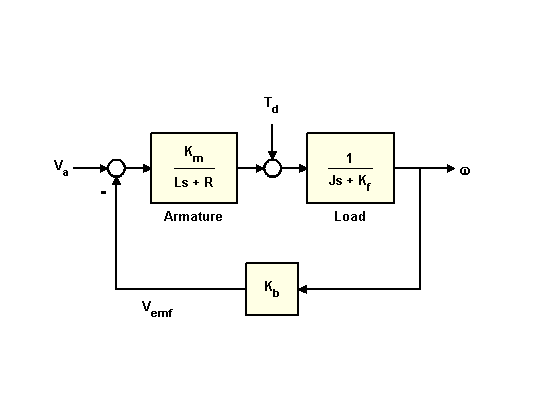
xxdcdemofigures_02.png

Упрощенная модель двигателя постоянного тока показана выше. Параметр крутящего момента $T_d$ моделирует возмущения нагрузки. Необходимо свести к минимуму колебания скорости, вызванные такими возмущениями.

Зададим параметры двигателя. В этом примере физическими константами являются:

In [ ]: 
Pkg.add(["LinearAlgebra", "RobustAndOptimalControl", "ControlSystems", "ControlSystemsBase"])
In [ ]: 
import Pkg; 
Pkg.add("ControlSystemsBase")
Pkg.add("RobustAndOptimalControl")
Pkg.add("LinearAlgebra")

   Resolving package versions...
  No Changes to `~/.project/Project.toml`
  No Changes to `~/.project/Manifest.toml`
   Resolving package versions...
  No Changes to `~/.project/Project.toml`
  No Changes to `~/.project/Manifest.toml`
   Resolving package versions...
    Updating `~/.project/Project.toml`
  [37e2e46d] + LinearAlgebra
  No Changes to `~/.project/Manifest.toml`
In [ ]: 
using ControlSystems, ControlSystemsBase, RobustAndOptimalControl, LinearAlgebra

R = 2.0 ;   
L = 0.5;     
Km = 0.1;   
Kb = 0.1;    
Kf = 0.2;    
J = 0.02;

Построим модель ДПТ с двумя входами ($V_a$,$T_d$) и одним выходом ($w$). Для начала зададим описание блоков структурной схемы, представленной выше, в виде передаточных функций.

In [ ]: 
h1 = tf([Km], [L, R])
h2 = tf([1], [J, Kf])
Out[0]:
TransferFunction{Continuous, ControlSystemsBase.SisoRational{Float64}}
    1.0
-----------
0.02s + 0.2

Continuous-time transfer function model

Установим свзязи между блоками. Назначим названия входных и выходных сигналов, определим суммирующие блоки и установим связь между блоками с помощью функции connect().

Задаем названия входным и выходным сигналам.

In [ ]: 
H1 = named_ss(h1, x = :xH1, u = :uH1, y = :yH1)
H2 = named_ss(h2, x = :xH2, u = :uH2, y = :yH2)
Kb = named_ss(ss(Kb), x = :xKb, u = :uKb, y = :yKb)

Указываем сигналы, которые поступают и выходят из суммирующих блоков.

In [ ]: 
Sum1 = sumblock("uH1 = Va - yKb")
Sum2 = sumblock("uH2 = yH1 + Td")

Устанавливаем соответствия между выходами и входами блоков.

In [ ]: 
connections = [
    :uH1 => :uH1;
    :yH1 => :yH1;
    :uH2 => :uH2;
    :yH2 => :uKb;
    :yKb => :yKb;   
]

Задаем внешние входные сигналы и выходной сигнал.

In [ ]: 
w1 = [:Va, :Td]
z1 = [:yH2]

Передаем параметры в функцию connect() для получения модели систем.

In [ ]: 
dcm = connect([H2, H1, Kb, Sum1, Sum2], connections; z1, w1, verbose = true)

Теперь посмотрим реакцию на единичное ступенчатое воздействие.

In [ ]: 
V_a = dcm[1,1];
plot(stepinfo(step(V_a,2.5)))
Out[0]:

При подаче на вход единичного ступенчатого воздействия ($Td=0$) установившееся значение выходного сигнала равно 0.244.

Прямое управление двигателем постоянного тока

Первый вариант управления - прямое управление. На вход системе подадим желаемое значение угловой скорости ($w_{ref}$), а также смоделируем воздействие внешнего момента ($Td$) на систему.

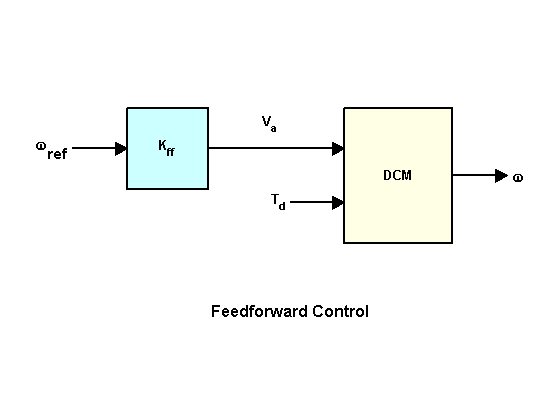
xxdcdemofigures_03.png

Коэффициент усиления прямой связи $K_{ff}$ должен быть установлен на величину обратную коэффициенту усиления по постоянному току от $Va$ до $w$.

In [ ]: 
Kff = 1/dcgain(V_a)[1]
Out[0]:
4.099999999999999

Чтобы оценить эффективность конструкции с прямой связью в условиях возмущений нагрузки, смоделируйте реакцию на пошаговую команду $w_{ref}=1$ с возмущением $Td = -0,1 Нм$ между $t=5 и t=10$ секундами:

In [ ]: 
t = 0:0.01:15
Td = -0.1 * (5 .< t .< 10)          
u = hcat( ones( length(t) ), Td )       

cl_ff = dcm * Diagonal( [Kff, 1] )   

h_1 = lsim( cl_ff, u, t )
plot( h_1, label = "Прямое управление, h_1(t)" )
plot!( t, Td, label = "Внешний возмущающий момент, Td" )
Out[0]:

Система с обратной связью

Рассмотрим второй вариант управления и опишем структуру управления с обратной связью.

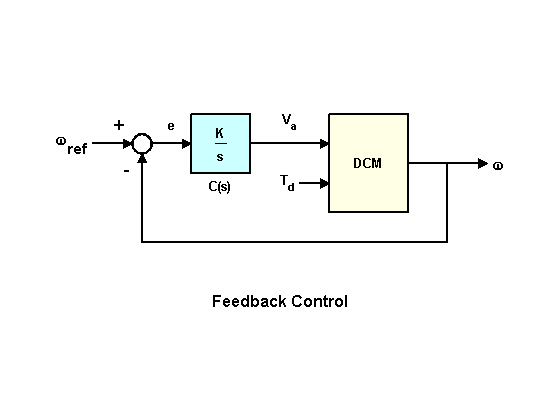
xxdcdemofigures_04.png

Чтобы обеспечить нулевую установившуюся ошибку, используем контроллер $C(s)$ в виде интегратора с коэффициентом усиления.

Чтобы определить коэффициент усиления K, можно использовать метод корневого годографа, применяемый к передаче с разомкнутым контуром ($1/s * (Va \to w)$):

In [ ]: 
rlocusplot( ss( tf( 1, [1, 0] ) ) * V_a )
Out[0]:

Наведите на кривые, чтобы ознакомиться со значениями коэффициента усиления и соответствующего полюса. Можно заметить, что траектории двух корней пересекают мнимую ось. В этих точках $K\approx55$. Чтобы наша система оставалась устойчивой, необходимо выбрать $K<55$. Выберем $K = 5$.

In [ ]: 
K = 5;

Задаем названия входным и выходным сигналам.

In [ ]: 
C = named_ss( tf( K,[1, 0] ), x=:xC, u=:e, y=:Va )
Out[0]:
NamedStateSpace{Continuous, Float64}
A = 
 0.0
B = 
 2.0
C = 
 2.5
D = 
 0.0

Continuous-time state-space model
With state  names: xC
     input  names: e
     output names: Va

Указываем сигналы, которые поступают и выходят из суммирующих блоков.

In [ ]: 
sum = sumblock( "e = w_ref - yH2" )
Out[0]:
sumblock: NamedStateSpace{Continuous, Float64}
D = 
 1.0  -1.0

Continuous-time state-space model
With state  names: 
     input  names: w_ref yH2
     output names: e

Устанавливаем соответствия между выходами и входами блоков.

In [ ]: 
connections1 = [
    :e => :e;
    :Va => :Va;
    :yH2 => :yH2
]
Out[0]:
3-element Vector{Pair{Symbol, Symbol}}:
   :e => :e
  :Va => :Va
 :yH2 => :yH2

Задаем внешние входные сигналы и выходной сигнал

In [ ]: 
w1 = [ :w_ref, :Td ]
z1 = [ :yH2 ]
Out[0]:
1-element Vector{Symbol}:
 :yH2

Передаем параметры в функцию connect() для получения модели системы.

In [ ]: 
cl_rloc = connect( [sum, C, dcm], connections1; w1, z1 )
Out[0]:
NamedStateSpace{Continuous, Float64}
A = 
 0.0   -12.5      0.0
 0.0   -10.0      3.2
 1.25   -0.3125  -4.0
B = 
 2.0  0.0
 0.0  8.0
 0.0  0.0
C = 
 0.0  6.25  0.0
D = 
 0.0  0.0

Continuous-time state-space model
With state  names: xC##feedback#237 xH2##feedback#227##feedback#237 xH1##feedback#227##feedback#237
     input  names: w_ref Td
     output names: yH2

Построим графики выходных сигналов при прямом управлении и управлении с обратной связью.

In [ ]: 
h_2 = lsim( cl_rloc, u, t )       
plot( h_1, label = "Прямое управление, h_1(t)" )
plot!( h_2, label = "Управление с обратной связью, h_2(t)" )
plot!( t, Td, label = "Внешний возмущающий момент, Td" )
Out[0]:

Результат управления с обратной связью значительно лучше прямого метода управления. Однако присутствуют пики вначале и вконце действия $Td$.

Управление двигателем постоянного тока с помощью ленейно-квадратичного регулятора

Чтобы еще больше повысить производительность, попробуем спроектировать линейно-квадратичный регулятор (LQR) для структуры обратной связи, показанной ниже.

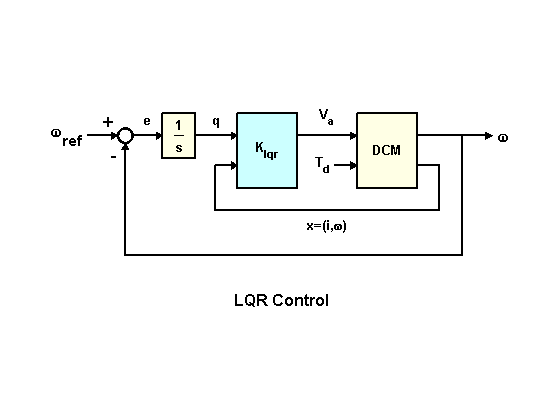
xxdcdemofigures_05.png

В дополнение к интегралу, схема LQR также использует вектор состояния $x=(i,w)$ для синтеза управляющего напряжения $Va$. Результирующее напряжение имеет вид $$ Va = K1w+K2\frac{w}{s}+K3i $$ где $i$ - ток якоря

Для лучшего подавления возмущений используем функцию стоимости, которая "наказывает" за большую интегральную ошибку. Например,

$$ C = \int_0^\infty (20q(t)^2+\omega(t)^2+0.01V_a(t)^2)\,\mathrm{d}x $$

где

$$ q(s)=\frac{\omega(s)}{s} $$

Вычислим оптимальное усиление LQR для этой функции стоимости.

Добавим выход w/s к модели dcm.

In [ ]: 
dc_aug = [ 1 ; ss( tf( 1,[1, 0] ) ) ] * V_a
Out[0]:
NamedStateSpace{Continuous, Float64}
A = 
 0.0    6.25     0.0
 0.0  -10.0      3.2
 0.0   -0.3125  -4.0
B = 
 0.0
 0.0
 0.5
C = 
 0.0  6.25  0.0
 1.0  0.0   0.0
D = 
 0.0
 0.0

Continuous-time state-space model
With state  names: ##x#239 xH2##feedback#227 xH1##feedback#227
     input  names: Va
     output names: ##y#2411 ##y#2412

Задаем матрицы весов Q и R, и синтезируем контроллер с помощью функции lqr.

In [ ]: 
Q = [ 20 0 0; 0 1 0; 0 0 1 ]
R = 0.01
K_lqr = lqr( dc_aug, Q, R )
Out[0]:
1×3 Matrix{Float64}:
 44.7214  25.5262  14.1526

Затем получим замкнутую систему.

Добавим выход x, используя add_output(). Но для этого нам необходимо, чтобы переменная dcm имела тип данных StateSpace, как это требует функция add_output(). Поэтому делаем преобразование с помощью ss().

In [ ]: 
dcm_new = add_output(ss(dcm), I(2))
Out[0]:
StateSpace{Continuous, Float64}
A = 
 -10.0      3.2
  -0.3125  -4.0
B = 
 0.0  8.0
 0.5  0.0
C = 
 6.25  0.0
 1.0   0.0
 0.0   1.0
D = 
 0.0  0.0
 0.0  0.0
 0.0  0.0

Continuous-time state-space model

Добавим интегрирующее звено.

In [ ]: 
C = K_lqr * append( tf(1, [1, 0]), tf(1), tf(1) )
Out[0]:
TransferFunction{Continuous, ControlSystemsBase.SisoRational{Float64}}
Input 1 to output 1
44.72135954999597
-----------------
      1.0s

Input 2 to output 1
25.526213567574707
------------------
       1.0

Input 3 to output 1
14.152551403054153
------------------
       1.0

Continuous-time transfer function model

Описание разомкнутой системы управления с LQR.

In [ ]: 
OL = dcm_new * append( C, ss(1) )
Out[0]:
StateSpace{Continuous, Float64}
A = 
 -10.0      3.2  0.0
  -0.3125  -4.0  2.795084971874748
   0.0      0.0  0.0
B = 
 0.0   0.0                0.0                8.0
 0.0  12.763106783787354  7.076275701527076  0.0
 8.0   0.0                0.0                0.0
C = 
 6.25  0.0  0.0
 1.0   0.0  0.0
 0.0   1.0  0.0
D = 
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0

Continuous-time state-space model

Описание замкнутой системы управления с LQR.

In [ ]: 
CL = feedback( OL, I(3), U1=1:3, Y1=1:3 )
Out[0]:
StateSpace{Continuous, Float64}
A = 
 -10.0                  3.2                0.0
 -13.075606783787354  -11.076275701527077  2.795084971874748
 -50.0                  0.0                0.0
B = 
 0.0   0.0                0.0                8.0
 0.0  12.763106783787354  7.076275701527076  0.0
 8.0   0.0                0.0                0.0
C = 
 6.25  0.0  0.0
 1.0   0.0  0.0
 0.0   1.0  0.0
D = 
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0

Continuous-time state-space model

Передаточная функция (w_ref,Td)$\to$ w

In [ ]: 
cl_lqr = CL[ 1, 1:3:4 ]
Out[0]:
StateSpace{Continuous, Float64}
A = 
 -10.0                  3.2                0.0
 -13.075606783787354  -11.076275701527077  2.795084971874748
 -50.0                  0.0                0.0
B = 
 0.0  8.0
 0.0  0.0
 8.0  0.0
C = 
 6.25  0.0  0.0
D = 
 0.0  0.0

Continuous-time state-space model

Наконец, сравним три схемы управления ДПТ, построив графики выходных сигналов.

In [ ]: 
h_3 = lsim( cl_lqr, u, t )
plot( [h_1, h_2, h_3], label=["Прямое управление, h_1(t)" "Управление с обратной связью, h_2(t)" "Регулирование LQR, h_3(t)"] )
plot!( t, Td, label = "Внешний возмущающий моомент, Td" )
Out[0]:

Анализируя график можно заметить, что пики выходного сигнала стали меньше по сравнению с предыдущим способом управления.

Вывод

В данном примере было рассмотрено создание модели объекта управления - двигателя постоянного тока. Проведено сравнение трех методов управления ДПТ. В результате анализа полученных откликов системы, способ управления с LQR оказался наиболее эффективным и лучше всего боролся с воздействием внешнего возмущающего момента.

Файлы
dc_demo.ngscript

Тип

Интерактивные скрипты

Краткое описание

Создадим математического описания объекта управления - ДПТ. Разберем, как описать систему с несколькими входными сигналами. Рассмотрим способы управления.

Связанные материалы

Пусто

Теги

Категории

Отраслевые применения
Управление в технических системах

Языки

  • Julia

Форматы

    ngscript

Уровень

    Средний

Статус

Создано

Обновлено

Источник

Сообщество