Уравнение Шрёдингера
]add Plots, Roots, FFTW
using Plots
gr();
Нестационарное уравнение Шрёдингера
Это времезависимое уравнение Шрёдингера, и оно описывает эволюцию волновой функции для изолированной квантовой системы во времени. т.е. если дать начальное условие , и проинтегрировать данное уравнение, то мы получим ответ на то, что станет (или что было) с волновой функцией в момент времени t.
С математической точки зрения — это дифференциальное уравнение в частных производных, которое имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи.
С физической точки зрения, согласно уравнению Шредингера волновая функция изменяется детерминировано, то есть совершенно однозначно. В этом смысле квантовая механика напоминает классическую, в том смысле, что эволюция системы заранее предопределена начальными условиями. Однако сама волновая функция имеет вероятностный смысл.
- гамильтониан, это оператор полной энергии системы, то есть, сумма кинетической энергии и инергии системы в поле некоего потенциала .
Допустим, гамильтониан не зависит явно от времени и движение происходит только по одной координате, тогда:
Волновую функцию можно факторизовать на две функции от соответствующих переменных , что позволяет выделить разбить уравнение Шрёдингера на два выражения:
Второе уравнение есть ни что иное, как задача на собственные значения оператора Гамильтона (оператора энергии), то есть на допустимые наблюдаемые значения энергии и на соответствующие им состояния системы . Данное уравнение называется стационарным уравнением Шрёдингера, и оно даёт все возможные состояния консервативной системы.
Электрон в одномерной бесконечно глубокой потенциальной яме
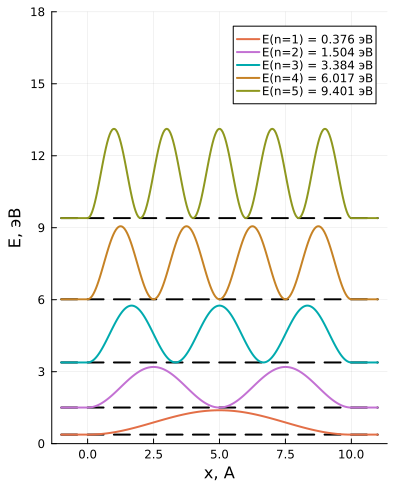
Рассмотрим простейшую квантовую систему: одномерный объект зажатый между бесконечными потенциальными барьерами - областями пространства, для нахождения в которых системе нужно иметь большое значение энергии. В области между стенками волновая функция подчиняется стационарному уравнению Шредингера:
Получили дифференциальное уравнение для гармонического осциллятора имеющее решение:
где - константы.
Граничные условия для стенки шириной имеют вид:
Для данных начальных условий и из нормировки волновой функции решение стационарного уравнения Шрёдингера примет вид:
Зададим основные константы и выведем значения энергии характерные для квантовой системы в разных состояниях и при разных значениях ширины ямы.
const ħ = 6.582119569e-16 # eV*s
const m = 9.1094e-31 # kg
const q = 1.6022e-19 # Kl
const l = 1e-10 # m -> Angstrom
const c = 2.99792458e8 # m/s
const C = m/ħ^2 * l^2/q # -> eV and A
nrg(N, L) = [ 0.5(n*π/L)^2 / C for n = 1:N ]
nn = 5
[ "No." "10 A" "20 A" "30 A"
1:nn nrg(nn, 10) nrg(nn, 20) nrg(nn, 30) ]
Зададим функции для красивой отрисовки графиков
function norminator(xs, psi, E, n)
dx = step(xs)
Y = abs2.(psi)
#println(sum(Y)*dx)
dE = E[n+1]-E[n]
Y /= maximum(Y)
Y *= 0.9dE
Y .+= E[n]
end
function analit_solut(xs, n, L = 10)
k = π*n/L
[ (0<x<L ? sqrt(2/L)*sin(k*x) : 0.0) for x in xs ]
end;
N = 256;
nn = 5
L = 10
X = range(-0.1L, 1.1L, N);
E1 = nrg(nn+1, L)
plot(xlab = "x, A", ylab = "E, эВ", ylim = (0,18))
for n = 1:nn
probs = norminator( X, analit_solut(X, n, L), E1, n )
plot!( [X[1], X[end]], [E1[n], E1[n]], line = (2, :dash, :black), lab = "" )
plot!(X, probs, lab = "E(n=$n) = $(round(E1[n], digits = 3)) эВ", line = 2)
end
plot!(size = (400, 500) )
Несмотря на простоту и даже примитивность эта идеализированная модель качественно и количественно воспроизводит поведение некоторых реальных систем. Например -электрон в углеродной цепочке тиакарбоцианина ведет себя как частица в бесконечной потенциальной яме.

Если задать размеры ямы исходя из геометрии молекулы и найти разности между соответствующими уровнями энергии, то можно получить длины волн совпадающие с полученным из экспериментов спектром, характерным для данного вещества:
Why the Particle-in-a-Box Model Works Well for Cyanine Dyes but Not for Conjugated Polyenes
a = 0.249e-9 # m
b = 0.567e-9 # m
h = 6.626e-34 # J*s
Lf(k) = a*(k+1)+b # ширина ямы
dE(n, k) = (n^2 - (n-1)^2)*h^2 / (8m*Lf(k)^2)
lam(n, k) = round( h*c/dE(n, k) * 1e9, digits = 2 )
lam(4,0), lam(5,1), lam(6,2), lam(7,3) # длина волны в нанометрах
Туннелирование электрона через потенциальную стенку
Метод матриц переноса
При решении задач о движении электронов в слоисто-неоднородных средах решения
уравнения Шредингера записываются отдельно в каждой из областей, где потенциал постоянен, в виде суперпозиции падающей и отраженной волн де Бройля, а для нахождения амплитуд этих волн используются граничные условия на интерфейсах между слоями. Такой подход позволяет легко формализовать расчет амплитуд волн де Бройля и коэффициентов отражения и прохождения в многослойных средах с использованием метода матриц переноса.
Для структуры состоящей из N слоев можно выписать решения стационарного уравнения Шредингера для каждой области:
Граничные условия:
Подставляя общее решение в условия на границах получаем СЛАУ относительно и :
или в матричном виде:
Таким образом, получена матрица передачи волны де Бройля из области k в область k+1.
С учетом того, что в области N+1 нет отраженной волны де Бройля и принимая во внимание рекурентное соотношение, можем найти связь между областями k = 0 и k = N+1 (границами всей структуры):
– матрица передачи волны де Бройля через всю слоистую структуру. Коэффициенты отражения и прохождения электронной волны через
структуру могут быть выражены через элементы передаточной матрицы следующим образом:
using Plots
plot([0,0], [0,1.5], line = (:arrow, 1, :black), annotations=(0.05, 1.5, text("U(x)", :left)) )
plot!([-0.5,1], [0,0], line = (:arrow, 1, :black), annotations=(1, 0.08, text("x", :up)))
plot!([-0.4,0,0,0.2,0.2,0.4,0.4,0.6,0.6,1], [0.2,0.2,1,1,0.2,0.2,1,1,0.2,0.2],
line = ( 3, :black), leg=false, ticks=nothing, border=:none )
annotate!([(-0.05, 0.25, text("U₀", :right)),
(0.1, 0.1, text("a₁", :center)),
(0.5, 0.1, text("a₂", :center)),
(-0.05, 1, text("U₁", :right)),
(0.3, 0.1, text("b", :center)) ])
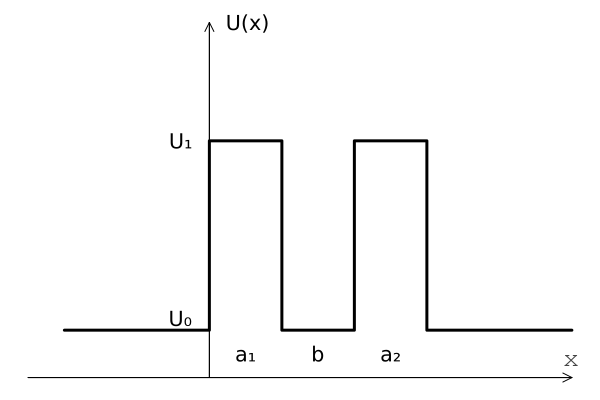
Рассмотрим прохождение частицы через систему из двух потенциальных барьеров, разделенных квантовой ямой, заключенную между двумя полубесконечными областями. Как и прежде, будем считать, что источник электронов находится в области 0 и бесконечно удален от структуры. Электрон движется от источника в положительном направлении оси Ox, обладая энергией E. Для расчета коэффициента прохождения электрона и амплитуд волн де Бройля воспользуемся матричным методом:
- число слоёв в структуре N = 3;
- число границ в рассматриваемой системе N+1 = 4;
- число областей, в которых потенциал U(x) постоянен N+2 = 5
Используем заточенность Julia под функциональное программирование:
a+b == +(a,b) # true
foo(s) = s(5,8)
foo(+)
13
foo(-)
-3
foo(^)
390625
чтобы упростить запись передаточной матрицы:
k(E) = sqrt(2m*q*Complex(E))/ħ/q # 1/m
function T_k(En, j)
γ_k = k(En-U[j])
γ_kp1 = k(En-U[j+1])
t(s1,s2,s3) = s1(1., γ_k/γ_kp1) * exp( im*x[j]*( s2(γ_kp1)+s3(γ_k) ) )
0.5*[t(+,-,+) t(-,-,-)
t(-,+,+) t(+,+,-)]
end;
a = [0., 0.4nm, 0.5nm, 0.4nm ] # толщины слоёв
U = [0., 8., 0., 8., 0.] # высоты барьеров
x = cumsum(a); # координаты границ раздела сред
function DandR(N::Int64, Es = 0., Ef = 6.)
function coefts(En)
γ_Np1 = En-U[N+1] |> k |> real
γ_0 = En-U[1] |> k |> real
Tm = prod(j-> T_k(En, j), N:-1:1) # mult matrices
Rn = abs2( Tm[2,1]/Tm[2,2] )
Dn = abs2( Tm[1,1] - Tm[1,2]*Tm[2,1] / Tm[2,2] ) * γ_Np1 / γ_0
[Rn Dn]
end
#find_zero( e-> coefts(e)[2]-1., 7.3 ) |> println
de = 0.005*(Ef-Es)
e = [Es:de:Ef;]
# из массива пар слепит массив с двумя столбцами:
RD = vcat(coefts.(e)...)
plot(e, RD[:,1], line = 3, lab = "отражение")
plot!(e, RD[:,2], line = 3, lab = "прохождение")
#vline!([U[2]], lab = "")
title!("Вероятность прохождения и отражения")
xaxis!("E, эВ")
end;
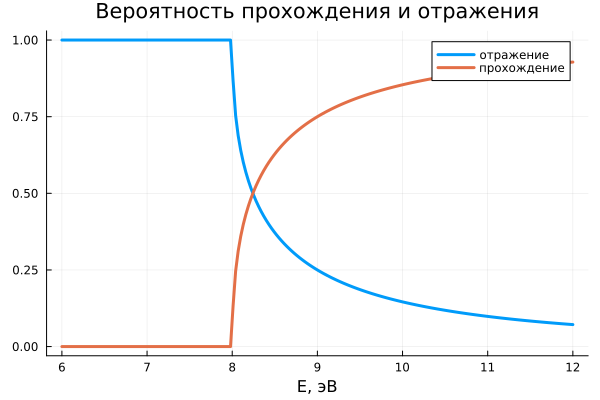
DandR(1, 12) # туннелирование через стенку
DandR(2, 12) # через барьер
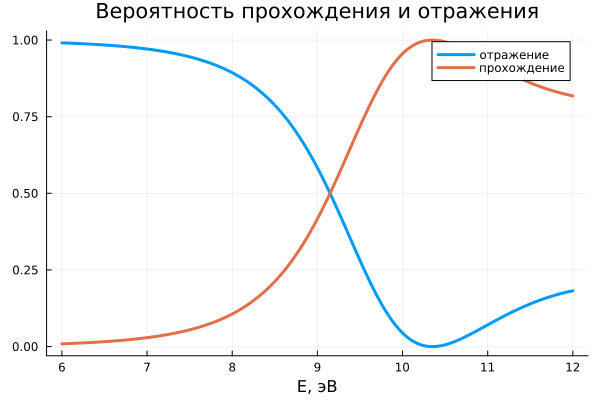
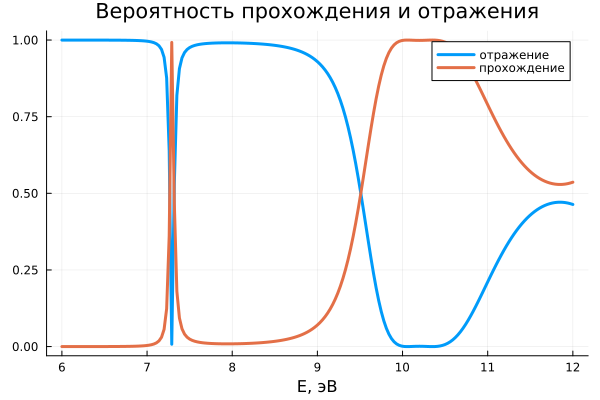
DandR(4, 12) # через двухбарьерную структуру
При эВ коэффициент прохождения D = 1, это явление называется резонасным туннелированием через структуру.
А теперь займемся волновыми функциями:
# значения энергии, кол-во границ, нормировочный коэффициент, левая граница по Х, правая, верхняя по У
function Ψ(E::Array{Float64,1}, N::Int64; A1 = 0.5, xl = -4a[2], xr = 2x[end], yup = 4.)
YU = repeat(U[1:N+1], inner=2) # чтоб рисовать правильно
XU = repeat(x[1:N], inner=2)
pushfirst!(XU, xl)
push!(XU, xr)
# рисуем стенки
plot(XU/nm, YU, lab = "", line = 2)
Xvec = copy(x[1:N])
pushfirst!(Xvec, xl)
push!(Xvec, xr)
Xarr = [ [Xvec[i]:0.005(Xvec[i+1]-Xvec[i]):Xvec[i+1];] for i = 1:N+1 ]
# массив массивов; каждый - это отрезок на ОХ
Xgrid = vcat(Xarr...) # объединить в один массив
function ψ(En)
γ = k.(En .- U)
Tms = [T_k(En, j) for j = 1:N] # Transfer matrices
TN = prod(Tms[N:-1:1]) # через всю структуру
ABs = zeros(Complex, N+1, 2)
ABs[1] = 1. # A_1
ABs[1,2] = -TN[2,1]/TN[2,2]*ABs[1] # B_1
ABs[end,1] = ( TN[1,1] - TN[1,2]*TN[2,1] / TN[2,2] ) * ABs[1] # A_last
ABs[end,2] = 0. # B_last
for i = 1:N-1
ABs[i+1,:] = Tms[i] * ABs[i,:]
end
# ищем ВФ на каждом отрезке
# todo: много промежуточных массивов
ψi(i) = ABs[i,1]*exp.(im*γ[i]*Xarr[i]) + ABs[i,2]*exp.(-im*γ[i]*Xarr[i])
real.( vcat(ψi.( [1:N+1;] )...) ) # возвращает Psi по всей структуре
end
hline!(E, lab = "") # уровни энергии
for En in E
Y = ψ(En)
#Y /= maximum(Y) # нормируем на единицу
Y .+= En
plot!(Xgrid/nm, Y, line = 3, lab = "E = $En eV" )
end
yaxis!("E, eV", (0, yup ) )
xaxis!("x, nm")
end;
a = [0., 0.3nm, 0.5nm, 0.3nm ] # толщины слоёв
U = [0., 12., 0., 12., 0.] # высоты барьеров
x = cumsum(a); # координаты границ раздела сред
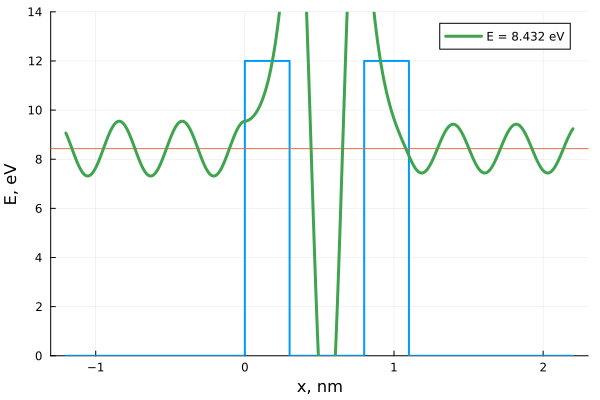
Ψ([8.432], 4, yup = 14) # туннелирование на резонансе
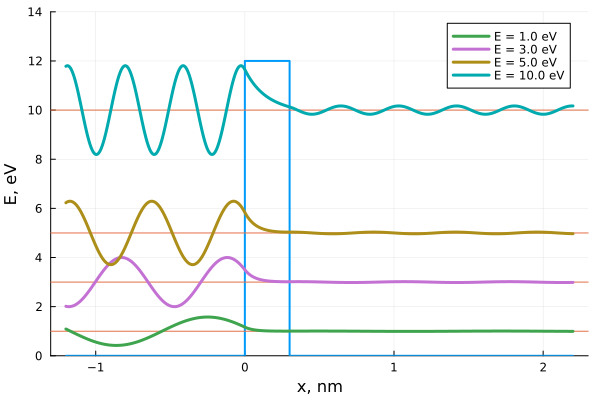
Ψ([1., 3.0, 5., 10.0], 2, yup = 14)
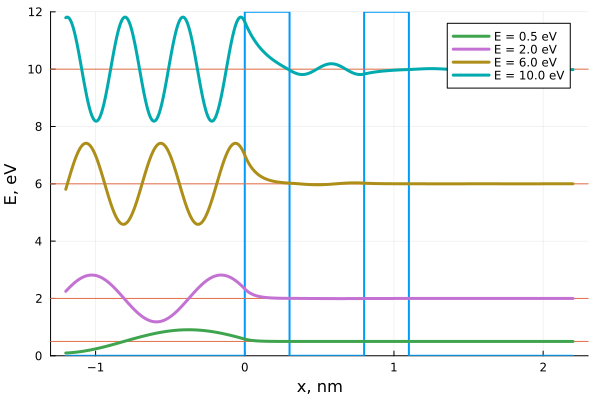
Ψ([0.5, 2., 6., 10.], 4, yup = 12)
Таким образом можно строить волновые функции для различный состояний квантовой системы при различных конфигурациях потенциальных барьеров. Явление квантового туннелирования используется в основе многих современных электронных устройств и чуть менее чем повсеместно встречается в биохимии.
Квантовый гармонический осциллятор
Многие модели квантовой теории сводятся к гармоническому осциллятору с потенциалом
Уравнения Шредингера для такого потенциала также имеет аналитическое решение:
Оно выражено через полиномы Эрмита
Которые можно расчитать через рекурентную формулу
или через детерминант:
Hn(n, x) = sum( j-> (-1)^j*factorial(n)*(2x)^(n-2j)/factorial(j)/factorial(n-2j), 0:n÷2 )
# детерминант трехдиагональной матрицы
Htd(n::Int, x::Float64) =
2^(0.5n)*det( Tridiagonal(ones(n-1), fill(sqrt(2)*x,n), [1.0n-i for i=1:n-1] ) );
En(n, ωħ = 1.0) = (n + 0.5)*ωħ
function analit_solut(xs, n, ωħ = 1.0)
dx = step(xs)
N = length(xs)
x0 = sqrt(C*ωħ)
A = sqrt(x0) / sqrt( sqrt(pi)*(2^n)*factorial(n) )
return [ A * Hn(n, ξ) * exp(-0.5*ξ^2) for ξ in xs*x0 ]
end;
С другой стороны, задачу на собственные функции и собственные значения на языке julia не составит труда решить численно. Для этого вторую производную в гамильтониане можно представить в конечно-разностной форме:
Так что сравним численное решение с аналитическим
using LinearAlgebra, SparseArrays
function numeric_solut(xs, V)
dx = step(xs)
N = length(xs)
H = SymTridiagonal( ones(N), -0.5ones(N-1) )/dx^2 / C
Vm = diagm(V);
Ψ = eigvecs(H+Vm)
E = eigvals(H+Vm)
Ψ, E
end;
function norminator(psi, E, n)
Y = abs2.(psi)
#println(sum(Y)*dx)
dE = E[n+1]-E[n]
Y /= maximum(Y)
Y *= 0.9dE
Y .+= E[n]
end;
N = 128
X = range(-4pi, 4pi, N)
dx = step(X)
garmosc(x, ωħ = 1.0) = 0.5C*(x*ωħ)^2;
clrs = [:violet, :blue, :green, :magenta, :gray, :cyan, :purple];
nn = 7
freq = 1.2
E1 = En.(0:N, freq)
V = garmosc.(X, freq)
Psi, E2 = numeric_solut(X, V)
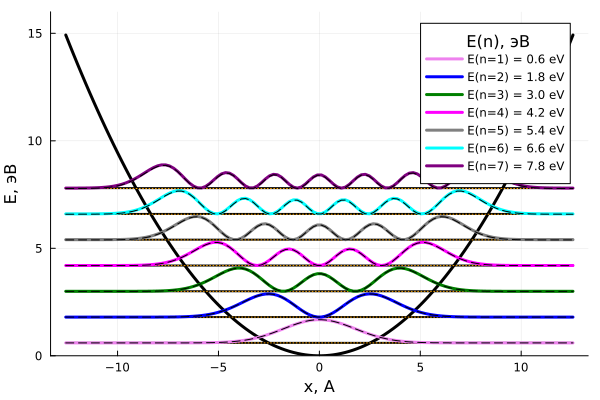
plot(xlab = "x, A", ylab = "E, эВ", legendtitle = "E(n), эВ", ylim = (0,16))
plot!(X, V, line = (3,:black), lab = "")
for n = 1:nn
probs1 = norminator( analit_solut(X, n-1, freq), E1, n )
probs2 = norminator( Psi[:, n], E2, n )
plot!( [X[1], X[end]], [E1[n], E1[n]], line = (2, :black), lab = "") # аналитическое
plot!( [X[1], X[end]], [E2[n], E2[n]], line = (1, :dot, :orange), lab = "")# численное
plot!(X, probs1, line = (3, clrs[n]), lab = "E(n=$n) = $(round(E1[n], digits = 3)) эВ")
plot!(X, probs2, line = (1, :dash, :black), lab = "") # численное
end
plot!()
Как видно, численные решения для собственных состояний и спектра гармонического осциллятора совпадают с аналитическими.
Таким образом, в данном файле приведен набор скриптов иллюстрирующих возможность использования языка julia и среды разработки Engee для проведения расчетов и выполнения качественных иллюстраций в процессе исследования на примере решения типовых задач из квантовой механики.