Выпуклая оболочка
Алгоритм построения выпуклой оболочки
Рассматриваем реализацию алгоритма построения выпуклой оболочки (convex hull) множества точек в двумерном пространстве на языке Julia.
Введение
Алгоритм построения выпуклой оболочки — это геометрический алгоритм, который находит минимальный выпуклый многоугольник, содержащий все заданные точки. Проще говоря, представьте, что у вас есть набор гвоздей на доске, и вы натягиваете вокруг них резинку — форма этой резинки и будет выпуклой оболочкой.
Этот алгоритм используется во многих областях: компьютерной графике, распознавании образов, оптимизации, робототехнике и других. В данном примере мы используем библиотеку Polyhedra.jl для работы с многогранниками, а именно с V-представлением точек (Vertex representation), чтобы построить выпуклую оболочку точек.
Основная часть
Установка необходимых пакетов (если еще не установлены)
import Pkg; Pkg.add(["Polyhedra", "CDDLib"])
Подключение библиотек
Polyhedra — основная библиотека для работы с многогранниками
CDDLib — библиотека для вычислений с многогранниками через double description метод
using Polyhedra, CDDLib, Makie
Задаем набор точек в виде вершинного представления (V-representation).
Каждая точка — это координаты [x, y]
Dots = [
[16,3], [12,17], [0,6], [-4,-6], [16,6],
[16,-7], [16,-3], [17,-4], [5,19], [19,-8],
[3,16], [12,13], [3,-4], [17,5], [-3,15],
[-3,-9], [0,11], [-9,-3], [-4,-2], [12,10]
];
vrep — это функция, создающая объект Vertex Representation из списка точек
A = vrep(Dots)
Создание объекта многогранника из V-представления
Используется бэкенд CDDLib для выполнения всех вычислений
P = polyhedron(A, CDDLib.Library())
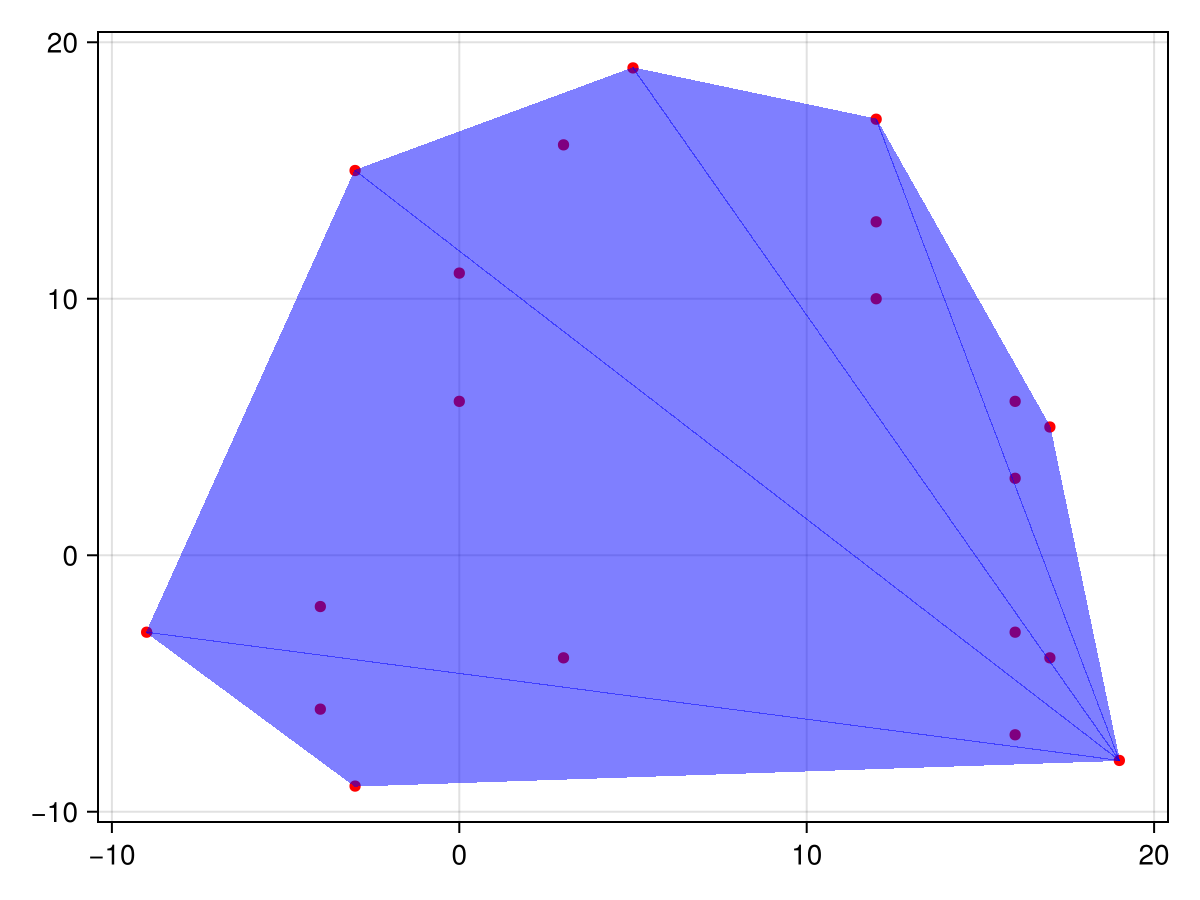
Построим точки и выпуклый многогранник:
# Создаем сетку (mesh) из многогранника P
m = Polyhedra.Mesh(P);
# Извлекаем координаты X и Y из вектора точек Dots
X = [dot[1] for dot in Dots] # Первые элементы - координаты X
Y = [dot[2] for dot in Dots] # Вторые элементы - координаты Y
# Создаем фигуру и оси для графика
fig = Figure()
ax = Axis(fig[1, 1])
# Рисуем точки на графике
Makie.scatter!(ax, X, Y, markersize=8, color=:red)
# Рисуем сетку многогранника полупрозрачным синим цветом
Makie.mesh!(m, color=(:blue,0.5))
# Отображаем фигуру
fig
Построение выпуклой оболочки многогранника P с самим собой (по сути — получаем ту же самую выпуклую оболочку)
Эта операция создает новый объект, представляющий выпуклую оболочку двух многогранников
Pch = convexhull(P, P)
Удаление избыточных точек/вершин из представления
То есть остаются только вершины, которые действительно нужны для описания границ выпуклого многоугольника
removevredundancy!(Pch)
Вывод результата на экран - информации о многограннике (вершины, ребра и т.д.)
println("$Pch")
Что происходит шаг за шагом?
- Мы задаем набор точек плоскости.
- Формируем по этим точкам V-представление — способ описания фигуры через ее вершины.
- Создаем объект типа "многогранник", который хранится во внутреннем формате библиотеки
Polyhedra. - Строим выпуклую оболочку (в данном случае фактически копируем её, так как объединяем многогранник с самим собой).
- Из полученного объекта удаляем избыточные точки — оставляем только те, что реально определяют границы фигуры.
- Печатаем результат: информация о вершинах выпуклого многоугольника будет выведена.
Заключение
Мы рассмотрели простой пример использования библиотеки Polyhedra.jl языка программирования Julia для построения выпуклой оболочки набора точек. Благодаря мощным возможностям этой библиотеки и поддержке различных бэкендов, можно легко строить, анализировать и визуализировать полиэдральные структуры. Это может быть полезно при решении задач из линейного программирования, компьютерной графики и аналитической геометрии.
Подводя итог, данный пример позволяет новичку понять принципы работы с геометрическими данными и многогранниками в Julia.
Пример разработан с использованием материалов Rosetta Code