Модельная схема

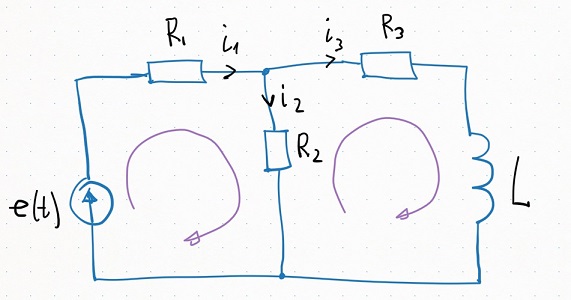Рассмотрим простую электрическую схему с одним реактивным элементом. Запишем уравнения, которые её описывают. Одно узловое уравнение и два контурных.

Перепишем уравнения, перегруппировав слагаемые.

Получилась дифференциально-алгебраическая система уравнений. Переменные , - алгебраические (от этих функций нет производных), переменная входит в уравнения со своей производной.

Когда я был студентом, мне рассказывали, что необходимо выразить токи , через ток и получить дифференциальное уравнение на функцию . Да, действительно, это можно сделать.

После таких выражений для токов

Получим ОДУ на

Примечательно следующее: результатом численного интегрирования дифференциального уравнения на будут примерные (так как решение численное) значения этой функции на определенной сетке . Далее по этим значениям и уравнениям, записанным выше, мы найдем примерные значения оставшихся токов , . И, так как, мы использовали для нахождения алгебарических переменных , уравнения, которые их связывают, то естественным образом эти уравнения строго выполняются для сеточных примерных значений.

Значения всех токов на сетке получены с погрешностью, но соотношения между токами выполняются точно. Получается, что верным равенством является не только:

Но и:

А это для практики уже принципиально полезное свойство.

А что если не выражать?

В этом примере, я утверждал, что задачи такого типа также можно решать как дифференциально-алгебраическую систему уравнений сразу "в лоб", без предварительного выражения переменных друг через друга (да и это может быть очень трудоемко для настоящих больших систем). То есть сеточные значения токов будут получаться одновременно в процессе численного решения системы.

Возникает вопрос, а что будет с соотношениями между токами в таком случае?

Давайте посмотрим в общем виде и на текущем примере.

Записанная выше система уравнений является простейшим видом дифференциально-алгербраической системы уравнений - полуявная индекса 1 (semi-explicit DAE index 1).

где - вектор дифференциальных переменных;
- вектор, алгебраических переменных.

В нашем случае:

Будем решать нашу систему неявными методами: Эйлера, средней точки, трапеций.

Неявный метод Эйлера

Таблица Бутчера (Butcher tableau) имеет вид:

В левом столбце будем писать уравнения в общем виде, а в правом для рассматриваемой схемы.

где красным цветом отмечены неизвестные значения в k+1 момент времени, зеленым известные в k-ый момент; , с - шаг интегрирования.

Мы получили линейную систему алгебраических уравнений (в общем случае система может быть нелинейной) на величины всех трех токов в k+1 момент времени. Важным является обстоятельство, что второе и третье уравнение в правом столбце содержат корректно записанные уравнения по первому и второму законам Кирхгофа в k+1 момент времени. Решением этой системы будут значения, которые все уравнения превращают в равенства, то есть неявный метод Эйлера позволяет точно сохранять алгебраические соотношения между численно найденными значениями.

Неявный метод средней точки (Midpoint)

Таблица Бутчера имеет вид

Уравнения для нахождения сеточных значений:

Посмотрим внимательно на второе уравнение правого столбца. Если начальные условия на токи выбраны так, что алгебраическая сумма токов в узле равна нулю , то из уравнения следует, что и в любой следующий момент времени сумма токов также будет равна нулю. Алгебраическое соотношение на токи выполняется и при таком численном методе. Правда здесь это является свойством уравнения, а не свойством метода.

Посмотрим на третье уравнение. Оно показывает, что сумма напряжений по контуру будет равна сумме ЭДС только в момент времени средний между точками k и k+1 расчетной сетки. Но эти значения нас не сильно интересуют. Мы решаем систему на конкретной сетке и значения между узлами представляют второстепенный интерес. Заключаем что, хотя токи и согласованы между собой, напряжения в контуре уже не сбалансированы.

Неявный метод трапеций

Таблица Бутчера имеет вид

Уравнения для нахождения сеточных значений:

По сравнению с предыдущим методом третье уравнение изменилось. Теперь, если в нулевой момент времени, токи были выбраны так, чтобы второй закон Кирхгофа выполнялся, то он будет выполняться и в последующие моменты времени, так как скобки с известными (зелеными) с предыдущего временного шага значениями равны нулю.

Таблицы Бутчера

Если посмотреть на таблицы Бутчера, то видно, что хорошим свойством, сохранять алгебраические связи обладают методы у которых две нижние строки одинаковы (нижняя строка матрицы и вектор коэффициентов , обозначения можно посмотреть здесь). И, действительно, это одно из необходимых условий для того чтобы метод интегрирования назывался жестко точным (stiffly accurate).

Численный пример

Решим исходную систему всеми тремя способами и посмотрим на точность выполнения алгебраических соотношений.

using DifferentialEquations, LinearAlgebra;

# Ввод параметров электрической цепи
R1 = 10.0
R2 = 15.0
R3 = 20.0
f  = 50.0
L = 15e-3

# Определение дифференциально-алгебраической системы
function circuitDAEsemiexplicit(dy, y, p, t)
    R1, R2, R3 = p
    i1, i2, i3 = y

    U = 100 * sin(2 * π * 50 * t) * exp(-t/0.03)
    
    dy[1] = i2*R2 - i3*R3
    dy[2] = -i1 + i2 + i3
    dy[3] = i1*R1 + i2*R2 - U
    
    return nothing
end

# mass matrix
M = Diagonal([L, 0, 0])

# Начальные условия для y
y0 = zeros(3)

# Диапазон времени для расчета, пусть будет два периода промышленной частоты 50 Гц
tspan = (0.0, 0.04) 

# Задание параметров
paramsDAE = (R1, R2, R3)

# Создание объекта ODEProblem с передачей параметров
fn = ODEFunction(circuitDAEsemiexplicit, mass_matrix = M);
probDAEsemiexplicit = ODEProblem(fn, y0, tspan, paramsDAE);

# Решение дифференциальных уравнений
solDAE_bEuler = solve(probDAEsemiexplicit, ImplicitEuler(), adaptive=false, dt=0.001)
solDAE_Mid = solve(probDAEsemiexplicit, ImplicitMidpoint(), adaptive=false, dt=0.001)
solDAE_Trapz = solve(probDAEsemiexplicit, Trapezoid(), adaptive=false, dt=0.001)

t = solDAE_bEuler.t
u = 100 * sin.(2 * π * 50 * t) .* exp.(-t/0.03)

# Выбираем переменные для сравнения
i1_sol_bEuler = [v[1] for v in solDAE_bEuler.u];
i2_sol_bEuler = [v[2] for v in solDAE_bEuler.u];
i3_sol_bEuler = [v[3] for v in solDAE_bEuler.u];

i1_sol_Mid = [v[1] for v in solDAE_Mid.u];
i2_sol_Mid = [v[2] for v in solDAE_Mid.u];
i3_sol_Mid = [v[3] for v in solDAE_Mid.u];

i1_sol_Trapz = [v[1] for v in solDAE_Trapz.u];
i2_sol_Trapz = [v[2] for v in solDAE_Trapz.u];
i3_sol_Trapz = [v[3] for v in solDAE_Trapz.u];

# Абсолютные погрешности выполнения алгебраических уравнений
d1_Euler = abs.(-i1_sol_bEuler + i2_sol_bEuler + i3_sol_bEuler);
d1_Mid = abs.(-i1_sol_Mid + i2_sol_Mid + i3_sol_Mid);
d1_Tr = abs.(-i1_sol_Trapz + i2_sol_Trapz + i3_sol_Trapz);

d2_Euler = abs.(i1_sol_bEuler*R1 + i2_sol_bEuler*R2 - u);
d2_Mid = abs.(i1_sol_Mid*R1 + i2_sol_Mid*R2 - u);
d2_Tr = abs.(i1_sol_Trapz*R1 + i2_sol_Trapz*R2 - u);

p1 = plot(t, [i3_sol_bEuler i3_sol_Mid i3_sol_Trapz],
    lw=3,
    label = ["Ток i3 Euler" "Ток i3 Mid" "Ток i3 Trapz"],
    title = "Токи через катушку разными методами")
display(p1)

Токи плюс/минус выглядят одинаково. С учетом довольно большого шага интегрирования значения выглядят нормально. Посмотрим как токи согласуются между собой в части суммы токов в узле и суммы напряжений по контуру.

p2 = plot(t, [d1_Euler d1_Mid d1_Tr],
    lw=3,
    label = ["1з Кирхгофа Euler" "1з Кирхгофа - Mid" "1з Кирхгофа - Trapz"],
    title = "Погрешность по первому алг. уравнению (1-й з-н Кирхгофа)")
p3 = plot(t, [d2_Euler d2_Mid d2_Tr], lw=3,
    label = ["2з Кирхгофа Euler" "2з Кирхгофа - Mid" "2з Кирхгофа - Trapz"],
    title = "Погрешность по второму алг. уравнению (2-й з-н Кирхгофа)")
display(p2)

Погрешности выполнения первого алгебраического ограничения очень малые и обусловлены неточностью операций с числами с плавающей запятой.

display(p3)

Погрешность выполнения второго алгебраического уравнения при расчете методом средней точки на много порядков выше, чем у жестко точных методов. Масштабы несопоставимы, поэтому погрешность жестко точных методов представляется "нулевой" линией.

Понятно, что если к уравнению

добавить слагаемое, например, дополнительный источник тока

то погрешность метода средней точки резко вырастет и на этом уравнении.

Выводы

Видно насколько сильно отличается погрешность соблюдения контурного уравнения в зависимости от метода;
При уменьшении шага погрешность будет уменьшаться, но жестко точные методы на любом шаге "из коробки" имеют очень хорошее свойство для дифференциально-алгебраических систем.

Заметка по решению систем ДАУ

Модельная схема

А что если не выражать?

Неявный метод Эйлера

Неявный метод средней точки (Midpoint)

Неявный метод трапеций

Таблицы Бутчера

Численный пример

Выводы

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник