Запуск FMI модели в Engee

Запускаем FMU-модели в окружении Julia чтобы получить результаты симуляции и использовать их в дальнейших вычислениях.

Описание задачи

Стандарт FMI (Functional Mockup Interface) подразумевает упаковку модели в файл FMU (Functional Mockup Unit), содержащий либо набор уравнений, либо код, моделирующий систему (предположительно, поддерживаются различные языки программирования, которые можно вызвать в Engee: Python, Java, Fortran, C++ и т.д. включая Julia).

Для примера рассмотрим модель пружины и маятника, собранной в Dymola. Чтобы ее запустить нам потребуется библиотека FMI.jl и набор учебных моделей, которые собраны в пакете FMIZoo.jl.

Pkg.add( ["FMI", "FMIZoo"] )

Подключим установленные библиотеки:

using FMI
using FMIZoo

Мы собираемся провести симуляцию такой модели:

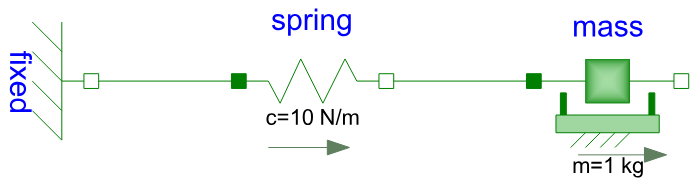
Библиотека FMI.jl позволяет запускать FMI/FMU-модели несколькими способами, и мы покажем два из них:

• через команду simulate
• через создание собственного цикла симуляции и команду fmi2DoStep.

Создадим временной вектор (зададим начало tStart, окончание Stop симуляции и временной шаг tStep):

tStart = 0.0
tStep = 0.1
tStop = 8.0
tSave = tStart:tStep:tStop

0.0:0.1:8.0

Простейший сценарий запуска FMU модели

Загрузим модель SpringFrictionPendulum1D из пакета моделей FMIZoo.jl.

fmu = loadFMU( "SpringFrictionPendulum1D", "Dymola", "2022x" )
info(fmu)

#################### Begin information for FMU ####################
	Model name:			SpringFrictionPendulum1D
	FMI-Version:			2.0
	GUID:				{2e178ad3-5e9b-48ec-a7b2-baa5669efc0c}
	Generation tool:		Dymola Version 2022x (64-bit), 2021-10-08
	Generation time:		2022-05-19T06:54:12Z
	Var. naming conv.:		structured
	Event indicators:		24
	Inputs:				0
	Outputs:			0
	States:				2
		33554432 ["mass.s"]
		33554433 ["mass.v", "mass.v_relfric"]
	Parameters:			12
		16777216 ["fricScale"]
		16777217 ["s0"]
		16777218 ["v0"]
		16777219 ["fixed.s0"]
		...
		16777223 ["mass.smin"]
		16777224 ["mass.v_small"]
		16777225 ["mass.L"]
		16777226 ["mass.m"]
		16777227 ["mass.fexp"]
	Supports Co-Simulation:		true
		Model identifier:	SpringFrictionPendulum1D
		Get/Set State:		true
		Serialize State:	true
		Dir. Derivatives:	true
		Var. com. steps:	true
		Input interpol.:	true
		Max order out. der.:	1
	Supports Model-Exchange:	true
		Model identifier:	SpringFrictionPendulum1D
		Get/Set State:		true
		Serialize State:	true
		Dir. Derivatives:	true
##################### End information for FMU #####################

Запустим расчет этой модели, указав начало и конец времени симуляции и сохраняемую переменную mass.s. Поскольку в модели есть трение, колебания происходят со снижающейся амплитудой, а спустя некоторое время груз приходит в состояние покоя.

simData = simulate(fmu, (tStart, tStop); recordValues=["mass.s"], saveat=tSave)
plot( simData )

После окончания расчета нужно выгрузить из памяти модель FMU и удалить все временные данные.

unloadFMU(fmu)

Создание собственого цикла симуляции

В более сложном случае, например когда вам нужно связать работу сразу нескольких моделей, можно организовать расчетный цикл, в котором модель будет осуществлять шаги в своем фазовом пространстве вдоль по некоторому временному вектору.

Загрузим модель FMU:

fmu = loadFMU("SpringFrictionPendulum1D", "Dymola", "2022x")

Model name:	SpringFrictionPendulum1D
Type:		1

Функция шага ожидает специально подготовленную модель (конкретную реализацию), которую мы создадим при помощи fmi2Instantiate. Таким образом можно из одного FMU файла инициализировать сразу много моделей.

instanceFMU = fmi2Instantiate!(fmu)

FMU:            SpringFrictionPendulum1D
    InstanceName:   SpringFrictionPendulum1D
    Address:        Ptr{Nothing} @0x000000001d62f8c0
    State:          0
    Logging:        false
    FMU time:       -Inf
    FMU states:     nothing

В следующей ячейке мы осуществляем настройку эксперимента (fmi2SetupExperiment), где указываем начало и конец временного интервала для симуляции, затем модель нужно перевести в режим инициализации (fmi2EnterInitializationMode) и получить ее начальное состояние после инициализации (fmi2ExitInitializationMode).

fmi2SetupExperiment(instanceFMU, tStart, tStop)

fmi2EnterInitializationMode(instanceFMU) # установить исходное состояние
fmi2ExitInitializationMode(instanceFMU)  # прочитать исходное состояние

0x00000000

Теперь мы можем запустить модель в расчетном цикле. Функция fmi2DoStep с фиксированным шагом tStep позволяет осуществлять расчетные шаги этой модели. Если у модели есть входные параметры или принимаемые данные, их можно изменять в цикле.

values = []

for t in tSave
    # выставить входные параметры модели, если требуется
    # ...

    fmi2DoStep(instanceFMU, tStep)
    
    # сохранить выходы модели
    value = fmi2GetReal(instanceFMU, "mass.s")
    push!(values, value)
end

plot(tSave, values)

В окончание расчета мы должны освободить память и удалить промежуточные файлы.

fmi2Terminate(instanceFMU)
fmi2FreeInstance!(instanceFMU)
unloadFMU(fmu)

[OK][CvodeStatistics][SpringFrictionPendulum1D]: Sundials CVode Statistics
    Stop time                                : 8.00 s
    Simulation time                          : 1.42 s
    Number of external steps                 : 80
    Number of internal steps                 : 191
    Number of non-linear iterations          : 263
    Number of non-linear convergence failures: 0
    Number of f function evaluations         : 291
    Number of g function evaluations         : 339
    Number of Jacobian-evaluations (direct)  : 7
    Maximum integration order                : 5
    Suggested tolerance scale factor         : 1.0
    Grouping used                            : no

Заключение

Мы запустили простую FMU модель при помощи одной команды, а также разобрались, как организовать расчетный цикл, где можно было бы обновлять входные параметры модели и принимать оперативные решения на основе выходных данных.