Автоматическое формирование уравнений

Введение

Некоторые студенты электроэнергетических специальностей, когда делают расчетные задания по ТОЭ, задумываются о какой-то своей программке, которая бы считала не только одну схему, но и схемы всех вариантов преподавателя, а в идеале вообще любую схему.

Важный вопрос, который должен быть решен в рамках такой задачи это автоматическое составление системы уравнений (алгебраической для расчетов установившегося режима, дифференциально-алгебраической для расчетов переходных процессов), описывающих схему. А также перестройка этой системы в зависимости от добавления/удаления новых элементов.

Это не так просто, заставить компьютер сформировать определенную систему, так как могут начаться проблемы с поиском независимых узлов и/или контуров (в зависимости от метода). Проблемы с ветвями с нулевым сопротивлением, параллельным соединением источников эдс и так далее.

В моем случае в студенчестве я остановился на поделке которая решала только узкий круг необходимых именно в то время задач.

Один из способов

Один из вариантов составления уравнений дан в книге "Теоретические основы электротехники" (Демирчян К.С. Нейман Л.Р. Коровкин Н.В. Чечурин В.Л.).

Упрощенно: нужна матрица соединений (инцидентности), которая определяет топологию схемы. Очень важно, что ветви должны быть определены как ветви дерева графа и ветви связей (то есть нужно найти дерево графа). Имея такую отсортированную прямоугольную матрицу, можно получить уравнения по первому и второму законам Кирхгофа для независимых узлов и контуров. Контурные уравнения получаются после обращения матрицы размерность которой равна числу независимых узлов.

Еще один

Далее рассмотрим еще один пример составления уравнений, который часто используется в программах компьютерной симуляции и описан в диссертации (PhD thesis) "A Structured Model Language for Large Continuous Systems" by Hilding Elmqvist.

Всё завязано на отдельные элементы (и их уравнения) и связи между этими элементами.

Возьмем к примеру резистор “в вакууме”.

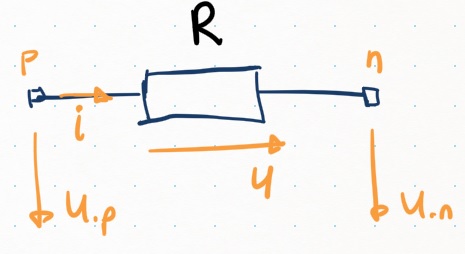
Введем для него ток , который протекает в условном положительном направлении, напряжение условно положительного контакта (positive), напряжение условно отрицательного контакта (negative) и напряжение на самом резисторе .

Можно написать следующие уравнения:

где - сопротивление резистора, Ом.

Если задуматься, то первое уравнение подходит для любого двухполюсника, а второе характеризует двухполюсник именно как резистор.

Получается что двухполюсник порождает 2 уравнения с 4-мя неизвестными.

Рассмотрим учебную схему

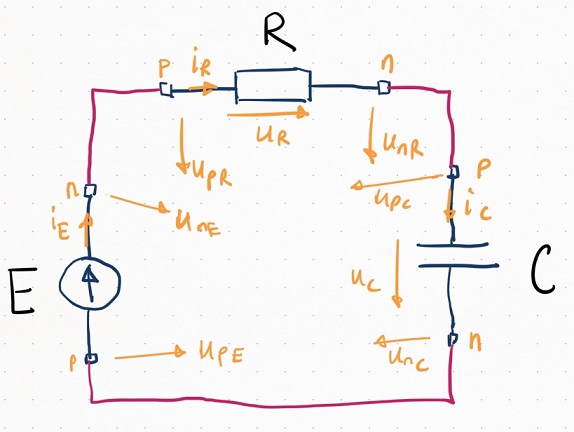Схема состоит из источника эдс, резистора и конденсатора. Далее будем писать уравнения и считать нарастающим итогом, сколько получается всего неизвестных и всего уравнений.

Уравнения элементов

Уравнения резистора:

Итого: 4 неизвестных, 2 уравнения

Уравнение конденсатора:

Итого: 8 неизвестных, 4 уравнения

Уравнения источника эдс:

На ток ничего не написать, потому что суть источника эдс как раз в том, чтобы держать на своих зажимах одинаковое напряжение независимо от тока.

Итого: 11 неизвестных, 5 уравнений

Уравнения связей

Начинаем соединять элементы. При соединениях элементов будут появляться новые уравнения.

Соединяем источник эдс с резистором:

Первое уравнение говорит нам о том, что соединительный провод не имеет сопротивления поэтому напряжения на зажимах одинаковые.

Второе уравнение это первый закон Кирхгофа для узла в котором сходится две ветви.

Итого: 11 неизвестных, 7 уравнений

Соединяем резистор с конденсатором:

Итого: 11 неизвестных, 9 уравнений

Соединяем конденсатор с источником эдс:

Итого: 11 неизвестных, 11 уравнений

Фуфф, получилось. Мы нашли все уравнения и их количество равно количеству неизвестных. Получилась система дифференциально-алгебраических уравнений (одно дифференциальное и десять алгебраических). Посмотрим целиком на всю систему.

Далее ее надо решать известными из математики методами (например, как здесь).

Problems?

Есть нюанс.. В системе линейно зависимые уравнения. А именно последние три уравнения на токи. Это прямое следствие того, что в схеме с N узлами независимыми являются максимум N-1. Очевидно, что из последних трех уравнений независимыми являются только 2. Такая система нам не нужна, поэтому убираем одно из уравнений, например .

Итого: 11 неизвестных, 10 уравнений

Решение

Мы получили недоопределенную систему уравнений (уравнений меньше чем неизвестных). В таких системах (если они имеют решение) можно свободным переменным задать определенные значения, а базисные выразить через них. Тогда получится бесконечное множество решений, параметризованное значением выбранных свободных переменных.

Возьмем к примеру и положим что оно равно , тогда всё получится, у нас станет 10 неизвестных и 10 уравнений, но как то всё неформально..

Лучше используем еще один элемент (reference) который сделает всё за нас.

Его уравнение:

Константа, естественно, может быть и нулевой.

Итого: 12 неизвестных (считаем неизвестным) и 11 уравнений.

И добавляем уравнение связи (еще одно уравнение в зависимости от того, куда подключен reference):

Итого: 12 неизвестных и 12 уравнений
Мы еще раз пришли к равенству уравнений и неизвестных, но на этот раз с корректной системой, которую действительно можно решить.

Завершение

Получается обязательность подключения элемента ref связана именно с тем, что у каждого двухполюсника есть напряжения и и они не определены без элемента ref. Они могут быть любыми лишь с тем ограничением, что их разность должна удовлетворять уравнению этого двухполюсника. На самом деле уже на этапе уравнения должен возникать вопрос "а относительно чего измеряются и ?", ведь напряжения всегда связывают две точки схемы, вот вторую точку и надо добавить вручную.

Но постойте - 12 уравнений? Для схемы с тремя элементами? Серьезно? Явно эта схема может быть описана проще.

Да это так, но несомненным плюсом изложенного метода является то, что он легко масштабируется на большие схемы. Также по мере вытаскивания элементов на холст - появляются уравнения элементов, а при связывании элементов между собой, появляются уравнения связей. И этот алгоритм сработает как для трех элементов, так и для трехсот. Плюс есть логическое разделение уравнений элементов и уравнений связей, что позволяет разрабатывать отдельные элементы и переиспользовать их в разных схемах.