БПФ и спектральный анализ с EngeeDSP

Продолжаем знакомиться с функционалом библиотеки EngeeDSP на примере задачи спектрального анализа и применения функции быстрого преобразования Фурье (БПФ).

Пример основан на данных ранее опубликованных проектов (БПФ, Спектральный анализ) которые выполнялись с применением подключаемых библиотек Julia, таких как DSP.jl, FFTW.jl, Statistics.jl и проч. В данном случае нет необходимости в подключении этих библиотек, так как их функционал покрывается EngeeDSP.

Ниже рассматриваются особенности применения функции fft для оценки амплитудного и фазового спектров тестового сигнала, а также практическая задача спектрального анализа для определения характеристик записанного аудиосигнала.

Функция FFT

Информацию о частотном и фазовом составе сигнала можно узнать при помощи перехода от временной области анализа к частотной методом преобразования Фурье. В качестве базового тестового сигнала сгенерируем сумму четырёх синусоид с разными амплитудами, основными частотами и начальными фазами:

fs = 1000;                              # частота дискретизации сигнала
dt = 1/fs;                              # период дискретизации
stoptime = 1;                           # время окончания сигнала
t = 0:dt:stoptime-dt;                   # вектор отсчётов времени
amplitude = [0.58 1.1 0.74 0.25];       # вектор четырёх амплитуд
f0 = [44 130 251 305];                  # вектор частот в Гц
phase_deg = [45 -135 90 60];            # вектор начальных фаз в градусах
phase = deg2rad.(phase_deg);            # вектор начальных фаз в радианах

four_sines = amplitude .* cos.(2*pi*t.*f0 .+ phase);
sum_sines = vec(sum(four_sines, dims = 2));
plot(t, sum_sines, title = "Сумма четырёх синусоид", xlim = (0, 0.15), legend = false,
                    xguide = "Время (с)", yguide = "Амплитуда")

Применим к сигналу функцию fft напрямую и визуализируем результат:

A = EngeeDSP.Functions.fft(sum_sines);
plot(A)

График отрисовывается на комплексной плоскости, так как комплексный вектор на выходе БПФ содержит информацию как об амплитуде составляющих, так и о фазе. Также стоит отметить, что количество комплексных отсчётов на выходе алгоритма соответствует количеству отсчётов сигнала во временной области на его входе.

Отобразим модуль комплексного вектора на выходе БПФ:

plot(abs.(A), xguide = "Номер отсчёт БПФ", yguide = "Модуль БПФ", legend = false)

Функция fftshift из состава EngeeDSP позволяет представить выход БПФ в привычном виде спектра, в нашем случае симметричного относительно центра - нулевой частоты. Но нам также придётся отложить по оси абсцисс вектор дискретных частот в пределах от до :

B = EngeeDSP.Functions.fftshift(A);
nsamp = length(t);
df = fs/nsamp;
println("Разрешение по частоте = ", df, "  Гц")
freq_vec = -fs/2:df:fs/2 - df;
plot(freq_vec, abs.(B), xguide = "Частота (Гц)", yguide = "Модуль БПФ", legend = false)

Разрешение по частоте = 1.0  Гц

Наконец, чтобы получить амплитудный спектр сигнала, нам необходимо учитывать количество отсчётов на выходе функции БПФ, а также принять во внимание, что энергетика вещественного сигнала также распространяется и на область отрицательных частот, которая, в нашем случае, неинформативна. Отобразим амплитудный спектр сигнала в области положительных частот линейчатым графиком, убедимся в корректности расчёта амплитуд синусоид на синтезируемых частотах:

S = 2*B/nsamp;
plot(freq_vec, abs.(S), line=:stem, marker=:circle, xlim=(0, 500),
        xguide = "Частота (Гц)", yguide = "Амплитуда",
        title = "Амплитудный спектр тестового сигнала")

Построим фазовый спектр тестового сигнала, определив "угол" отсчётов БПФ функцией angle. Отметим маркерами интересующие нас частотные компоненты, убедимся, что фаза рассчитана правильно:

idx = f0 .+ Int(fs/2 + 1);
plot(freq_vec, rad2deg.(angle.(S)), line=:stem, xlim=(0, 500),
        xguide = "Частота (Гц)", yguide = "Фаза (град)",
        title = "Фазовый спектр тестового сигнала")
scatter!(freq_vec[idx], rad2deg.(angle.(S[idx])), legend = false)

Постановка задачи для анализа

В качестве сигнала для анализа возьмём аудиозапись гитарной струны. Основная задача - определить, что за нота проигрывается, анализируя спектр сигнала. Загрузим численные отсчёты сигнала функцией wavread, которая также позволяет выделить частоту дискретизации сигнала fs - в нашем случае она равна 8000 Гц:

using WAV
audio_data, fs = wavread("guitar.wav");

Подсчитаем количество отсчётов сигнала во временной области, вычислим временной шаг, сформируем вектор времени и численный вектор отсчётов сигнала sig:

nsamples = length(audio_data);
dt = 1/fs;
t = 0:dt:(nsamples - 1) .* dt;
sig = vec(audio_data);

Для прослушивания аудио воспользуемся дополнительной функцией audioplayer:

using Base64
function audioplayer(s, fs);
    buf = IOBuffer();
    wavwrite(s, buf; Fs=fs);
    data = base64encode(unsafe_string(pointer(buf.data), buf.size));
    markup = """<audio controls="controls" {autoplay}>
                <source src="data:audio/wav;base64,$data" type="audio/wav" />
                Your browser does not support the audio element.
                </audio>"""
    display("text/html", markup);
end

audioplayer (generic function with 1 method)

Прослушаем звук колеблющейся струны:

audioplayer(sig,fs)

Отобразим колебания во временной области:

plot(t,sig, title = "Колебания струны во времени", 
        xguide = "Время (с)", yguide = "Амплитуда", legend = false)

Узнать основную частоту колебания по форме периодического сигнала во временной области можно, но всё же весьма затруднительно.

Оценка спектра сигнала

Построим спектр мощности аудиосигнала при помощи последовательности операций, применённых выше. Мы также будем оценивать спектр методом БПФ, но в этот раз ограничим число точек на выходе функции fft 8000 отсчётами.

Дальнейшие действия повторяют стандартный алгоритм - вычисление комплексного БПФ, сдвиг, нормировка по уровню. Но для отображения по оси ординат уже берётся квадрат амплитуды, т.е. мощность, и переводится в децибеллы:

nFFT = Int(fs);                         # кол-во отсчётов на выходе БПФ
A = EngeeDSP.Functions.fft(sig, nFFT);
B = EngeeDSP.Functions.fftshift(A);
S = (2*B)/nFFT;
df = fs/nFFT;
freq_vec = -fs/2:df:fs/2-df;
plot(freq_vec, 10log10.(abs.(S.^2)),
        xguide = "Частота (Гц)", yguide = "Мощность (дБ)",
        title = "Спектр мощности аудиосигнала", legend = false)

Мы наблюдаем спектр мощности аудиосигнала в пределах от -4000 Гц до 4000 Гц.

На спектре явно прослеживается гармоническая структура - равнорасположенные пики. Гармоники - это синусоидальные колебания, частоты которых кратны основной частоте .

- самая низкая частота в сигнале (первая гармоника), а высшие гармоники - частоты вида , где (вторая, третья и т. д.).

Определение основной частоты

Анализируя гармоники, можно определить основную частоту в спектре сигнала. Но для начала напишем пользовательскую функцию оценки спектра на основе применяемого алгоритма. В качестве дополнительных входных аргументов она будет принимать частоту дискретизации сигнала, количество отсчётов БПФ и флаг "одностороннего" спектра:

function fftspectrum(sig, fs; nfft = nothing, onesided = nothing)
    if nfft != nothing
        nsamples = nfft;
        sig = sig[1:nfft];
    else
        nsamples = length(sig);
    end
    A = EngeeDSP.Functions.fft(sig);
    B = EngeeDSP.Functions.fftshift(A);
    S = (2*B)/nsamples;
    out = 10log10.(abs.(S.^2));
    df = fs/nsamples;
        if onesided == true
            f = 0:df:fs/2;
            out = out[Int(ceil(nsamples/2)):end]
        else            
            f = -fs/2:df:fs/2-df;
        end
    return out, f
end

fftspectrum (generic function with 1 method)

Проанализируем область низких частот (от 0 до 1500 Гц). Найдём пики в спектре - они соответствуют гармоникам сигнала. В этом нам поможет функция findpeaks из набора функций EngeeDSP. Выделим первые шесть гармоник - это пики не ниже -50 дБ и с выраженностью не менее 30 - и отобразим их на графике:

spectrum, fvec = fftspectrum(sig, fs; nfft = nFFT, onesided = true);
pks, locs = EngeeDSP.Functions.findpeaks(spectrum, out=:data, 
                                                    MinPeakHeight = -50,
                                                    MinPeakProminence = 30);
plot(fvec, spectrum, linewidth=2, xlim=(0,1500),
        xguide = "Частота (Гц)", yguide = "Мощность (дБ)",
        title = "Гармоники на спектре аудиосигнала")
scatter!(fvec[locs], pks, legend = false)

Самый первый пик находится на частоте 219 Гц. Но мы также можем программно определить частоты первых шести гармоник и найти среднее расстояние между ними в Гц. Именно эту оценку мы и примем за основную частоту:

harmonics = fvec[locs[1:6]]

6-element Vector{Float32}:
  219.0
  441.0
  661.0
  881.0
 1101.0
 1321.0

Основную частоту вычислим статистически, как среднее арифметическое от разницы между частотами соседних пиков:

base_freq = EngeeDSP.Functions.mean(diff(harmonics))

220.4f0

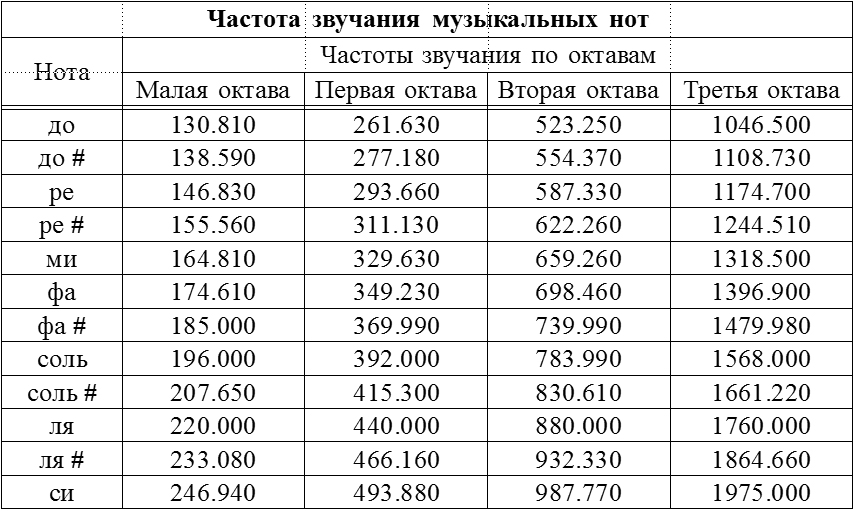
$chastoty_not.jpg$

Судя по таблице, сыгранная нота - это Ля малой октавы.

Заключение

Мы познакомились с функционалом EngeeDSP для задач вычисления быстрого преобразования Фурье и реализации алгоритма оценки спектра сигнала на его основе, решили практическую задачу определения характеристик аудиосигнала при помощи спектрального анализа.

БПФ и спектральный анализ с EngeeDSP

Функция FFT

Постановка задачи для анализа

Оценка спектра сигнала

Определение основной частоты

Заключение

Тип

Краткое описание

Связанные материалы

Теги

Категории

Языки

Форматы

Уровень

Статус

Опубликовано

Обновлено

Источник