Дуговая сталеплавильная печь
Моделирование дуговой сталеплавильной печи в статическом режиме
В этом примере рассмотрено моделирование в статическом режиме и анализ гармоник тока и напряжения для дуговой сталеплавильной печи ДСП-100НЗА ёмкостью 100 т и мощностью трансформатора 50 МВА.
Введение
Дуговая сталеплавильная печь (ДСП) является ключевым агрегатом современной металлургии, где высокотемпературная электрическая дуга, возникающая между электродами и металлической шихтой, служит основным источником энергии для переплава металлолома в высококачественную сталь. Широкое применение ДСП, особенно в производстве стали из лома, обусловлено их экономичностью и экологичностью, а перспективы технологии неразрывно связаны с дальнейшим повышением эффективности и снижением воздействия на энергосистему. Однако ДСП представляет собой чрезвычайно сложный для анализа и управления объект из-за ярко выраженной нелинейности, стохастичности дугового разряда и динамического изменения электрических параметров в ходе плавки. Именно эта сложность делает критически важным глубокое исследование адекватных схем замещения ДСП, которые являются основой для анализа режимов работы, проектирования и оптимизации систем управления. Разработка эффективных систем управления электродом необходима для стабилизации мощности дуги, минимизации фликкера и повышения энергоэффективности. Параллельно, тщательный анализ гармонического состава потребляемого тока и напряжения на шинах печи имеет первостепенное значение, так как ДСП – мощный источник высших гармоник, вызывающих искажение формы кривой напряжения в питающей сети, перегрузку оборудования и потенциальные проблемы электромагнитной совместимости. Исследование этих аспектов необходимо для обеспечения надежной работы самой печи, снижения потерь в сети и соблюдения нормативов качества электроэнергии.
Математическое описание
Существует несколько подходов к математическому описанию элементов электрической схемы замещения ДСП. Один из таких подходов, описывающий нелинейность сопротивления электрической дуги, приводится в [1]. Его мы и возьмём в качестве примера.
Приведённое в статье описание сопротивления дуги:
Представим в виде направленных блоков в подсистеме "Расчёт сопротивления дуги".
Модель Engee
Модель примера - electric_arc_furnace.engee.
Электрическая цепь включает в себя:
-
последовательные RL-цепочки кабельной линии, первичной и вторичной обмоток печного трансформатора,
-
датчик фазного напряжения для измерения напряжения на первичной обмотке,
-
датчик тока и напряжения для измерения тока и напряжения в фазах ДСП,
-
линейные переменные резисторы в каждой фазе для моделирования сопротивления дуги,
-
вспомогательные элементы: заземление нейтрали, нейтральный порт и разветвитель фаз.
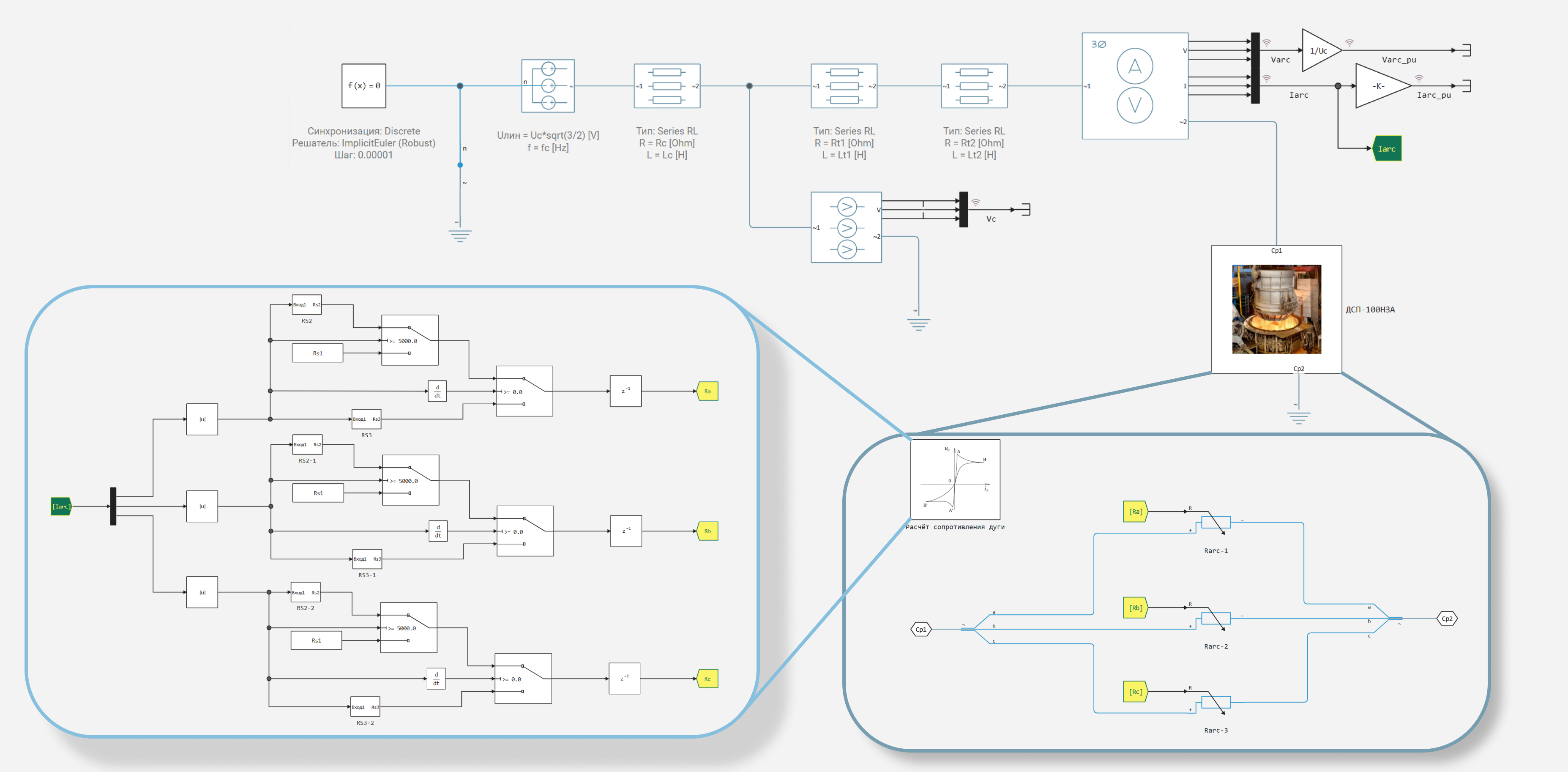
В модели записываются в переменную simout следующие сигналы:
-
Vc- трёхфазное напряжение на входе печного трансформатора [В], -
Varc- напряжение на каждой фазе ДСП [В], -
Varc_pu- относительное напряжение на каждой фазе ДСП [о.е.], -
Iarc- ток в каждой фазе ДСП [А], -
Iarc_pu- относительный ток в каждой фазе ДСП [о.е.],
Параметры модели также задаются согласно данным из публикации, их определение приведено ниэже:
Uc = sqrt(2)*573 # Амплитудное фазное напряжение сети (В)
fc = 50.0 # Частота сети (Гц)
Rc = 0.0528e-3; Xc = 0.468e-3; Lc = Xc/(2pi*50) # Параметры кабеля: R (Ом), X (Ом), L (Гн)
Rt1 = 0.05e-3; Xt1 = 0.35e-3; Lt1 = Xt1/(2pi*50) # Параметры трансформатора - первичная обмотка
Rt2 = 0.25e-3; Xt2 = 3.15e-3; Lt2 = Xt2/(2pi*50) # Параметры трансформатора - вторичная обмотка
println("Параметры системы: Rc = $Rc Ом, Lc = $Lc Гн")
println("Параметры Трансформатора ВН: Rt1 = $Rt1 Ом, Lt1 = $Lt1 Гн")
println("Параметры Трансформатора НН: Rt2 = $Rt2 Ом, Lt2 = $Lt2 Гн")
iзаж = 0.5e4; Imax = 1e5; # Ток зажигания и максимальный ток, А
uзаж = 310.5; uп = uзаж/1.15; # Напряжение зажигания и напряжение постоянной величины, В
uт = (Imax+iзаж)/Imax * uп; # Вспомогательный параметр
T1 = 1e-2; T2 = 2e-2; # Тепловые постоянные времени дуги, с
Rs1 = 25.87*1e-3; # Сопротивление дуги в зарядном прмежутке, Ом
Приведённые параметры также определяются в обратных вызовах модели.
Для выполнения моделирования получим путь к директории примера, перейдём в неё и подключим скрипт Julia для использования вспомогательных функций моделирования и анализа данных.
Прежде всего установим и подключим пакеты, необходимые для моделирования и анализа данных.
# Установка необходимых пакетов (если они ещё не установлены)
# JLD2 - для работы с файлами данных в формате HDF5/Julia
# FFTW - библиотека для быстрого преобразования Фурье (FFT)
# LinearAlgebra - стандартный модуль Julia для линейной алгебры
import Pkg; Pkg.add(["JLD2", "FFTW", "LinearAlgebra"])
# Подключение установленных пакетов
using JLD2, FFTW, LinearAlgebra
example_path = @__DIR__; # Получаем абсолютный путь к директории, содержащей текущий скрипт
cd(example_path); # Переходим в директорию примера
include("useful_functions.jl"); # Подключаем скрипт Julia со вспомогательными функциями
Моделирование
Получим данные моделирования - для этого можно выбрать "файл .jld2" для загрузки ранее записанных результатов моделирования или "модель .engee" для загрузки и запуска модели
# @markdown **Определите источник данных для анализа:**
источник = "модель .engee" # @param ["модель .engee","файл .jld2"]
simout = get_sim_results(источник, example_path)
Данные собраны, извлечём несколько интересующих нас переменных для анализа:
t = get_sim_data(simout, "Iarc_pu", 1, "time");
IarcA_pu = get_sim_data(simout, "Iarc_pu", 1, "value");
VarcA_pu = get_sim_data(simout, "Varc_pu", 1, "value");
IarcA = get_sim_data(simout, "Iarc", 1, "value");
VarcA = get_sim_data(simout, "Varc", 1, "value");
VcA = get_sim_data(simout, "Vc", 1, "value");
По полученным данным также определим конечное время моделирования, шаг модели и частоту расчёта модели.
T = last(t);
ST = T/(size(t)[1]-1);
fs = Int(round(1/ST));
Ток и напряжение
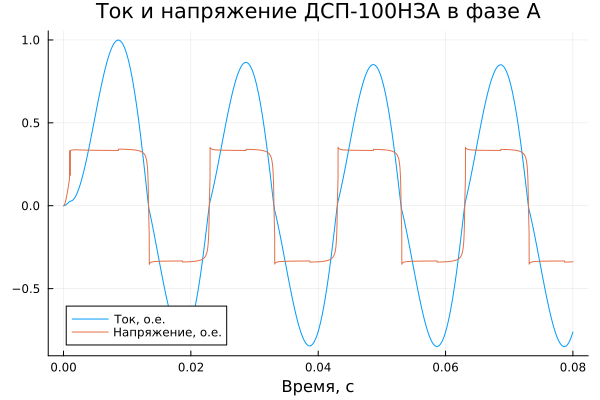
Выведем на графики осциллограммы относительных тока и напряжения на печной дуге для фазы А:
gr()
plot(t, [IarcA_pu, VarcA_pu];
label = ["Ток, о.е." "Напряжение, о.е."],
title = "Ток и напряжение ДСП-100НЗА в фазе А",
xlabel = "Время, с")
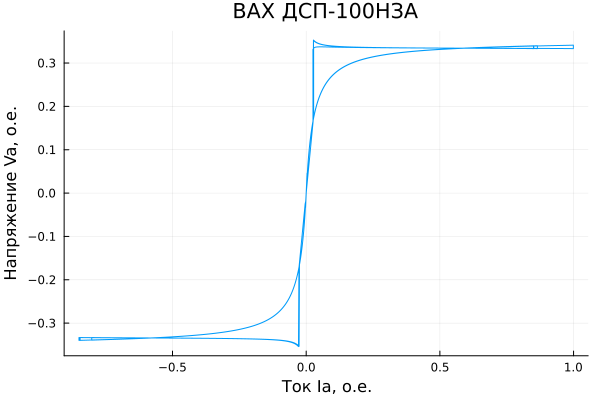
.Осциллограмму имеют ожидаемую форму, дополнительно можно представить эти два сигнала в виде вольт-амперной характеристики (ВАХ):
plot(IarcA_pu, VarcA_pu;
label = :none, title = "ВАХ ДСП-100НЗА",
xlabel = "Ток Ia, о.е.", ylabel = "Напряжение Va, о.е.")
ВАХ печной дуги также имеет ожидаемую форму. Следовательно, модель, построенная по описанию из публикации, корректна. Перейдём к анализу гармонических искажений тока и напряжения.
Гармонический анализ
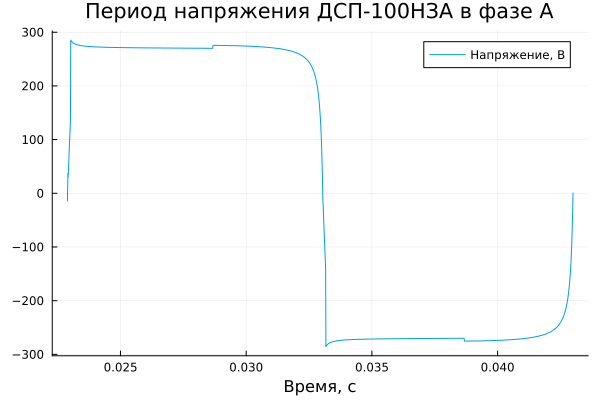
Для анализа гармоник в статическом режиме достаточно взять один период сигнала. Это будет сигнал напряжения печной дуги в фазе А на следующем интервале:
gr()
int = 2290:4301
plot(t[int], VarcA[int];
label = "Напряжение, В",
title = "Период напряжения ДСП-100НЗА в фазе А",
xlabel = "Время, с")
Получим вектора сигнала и времени для этого интервала:
signal = VarcA[int]; t = t[int];
При помощи функций из скрипта Julia получим данные об амплитудах и фазах гармонических составляющих заданного участка сигнала:
# Анализируем гармоники
results = analyze_harmonics(signal, fs, fc)
n, A, ph = get_harmonics_data(results)
# Выводим результаты
println("Гармоника | Амплитуда | Фаза (град)")
println("----------------------------------")
for (n, A, ph) in zip(n, A, ph)
round(A, digits=3)!=0.0 ? println(lpad(n, 9), " | ", lpad(round(A, digits=3), 9), " | ", round((ph)*180/pi, digits=3)) : nothing
end
При помощи следующей функции выделим данные об искажения отдельно для гармоник прямой, обратной и тройной последовательностей:
harm, harm2, harm3 = get_sequences(results, n);
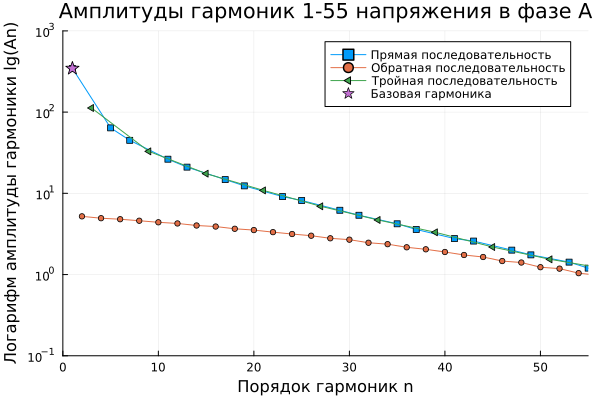
Амплитуды каждой из гармоник, выделенных в последовательности удобно также представить на графике в логарифмических осях:
gr()
plot( yaxis = :log, xlims=[0,55],ylims=[1e-1,1e3], title = "Амплитуды гармоник 1-55 напряжения в фазе А", xlabel="Порядок гармоник n", ylabel = "Логарифм амплитуды гармоники lg(An)")
plot!(harm[1], harm[2];
markershape = :square, markersize=3, label = "Прямая последовательность")
plot!(harm2[1], harm2[2];
markershape = :circle, markersize=3, label = "Обратная последовательность")
plot!(harm3[1], harm3[2];
markershape = :ltriangle, markersize=5, label = "Тройная последовательность")
scatter!([harm[1][1]], [harm[2][1]];
markershape = :star, markersize=7, label = "Базовая гармоника")
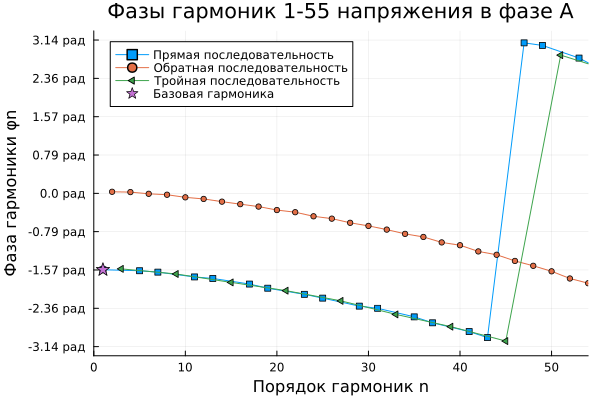
Аналогичный график можно представить и для фаз каждой из гармоник в последовательностях:
gr()
y = range(-π, π, length=9)
plot(xlims=[0,54], yticks = (y, ["$(round(yi, digits=2)) рад" for yi in y]), title = "Фазы гармоник 1-55 напряжения в фазе А", xlabel="Порядок гармоник n", ylabel = "Фаза гармоники φn")
plot!(harm[1], harm[3];
markershape = :square, markersize=3, label = "Прямая последовательность")
plot!(harm2[1], harm2[3];
markershape = :circle, markersize=3, label = "Обратная последовательность")
plot!(harm3[1], harm3[3];
markershape = :ltriangle, markersize=5, label = "Тройная последовательность")
scatter!([harm[1][1]], [harm[3][1]];
markershape = :star, markersize=7, label = "Базовая гармоника")
Уровни суммарных гармонических искажений
Суммарные уровни гармонических искажений, которые могут быть использованы для соотнесения с нормами качества электрической энергии согласно ГОСТ 32144-2013, определяются по формуле евклидовой нормы:
Рассчитаем уровни гармонических искажений напряжения - суммарный по всем гармоникам и по отдельным последовательностям.
THD_V = norm(vcat(harm[2][2:end], harm2[2], harm3[2]))/harm[2][1]*100;
THD_V0 = norm(harm[2][2:end])/harm[2][1]*100;
THD_V2 = norm(harm2[2])/harm[2][1]*100;
THD_V3 = norm(harm3[2])/harm[2][1]*100;
println("Суммарный коэффициент гармонических искажений напряжения: ", round(THD_V, digits=2), "%.\nИз него, по последовательностям:")
println("- прямая: ", round(THD_V0, digits=2), "%,")
println("- обратная: ", round(THD_V2, digits=2), "%,")
println("- тройная: ", round(THD_V3, digits=2), "%.")
Вычислим гармонические искажения для тока:
results_I = analyze_harmonics(IarcA, fs, fc);
n_I, A_I, ph_I = get_harmonics_data(results_I);
THD_I = norm(A_I[2:end])/A_I[1]*100
println("Суммарный коэффициент гармонических искажений тока: ", round(THD_I, digits=2), "%.")
Заключение
В этом проекте разработана статическая модель дуговой сталеплавильной печи ДСП-100НЗА, проведено моделирование, получены осциллограммы токов и напряжений, данные о гармоническом анализе. Полученные материалы лягут в основу дальнейших примеров, связанных с моделированием режимов, управлением ДСП а также повышением качества электроэнергии.
Литература
Черненко, А. Н. Динамическая модель печной дуги в Matlab (Simulink) / А. Н. Черненко, В. В. Вахнина, С. Г. Мартынова // Вектор науки Тольяттинского государственного университета. – 2015. – № 2-1(32-1). – С. 58-64. – EDN TYCPDV.