Неявнополюсный генератор без регуляторов
Неявнополюсный генератор без регуляторов
Описание модели
В этом примере рассматривается работа блока турбогенератор-трансформатор через двухцепную воздушную линию (ВЛ) на шину бесконечной мощности (ШБМ) без регуляторов возбуждения и скорости вращения. В момент времени 5 с. в модели происходит трёхфазное короткое замыкание (КЗ) в начале одной из цепей ВЛ. Проводится аналитический расчёт предельного времени отключения КЗ с помощью метода площадей и сравнение с результатами математического моделирования [1-3].
Показываются процесс запуска и настройки модели из среды разработки скрипта с помощью командного управления, обработка результатов моделирования, визуализация результатов моделирования и предложены сценарии для самостоятельной работы с моделью. Осуществляется логгирование сигналов, показаны их временные графики. Внешний вид модели:
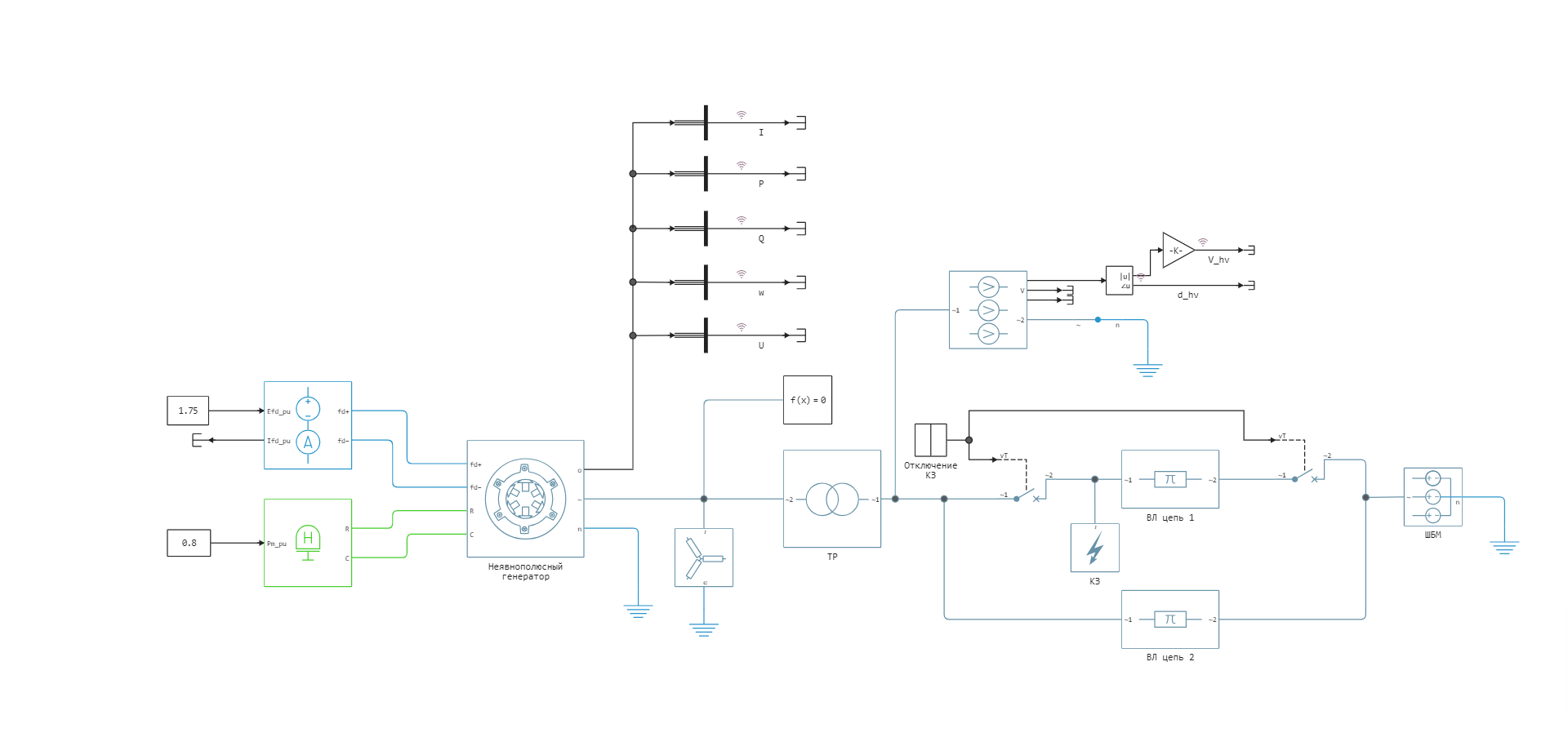
Основные блоки используемые в данном примере и их параметры:
- Synchronous Machine Round Rotor - неявнополюсный синхронный генератор (,).
- Voltage Source (Three-Phase) - трёхфазный источник напряжения, используется для моделирования ШБМ, установившийся режим выставлен с помощью задания действующего линейного напряжения и фазового сдвига (,).
- Fault (Three-Phase) - короткое замыкание.
- Из библиотеки пассивных элементов блоки трёхфазной ЛЭП Three-Phase PI Section Line (, АС 500/64, 2 цепи) и двухобмоточного трехфазного трансформатора Two-Winding Transformer (Three-Phase) (ТД-630000/500).
Расчёт предельного угла отключения методом площадей
Импортируем необходимые модули для работы с графиками:
using Plots;
gr();
Параметры ШБМ:
# номинальное напряжение, В
Us = 500e3
# мощность КЗ, ВА
Skz = 10e9
# полное сопротивление системы, Ом
Zkz = Us ^ 2 / Skz
# соотношение активного и индуктивного сопротивления
XR = 15
# индуктивное сопротивление системы, Ом
Xkz = Zkz * sin(atan(XR))
# активное сопротивление системы, Ом
Rkz = Zkz * cos(atan(XR))
# комплексное сопротивление системы, Ом
Zs = Rkz + 1im * Xkz;
Параметры ЛЭП:
# удельное сопротивление прямой последовательности, Ом/км
Z0 = 0.01967 + 0.2899im
# количество цепей
n = 2
# длина ВЛ, км
L = 200
# удельная емкостная проводимость, См/км
b0 = 3.908e-6
bc = b0 * L * n
# полное сопротивление ВЛ, Ом
Zl = Z0 * L / n
# емкостное сопротивление половины ВЛ, Ом
Zc = -2im / bc;
Параметры трансформатора:
# активное сопротивление ТР, Ом
Rt = 0.4514
# индуктивное сопротивление ТР, Ом
Xt = 30.62
Zt = Rt + Xt * 1im;
Параметры генератора:
# номинальное напряжение, В
Ug = 24e3
# номинальная мощность, ВА
Sg = 500e6
# активное сопротивление, о.е.
Ra = 0.003
# синхронное индуктивное сопротивление по оси d, о.е.
Xd = 1.81
# переходное индуктивное сопротивление по оси d, о.е.
Xdd = 0.3
# комплексное переходное сопротивление генератора, Ом
Zg = (Ra + Xdd * 1im) * Us ^ 2 / Sg;
Параметры нагрузки:
# активная мощность нагрузки, Вт
Pn = 20e6
# активное сопротивление нагрузки, Ом
Zn = Us ^ 2 / Pn;
Расчёт собственных и взаимных сопротивлений и в нормальном режиме методом единичного тока:
I2 = 1
Uc = I2 * Zs
Ic0 = Uc / Zc
Ibc = I2 + Ic0
Ub = Uc + Zl * Ibc
Ib0 = Ub / Zc
Iab = Ib0 + Ibc
Ua = Ub + Iab * Zt
Ia0 = Ua / Zn
I1 = Ia0 + Iab
U1 = Ua + I1 * (Xdd * 1im * Us ^ 2 / Sg)
Z12d = (Ua + I1 * (Xd * 1im * Us ^ 2 / Sg)) / I2
Z12 = U1 / I2
Z11 = U1 / I1
alpha11 = pi / 2 - angle(Z11)
alpha12 = pi / 2 - angle(Z12);
Расчёт собственных и взаимных сопротивлений и в послеаварийном режиме методом единичного тока:
I2 = 1
Uc = I2 * Zs
Ic0 = Uc / (2 * Zc)
Ibc = I2 + Ic0
Ub = Uc + 2 * Zl * Ibc
Ib0 = Ub / (2 * Zc)
Iab = Ib0 + Ibc
Ua = Ub + Iab * Zt
Ia0 = Ua / Zn
I1 = Ia0 + Iab
U1 = Ua + I1 * (Xdd * 1im * Us ^ 2 / Sg)
Z12_pav = U1 / I2
Z11_pav = U1 / I1
alpha11_pav = pi / 2 - angle(Z11_pav)
alpha12_pav = pi / 2 - angle(Z12_pav);
Расчёт угловых характеристик производится с использованием переходной ЭДС ,
которая остаётся неизменной в начальный момент времени КЗ и после его отключения:
# вырабатываемая генератором мощность в нормальном режиме
P0 = 400e6;
Q0 = 0;
# синхронная ЭДС по оси q
Eq = sqrt((Us + Q0 * abs(Z12d) / Us) ^ 2 + (P0 * abs(Z12d) / Us) ^ 2)
# угол ротора в исходном режиме
d0 = atan(P0 * abs(Z12d) / (Us ^ 2 + Q0 * abs(Z12d)))
# переходная ЭДС
Ep = sqrt((Us + Q0 * abs(Z12) / Us) ^ 2 + (P0 * abs(Z12) / Us) ^ 2)
# угол переходной ЭДС
d0p = atan(P0 * abs(Z12) / (Us ^ 2 + Q0 * abs(Z12)))
# переходная ЭДС по оси q в нормальном режиме
Eqq = Ep * cos(d0p - d0)
# переходная ЭДС по оси q в аварийном и послеаварийном режимах
Eqq_pav = Eqq
Eqq_av = Eqq
# максимальная активная мощность в нормальном режиме
Pmax = (Eqq ^ 2 / abs(Z11) * sin(alpha11) + Eqq * Us / abs(Z12)) / 1e6
# угол переходной ЭДС по оси q
d0p = asin(P0 / Pmax / 1e6)
# максимальная мощность в аварийном режиме
Pmax_av = 0
# максимальная мощность в послеаварийном режиме
Pmax_pav = (Eqq_pav ^ 2 / abs(Z11_pav) * sin(alpha11_pav) + Eqq_pav * Us / abs(Z12_pav)) / 1e6
# угол ротора при работе на послеаварийной характеристике
d0_pav = asin(P0 / Pmax_pav / 1e6)
# критический угол
dkr = pi - d0_pav
# предельный угол отключения
d_pr = acos((P0 * 1e-6 * (pi - d0_pav - d0p) + Pmax_pav * cos(pi - d0_pav) - Pmax_av * cos(d0p)) / (Pmax_pav - Pmax_av));
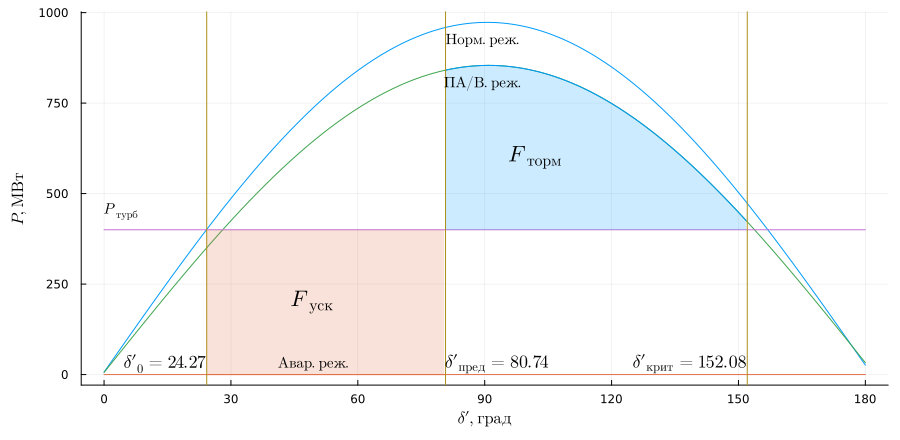
Визуализация метода площадей:
# функции угловых характеристик
delta = 0:0.1:180
Pmax = x -> (Eqq ^ 2 / abs(Z11) * sin(alpha11) .+ (Eqq * Us / abs(Z12)) * sin.(x .- alpha12)) / 1e6
Pmax_av = x -> fill(0, size(x))
Pmax_pav = x -> (Eqq_pav ^ 2 / abs(Z11_pav) * sin(alpha11_pav) .+ Eqq_pav * Us / abs(Z12_pav) * sin.(x .- alpha12_pav)) / 1e6
Pt = x -> fill(P0 * 1e-6, size(x))
# визуализация метода площадей
plot(delta, [Pmax(delta .* pi ./ 180) Pmax_av(delta .* pi ./ 180) Pmax_pav(delta .* pi ./ 180) Pt(delta)],
label = [L"Норм.реж." L"Авар.реж." L"П/АВ.реж." L"Мощн.турбины"], ylabel = L"P, МВт", xlabel = L"\delta\prime, град", legend=false,
xaxis = (0:30:180), size = (900,440), left_margin=5Plots.mm, bottom_margin=5Plots.mm)
plot!((d0p:0.01:d_pr) .* 180 / pi, Pmax_av((d0p:0.01:d_pr)), fillrange = Pt((d0p:0.01:d_pr)), fillalpha = 0.2, c = 2, label = "Fторм")
plot!((d_pr:0.01:dkr) .* 180 / pi, Pmax_pav((d_pr:0.01:dkr)), fillrange = Pt((d_pr:0.01:dkr)), fillalpha = 0.2, c = 1, label = "Fторм")
vline!([d0p,d_pr,dkr] .* 180 / pi, c = 5)
annotate!([(90, Pmax(pi / 2) - 50, (L"Норм.реж.", 10, :black)),
(50, Pmax_av(pi / 2) .+ 30, (L"Авар.реж.", 10, :black)),
(90, Pmax_pav(pi / 2) - 50, (L"ПА/В.реж.", 10, :black)),
(d0p * 180 / pi + 20, P0 * 1e-6 - 200, (L"F_{уск}", 15, :black, :left)),
(d_pr * 180 / pi + 15, P0 * 1e-6 + 200, (L"F_{торм}", 15, :black, :left)),
(0, P0 * 1e-6 + 50, (L"P_{турб}", 10, :black, :left)),
(d0p * 180 / pi, 30, (L"\delta\prime_0 = %$(round(d0p * 180 / pi, digits=2))", 12, :black, :right)),
(d_pr * 180 / pi, 30, (L"\delta\prime_{пред} = %$(round(d_pr * 180 / pi, digits=2))", 12, :black, :left)),
(dkr * 180 / pi, 30, (L"\delta\prime_{крит} = %$(round(dkr * 180 / pi, digits=2))", 12, :black, :right))])
Предельное время отключения КЗ:
Tj = 7.05
tpr = sqrt((d_pr - d0p) * 2 * Tj / (0.8 * 2 * pi * 50))
print("t_пред = $(round(tpr, digits = 3))")
Моделирование
Загрузка модели:
model_name = "synchronous_generator_round_rotor";
model_name in [m.name for m in engee.get_all_models()] ? engee.open(model_name) : engee.load( "$(@__DIR__)/$(model_name).engee");
Настройка модели с помощью командного управления на время отключения линии и КЗ равным 0,24 c, при котором динамическая устойчивость сохранится:
step = "Отключение КЗ";
# отключение цепи ВЛ
engee.set_param!(model_name * "/" * step, "Time" => 5.24);
Запуск загруженной модели:
results = engee.run(model_name);
Для импорта результатов моделирования было заранее включено логгирование необходимых сигналов и заданы их имена. Преобразуем результаты моделирования из переменной results:
# вектор времени симуляции
sim_time = results["w"].time;
# вектор скорости вращения ротора
w1 = results["w"].value;
# вектор тока генератора
P1 = results["P"].value;
Моделирование при увеличении длительности КЗ до 0,2402 с:
# отключение цепи ВЛ
engee.set_param!(model_name*"/"*step, "Time" => 5.2402);
results = engee.run(model_name);
# вектор скорости вращения ротора
w2 = results["w"].value;
# вектор тока генератора
P2 = results["P"].value;
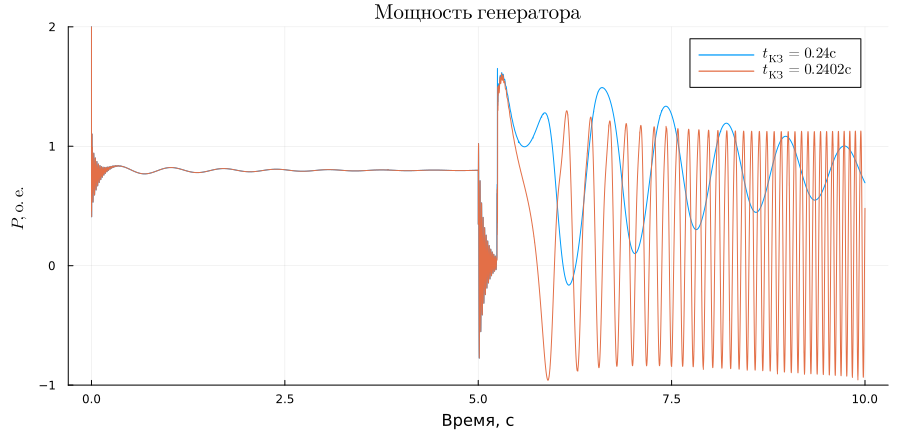
Графики активной мощности генератора:
plot(sim_time, P1, title = L"Мощность\; генератора", ylabel = L"P, о.е.", xlabel="Время, c", label = L"t_{КЗ} = 0.24 с", legendfontsize = 10)
plot!(sim_time, P2, label = L"t_{КЗ} = 0.2402 с", ylims = (-1, 2),size = (900,440), left_margin=5Plots.mm, bottom_margin=5Plots.mm)
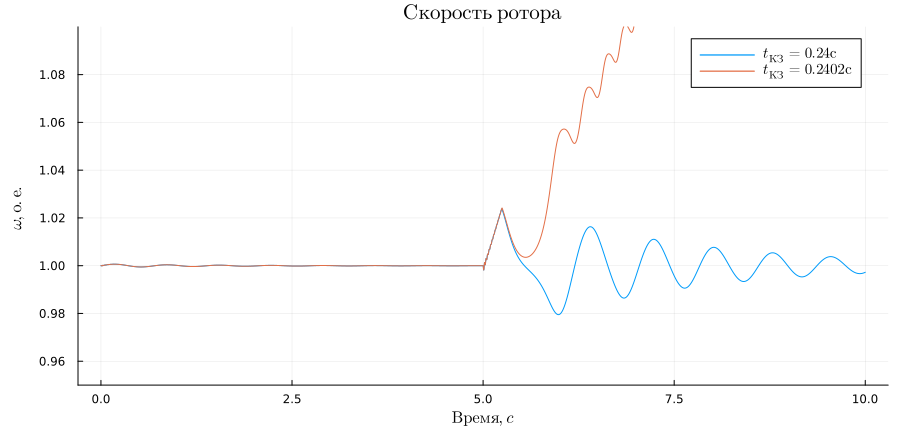
Графики скорости ротора:
plot(sim_time, w1, title = L"Скорость\; ротора", ylabel = L"\omega, о.е.", xlabel=L"Время, c", label = L"t_{КЗ} = 0.24 с", legendfontsize = 10)
plot!(sim_time, w2, label = L"t_{КЗ} = 0.2402 с", ylims = (0.95, 1.1),size = (900,440), left_margin=5Plots.mm, bottom_margin=5Plots.mm)
Во втором опыте динамическая устойчивость генератора нарушилась, таким образом было эмперически найдено предельное время отключения КЗ в модели. Результат с небольшой погрешностью сходится с теоретическим расчётом.
println("Предельное время отключения аналитически = "*string(round(tpr, digits=3)) * "с")
println("Предельное время отключения практически = "*string(0.24) * "с")
Дополнение
Попробуйте самостоятельно изменить следующие параметры модели и исследовать, как это влияет на динамическую устойчивость:
- увеличить длину ВЛ на 200 км;
- вид КЗ в блоке Fault (Three-Phase);
- снизить активную мощность генератора в исходном режиме на 200 МВт.
Выводы
В данном примере были использованы инструменты для командного управления моделью Engee и выгрузки результатов моделирования, показана работа с модулем Plots. Была рассмотрена работа неявнополюсного генератора через трансформатор и двухцепную ВЛ на ШБМ без регуляторов возбуждения и скорости вращения. Проведен аналитический расчёт динамической устойчивости и выполнено сравнение результатов с данными моделирования.
Ссылки
- Веников В. А. Переходные электромеханические процессы в электрических системах: Учеб. для электроэнергет. спец. вузов. — 4-е изд., перераб. и доп. — М.: Высш. шк., 1985
- Переходные процессы электрических систем в примерах и иллюстрациях: Учебное пособие для вузов (В. В. Ежков, Н. И. Зеленохат, И. В. Литкенс и др.; Под ред. В. А. Строева). - М.: Знак, 1996. - 224с., ил.
- Долгов А.П. Устойчивость электрических систем : учебное пособие / Долгов А.П.. — Новосибирск : Новосибирский государственный технический университет, 2010. — 177 c. — ISBN 978-5-7782-1320-3.