Mass on an inclined plane

Let's implement a simple model from physics and mechanics courses and see if it is easy to calculate the behavior of this system in the Engee physical modeling environment.

Description of the model

Let's consider a simple problem about a load of a given mass that slides over a surface with known friction parameters.

The calculation of such tasks is usually done for pedagogical purposes. The problem is very well formulated, it is very easy to translate into reality (* unlike even flip blocks with coils*), and its solution shows the ability to combine and manipulate useful abstractions of physics and mathematics.

The solution of such a problem in the 1D modeling package requires some reservations. For the first purpose, these packages * do not consider the relative movement of objects*, so we will not see an inclined surface and will not be able to tilt it to conduct a physical simulation.

The Engee physical modeling blocks are designed to calculate the dynamics of a single presented situation, and our task fits perfectly into this statement.

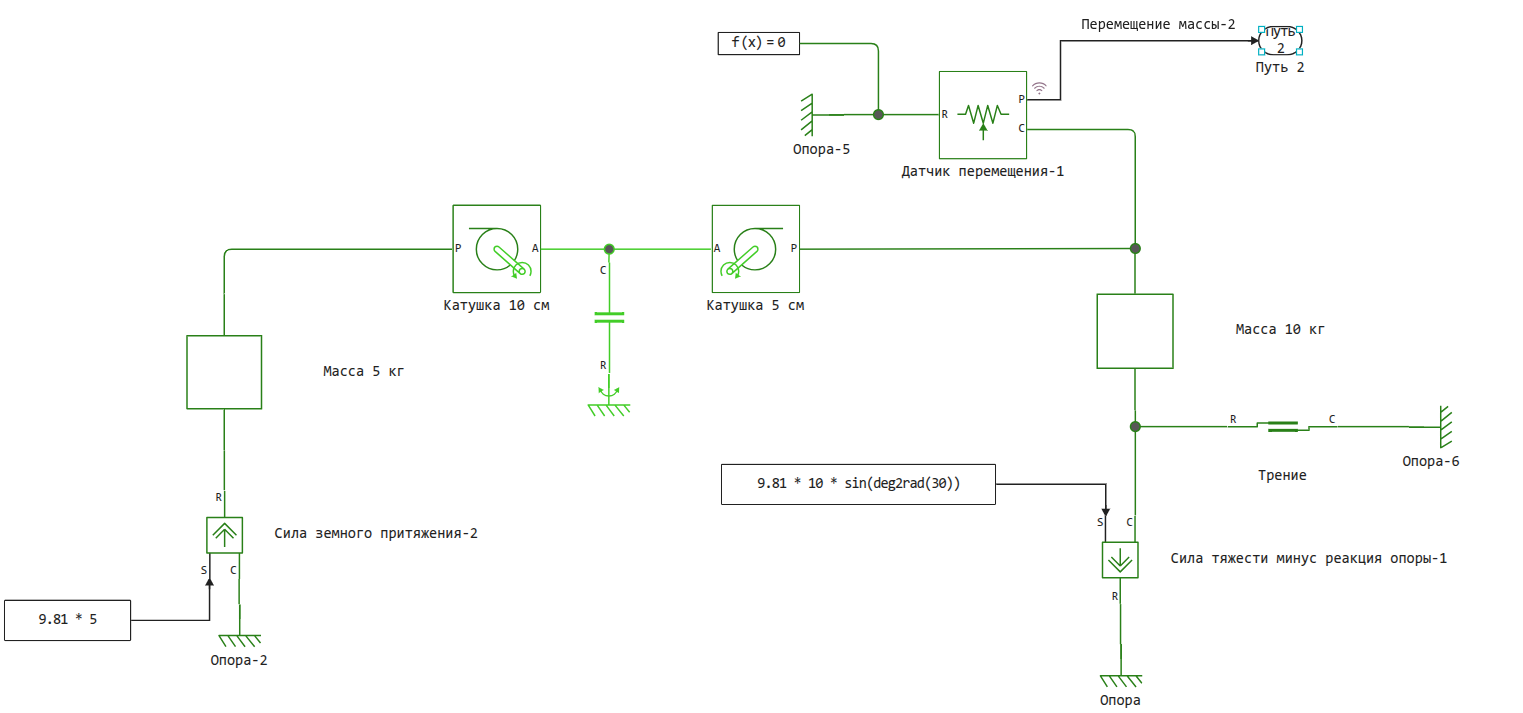
Let's consider the scheme of this system from the point of view of cargo:

On the cargo (Масса) only ** gravity** acts (acceleration 9.81 multiplied by mass minus the component of gravity that is compensated by the reaction of the support) and ** friction** (its direction does not play a big role, although the tilt of the bench may affect the parameters).

The load * "does not know"* at what angle the bench is tilted. But he feels a certain combination of forces, which are expressed in a change in his condition. The movement of the load is detected by a sensor and measured relative to a certain support.

An important note. Friction is calculated in proportion to the reaction force of the support (). This expression should be written in the block Трение in the parameter Dry friction, when changing the tilt of the bench, you will need to enter the block Трение and update the value.

A more complex experiment

What if we want to add a few more interactions to this model? The model remains clear and will be understandable to a wide variety of specialists even without reading the accompanying description.

We've added another one to the model. Массу 5 кг which is hanging on a rope wound on Катушку 10 см (diameter), which is rigidly connected to the other Катушкой 5 см (there is friction in their axis) and prevents slipping Массы 10 кг down the bench.

Calculating the model

There are many ways to launch this model. One of them is to open it on canvas Engee and click on the start button and study graphics panel graphs .

Another option is to run the model from a script and get the data for further analysis.:

model = engee.open("Масса на наклонной плоскости.engee");
data = engee.run(model)

SimulationResult(
    "Перемещение массы" => WorkspaceArray{Float64}("Масса на наклонной плоскости/Перемещение массы")
,
    "Перемещение массы-2" => WorkspaceArray{Float64}("Масса на наклонной плоскости/Перемещение массы-2")

)

In the structure data it contains several tables, one of which corresponds to a variable x, where the path traveled by a body of some mass over a surface with a given friction under the influence of gravity is preserved.

experiment_1 = collect(data["Перемещение массы"]);
experiment_2 = collect(data["Перемещение массы-2"]);

Let's print a graph.

plot(experiment_1.time, experiment_1.value, title="Перемещение массы по наклонной скамье", label="Без противовеса", titlefont=font(11), markershape=:o)
plot!(experiment_2.time, experiment_2.value, label="С противовесом", markershape=:o)

As we can see, the counterweight pulls the mass up the bench, and in the sensor coordinate system it performs a negative displacement (the path cannot be negative).

Conclusion

It is very likely that the classical problems from the physics textbook cannot be simplified even more, only to complicate the description in favor of an automated solution. But in serious engineering projects, it is usually not a universal physical modeling environment that is needed, but a well-understood description of a specific phenomenon, abstracted from unnecessary interactions.

1D modeling provides a fairly convenient formalism for calculating physical problems. Here you can use force or displacement sensors to solve simple basic tasks, and the graphical nature of the models allows you to combine them into subsystems or simply assemble fairly complex and visual computational experiments.