Engee documentation
Notebook

Designing a smartphone camera focus SAU

Let's connect the necessary libraries.

In [ ]: 
import Pkg; 
Pkg.add(["ControlSystemIdentification", "ControlSystems"])
In [ ]: 
using ControlSystems                # основная библиотека для работы с САУ
using ControlSystemIdentification   # библиотека для оценки динамических моделей на основе данных

Control object

The model below simulates the autofocus control system of a smartphone camera.

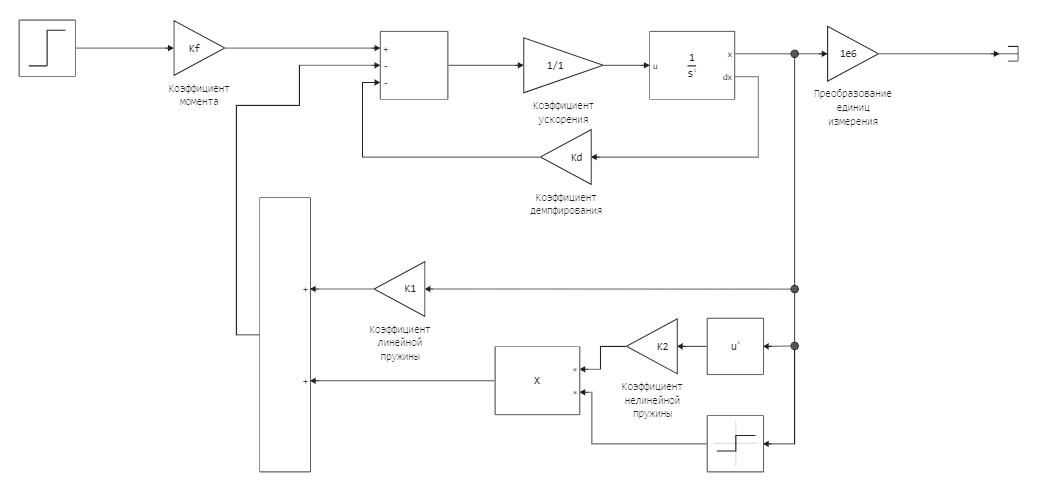
image.png

Consider the smartphone autofocus model. The smartphone electronics control the motor by feedback from the camera. Let's abstract from the technology and say that we need the transient process to take no more than 0.6 seconds from the moment of receiving the command to focus. Let's try to realise such a system using a PID controller.

Our motor-lens system is nonlinear, so first of all we linearise the model.

Linearisation of the control object

Let's run the model using command control. As a result, in the workspace we get the variable data, which contains the simulation results.

In [ ]: 
modelName = "Линза_ОУ"
if !(modelName in [m.name for m in engee.get_all_models()]) engee.load( "$(@__DIR__)/$(modelName).engee"); end;
data = engee.run( modelName )
Out[0]:
SimulationResult(
    "Преобразование единиц измерения.1" => WorkspaceArray{Float64}("Линза_ОУ/Преобразование единиц измерения.1")
,
    "Ступенчатая функция.1" => WorkspaceArray{Float64}("Линза_ОУ/Ступенчатая функция.1")

)

Let's write the data of input and output signals in variables and plot them on the graph.

In [ ]: 
dataIn = collect(data["Ступенчатая функция.1"]).value;
dataOut = collect(data["Преобразование единиц измерения.1"]).value;
data_t = collect(data["Преобразование единиц измерения.1"]).time;

plot( data_t, [dataIn dataOut], label=["Входной сигнал" "Выходной сигнал"] )
Out[0]:

Let's proceed to linearisation of the model. All methods for model identification of the library ControlSystemIdentification take as input an object of AbstractIdData type. To get the object of identification data of the time domain allows the function iddata. Then, using the method subspaceid we obtain a description of the system in the form of state space.

In [ ]: 
Ts = data_t[2] - data_t[1]                     # Получим частоту дискретизации системы из вектора времени
d  = iddata(dataOut, dataIn, Ts);              # создаем объект идентификации данных во временном пространстве 
sys_d = subspaceid(d, :auto);                  # запускаем метод идентификации модели пространства состояний

Let's compare the obtained description of the model with the model collected in the modelling environment. For this purpose we will use the block Пространство состояний and write there the obtained values A,B,C,D as matrix values.

In [ ]: 
sys = d2c(sys_d);   # перейдем к непрерывной модели
A = sys.A;          # находим матрицу A
B = sys.B;          # находим матрицу B
C = sys.C;          # находим матрицу C
D = sys.D;          # находим матрицу D

┌ Warning: d2c does not handle a non-zero cross covariance S, S will be set to zero
└ @ ControlSystemIdentification /usr/local/ijulia-demos/packages/ControlSystemIdentification/KM4Nc/src/ControlSystemIdentification.jl:359

Selection of coefficients: function pid()

To evaluate the suitability of the selected coefficient values, we will plot the LFCC, LFCC and Nyquist hodograph. We will also evaluate the quality of the transient process. For convenient display of frequency response plots, the function pid_marginplot is implemented below. It substitutes the values of the obtained system at the board into the functions for plotting frequency characteristics: marginplot and nyquistplot, and displays them on the graphs.

In [ ]: 
function pid_marginplot(C)
    f1 = marginplot(sys_tf * C, w)
    f2 = nyquistplot(sys_tf * C, xlims=(-10,1), ylims=(-2, 10), title="")
    plot(f1,f2, titlefontsize=10)
end
Out[0]:
pid_marginplot (generic function with 1 method)

Let us set additional variables. Transform the representation of the system into the form of a transfer function and set the frequencies for which we will build time and frequency characteristics.

In [ ]: 
sys_tf = tf(sys);
w = exp10.(LinRange(-2.5, 3, 500));

We will set the coefficients using the cell mask. By moving the sliders, you set a new value of the variable. If you change one coefficient, the code under the mask is recalculated. If you want to change several parameters at once, switch off auto refresh under the cell start button and start the cell manually.

The selection of coefficients is iterative, so first we will evaluate the characteristics of the system without the regulator, then we will start changing each one and evaluate the impact of changes on the system.

In [ ]: 
kp = 0.4 # @param {type:"slider", min:0.1, max:5, step:0.1}
ki = 1.322 # @param {type:"slider", min:0.0, max:20, step:0.001}
kd = 0.03 # @param {type:"slider", min:0.0, max:0.5, step:0.01}
Tf = 0.012 # @param {type:"slider", min:0.0, max:1, step:0.001}

C0 = pid(kp, ki, kd; Tf, form=:parallel, filter_order=2)
pid_marginplot(C0)
Out[0]:

Let's check whether our system is stable. This can be done by the function isstable.

In [ ]: 
isstable(feedback(sys_tf * C0))     # Проверка: устойчива ли система с полученным ПИД регулятором
Out[0]:
true

Then, if the system is stable and the stability margin satisfies our requirements, we construct a transient process and evaluate the quality of its characteristics.

In [ ]: 
plot(stepinfo(step(feedback(sys_tf * C0), 5)))      # Оценка переходного процесса САУ
Out[0]:

The obtained controller data can be used for the model in the simulation environment. For this purpose, we can take the values of coefficients from the working region and specify them in the PID regulator block.

Coefficient selection: function loopshapingPID()

Coefficient selection using the loopshapingPID function is based on the Loop Shaping approach, which allows you to specify the desired shape of the open loop frequency response to provide the desired closed loop characteristics. Thus, this method is convenient if the desired frequency properties of the system are known (e.g. desired bandwidth or disturbance suppression level).

Let us try to apply this method to our example and obtain the desired characteristics.

The function takes the description of the system in the form of a transfer function and the frequency at which it is desirable to achieve the unity gain of the open loop system. Additionally, the function accepts the parameter values of the additional sensitivity function Mt and the desired phase shift ϕt. By default, these parameters have optimal values, but they can be changed. It is also possible to adjust the shape of the synthesised PID controller and display graphs that will help to evaluate the quality of the obtained control system.

In [ ]: 
ω  = 17
Tf = 1/1000ω   
C0, kp, ki, kd, fig, CF = loopshapingPID(sys_tf, ω; Mt = 1.3, ϕt = 75, form=:parallel, doplot = true)
Out[0]:
(C = TransferFunction{Continuous, ControlSystemsBase.SisoRational{Float64}}
0.0493284587237057s^2 + 1.0063456913621145s + 6.26737143322893
--------------------------------------------------------------
                             1.0s

Continuous-time transfer function model, kp = 1.0063456913621145, ki = 6.26737143322893, kd = 0.0493284587237057, fig = Plot{Plots.PlotlyJSBackend() n=18}, CF = TransferFunction{Continuous, ControlSystemsBase.SisoRational{Float64}}
0.0493284587237057s^2 + 1.0063456913621145s + 6.26737143322893
--------------------------------------------------------------
   3.4602076124567474e-9s^3 + 8.31890330807703e-5s^2 + 1.0s

Continuous-time transfer function model)

Let's try to change the frequency. If we analyse the Nyquist diagram, we can notice that the characteristic passes very close to the critical point. Let's try to correct this and set ω = 17. Now the characteristic of the corrected system will touch the circle Mt at the point where ω = 17 at an angle ϕt = 75.

In [ ]: 
plot(fig)
Out[0]:

Let us verify the stability of the obtained system.

In [ ]: 
isstable(feedback(CF*sys_tf))
Out[0]:
true

Let us plot the LFC and LFCC of the system and reflect the stability reserves.

In [ ]: 
marginplot([sys_tf, CF*sys_tf])
Out[0]:

We also construct the transient process of the obtained ACS. We see that the transient time is about 0.4 s, which satisfies our requirements.

In [ ]: 
plot(stepinfo(step(feedback(CF * sys_tf), 1)))
Out[0]:

Using the obtained PID regulator we simulate the system in the simulation environment. And plot the results on the graph.

Blocks used in example