filter

Одномерный цифровой фильтр.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

y = filter(b, a, x) — фильтрует входные данные x, используя рациональную передаточную функцию, определяемую коэффициентами числителя и знаменателя b и a.

Подробнее про рациональную передаточную функцию см. Рациональная передаточная функция.

Если a(1) не равно 1, то функция filter нормирует коэффициенты фильтра по a(1). Следовательно, a(1) должно быть отличным от нуля.
- Если x — вектор, то filter возвращает отфильтрованные данные в виде вектора того же размера, что и x.
- Если x — матрица, то filter действует по первому измерению и возвращает отфильтрованные данные для каждого столбца.
- Если x — многомерный массив, то filter действует по первому измерению массива, размер которого не равен 1.

y = filter(b, a, x, zi) — использует начальные условия zi для задержек фильтра. Длина zi должна быть равна max(length(a),length(b))-1.

y = filter(b, a, x, zi, dim) — действует по размерности dim. Например, если x является матрицей, то filter(b, a, x, zi, 2) возвращает отфильтрованные данные для каждой строки.

y, zf = filter(___; out=2) — также возвращает конечные условия zf для задержек фильтра, используя любой из предыдущих синтаксисов. Если указано out=1, то filter возвращает один выходной аргумент.

Аргументы

Входные аргументы

# b — коэффициенты числителя передаточной функции
скаляр| вектор |матрица

Details

Коэффициенты числителя передаточной функции, заданные в виде скаляра, вектора или матрицы.

Подробнее про рациональную передаточную функцию см. Рациональная передаточная функция.

Типы данных	`Float64`, `Float32`, `Int8`, `Int16`, `Int32`, `Int64`, `UInt8`, `UInt16`, `UInt32`, `UInt64`
Поддержка комплексных чисел	Да

# a — коэффициенты знаменателя передаточной функции
скаляр| вектор |матрица

Details

Коэффициенты знаменателя передаточной функции, заданные в виде скаляра, вектора или матрицы.

Подробнее про рациональную передаточную функцию см. Рациональная передаточная функция.

Типы данных	`Float64`, `Float32`, `Int8`, `Int16`, `Int32`, `Int64`, `UInt8`, `UInt16`, `UInt32`, `UInt64`
Поддержка комплексных чисел	Да

# x — входные данные
вектор | матрица | N-мерный массив

Details

Входные данные, заданные в виде вектора, матрицы или N-мерного массива.

Типы данных	`Float64`, `Float32`, `Int8`, `Int16`, `Int32`, `Int64`, `UInt8`, `UInt16`, `UInt32`, `UInt64`
Поддержка комплексных чисел	Да

# zi — начальные условия для задержек фильтра
[] (по умолчанию) | вектор | матрица | N-мерный массив

Details

Начальные условия для задержек фильтра, заданные в виде вектора, матрицы или N-мерного массива:

Если zi — вектор, то его длина должна быть равна max(length(a),length(b))-1.
Если zi — матрица или N-мерный массив, то размер начального измерения должен быть равен max(length(a),length(b))-1. Размер каждого оставшегося измерения должен соответствовать размеру соответствующего измерения из x. Например, рассмотрим возможность использования filter во втором измерении (dim = 2) массива x размерностью 3 на 4 на 5. Массив zi должен иметь размер [max(length(a),length(b))-1] на 3 на 5.

Значение по умолчанию, указанное как [], инициализирует все задержки фильтра до нуля.

Типы данных	`Float64`, `Float32`, `Int8`, `Int16`, `Int32`, `Int64`, `UInt8`, `UInt16`, `UInt32`, `UInt64`
Поддержка комплексных чисел	Да

# dim — измерение для выполнения фильтрации
скаляр

Details

Измерение для выполнения фильтрации, заданное как целый положительный скаляр. Если измерение не указано, то по умолчанию будет использоваться первое измерение массива, размер которого не равен 1.

Рассмотрим двумерный входной массив x.

Если dim = 1, то filter(b, a, x, zi, 1) работает со столбцами x и возвращает фильтр, примененный к каждому столбцу.
Если dim = 2, то filter(b,a,x,zi,2) работает по строкам x и возвращает фильтр, примененный к каждой строке.

Если dim больше, чем ndims(x), тогда filter рассматривает x как будто у него есть дополнительные измерения вплоть до dim с размерами 1. Например, если x — матрица 2 на 3, a dim = 3, то filter работает в третьем измерении x как будто он имеет размер 2 на 3 на 1.

Типы данных

Float64, Float32, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64

Выходные аргументы

# y — отфильтрованные данные
вектор | матрица | N-мерный массив

Details

Отфильтрованные данные, возвращаемые в виде вектора, матрицы или N-мерного массива того же размера, что и входные данные x.

Если x имеет тип Float32, то filter изначально выполняет вычисления с одинарной точностью, и y также имеет тип Float32. В противном случае, y возвращается как тип Float64.

Типы данных

Float64, Float32

# zf — конечные условия для задержек фильтра
вектор | матрица | N-мерный массив

Details

Конечные условия для задержек фильтра, возвращаемые в виде вектора, матрицы или N-мерного массива.

Если x — вектор, то zf — вектор-столбец длины max(length(a),length(b))-1.
Если x — матрица или N-мерный массив, то zf — массив векторов-столбцов такой длины max(length(a),length(b))-1, что количество столбцов в zf эквивалентно количеству столбцов в x. Например, рассмотрим возможность использования filter во втором измерении (dim = 2) массива x размером 3 на 4 на 5. Массив zf будет иметь размер [max(length(a),length(b))-1] на 3 на 5.

Типы данных

Float64, Float32

Примеры

Фильтр скользящего среднего

Details

Фильтр скользящего среднего — распространенный метод сглаживания зашумленных данных. В этом примере функция фильтра используется для вычисления средних значений по вектору данных.

Создаем вектор-строку размером 1 на 100 синусоидальных данных, искаженных случайным шумом.

import EngeeDSP.Functions: filter
using Random
Random.seed!(0)
t = range(-pi, pi, length=100)
x = sin.(t) + 0.25 * randn(length(t))

Скользящий средний фильтр перемещает окно длиной windowSize вдоль данных, вычисляя среднее значение данных, содержащихся в каждом окне. Следующее разностное уравнение определяет фильтр скользящего среднего для вектора :

Для окна размером 5 вычислим коэффициенты числителя и знаменателя для рациональной передаточной функции.

windowSize = 5
b = (1/windowSize) * ones(windowSize)
a = [1.0]

Найдем скользящее среднее значение данных и сопоставим его с исходными данными.

y = filter(b, a, x)

plot(t, x,
     label="Input Data",
     linewidth=1.5,
     grid=true)

plot!(t, y,
      label="Filtered Data",
      linewidth=2,
      color=:red)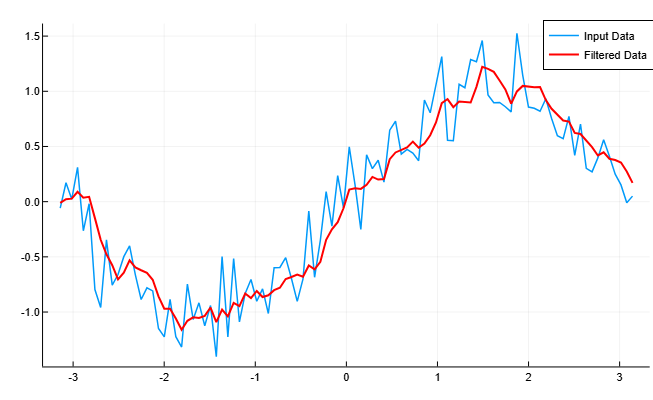

filter 4

Дополнительно

Рациональная передаточная функция

Details

Описание входов и выходов выполнения функции filter для вектора в области Z-преобразования представляет собой рациональную передаточную функцию. Рациональная передаточная функция имеет вид:

Рациональная передаточная функция применима как к фильтрам с конечной импульсной характеристикой (КИХ), так и к фильтрам с бесконечной импульсной характеристикой (БИХ) [1]. Здесь — Z-преобразование входного сигнала x, — Z-преобразование выходного сигнала , — порядок фильтра обратной связи, а — порядок фильтра прямой связи. В связи с нормировкой, предположим, что .

Для дискретного сигнала с элементами можно выразить рациональную передаточную функцию в виде разностного уравнения:

Кроме того, можно представить рациональную передаточную функцию, используя ее транспонированную реализацию в прямой форме II, как показано на диаграмме цифрового БИХ-фильтра. На диаграмме . Если порядки фильтров обратной и прямой связи не равны , то члены более высокого порядка можно считать равными 0. Например, для фильтра с a = [1, 2] и b = [2, 3, 2, 4] можно принять a = [1, 2, 0, 0].

filter 3

Выполнение фильтра filter в точке отсчета определяется разностными уравнениями для временной области:

По умолчанию функция filter инициализирует задержки фильтра равными нулю, . При этой инициализации предполагается, что как прошлые входные данные, так и выходные данные равны нулю. Чтобы включить ненулевые прошлые входные данные в текущие данные, укажите начальные условия для текущих данных в качестве задержек фильтра. Задержки фильтра можно рассматривать как конечные условия, которые получаются в результате применения одной и той же передаточной функции к предыдущим входам (и предыдущим выходам). Можно указать четвертый входной аргумент zi при использовании filter для установки задержек фильтра, zi(k). Также можно указать второй выходной аргумент zf при использовании filter для доступа к конечным условиям, zf(k).

Литература

Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999.