diric

Функция Дирихле или периодическая функция кардинального синуса.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

y = diric(x, n) — возвращает значения функции Дирихле степени n, вычисленные для элементов входного массива x.

Аргументы

Входные аргументы

# x — входные данные
скаляр | вектор | матрица

Details

Входные данные, заданные в виде вещественного скаляра, вектора или матрицы. Если x не скаляр, то diric применяется к каждому элементу.

Типы данных

Float32, Float64

# n — степень функции
скаляр

Details

Степень функции, заданная в виде положительного целого скаляра.

Типы данных

Float32, Float64

Выходные аргументы

# y — выходные данные
скаляр | вектор | матрица

Details

Выходные данные, возвращаемые в виде вещественного скаляра, вектора или матрицы той же размерности, что и x.

Типы данных

Float32, Float64

Примеры

Функция Дирихле

Details

Вычислим и построим график функции Дирихле между и для и . Функция имеет период для нечетных и для четных .

import EngeeDSP.Functions: diric

x = range(-2π, 2π, length=301)

d7 = diric.(x, 7)
d8 = diric.(x, 8)

plot(layout = (2, 1))

plot!(x/π, d7, subplot = 1)
ylabel!("N = 7", subplot = 1)
title!("Dirichlet Function", subplot = 1)

plot!(x/π, d8, subplot = 2)
ylabel!("N = 8", subplot = 2)
xlabel!("x / π", subplot = 2)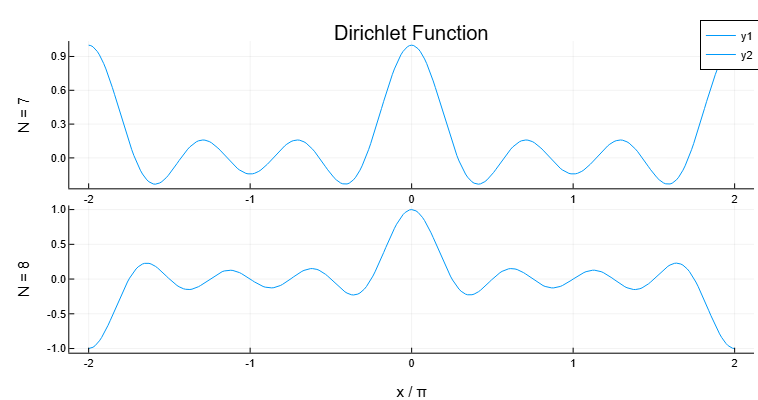

diric 1

Дополнительно

Функция Дирихле

Details

Функция Дирихле, или периодическая функция кардинального синуса sinc, определяется как:

для любого ненулевого целого числа .

Эта функция имеет период для нечетных и период для четных . Ее максимальное значение равно 1 для всех , а минимальное −1 для четных . Модуль функции равен произведению и модуля дискретного преобразования Фурье -точечного прямоугольного окна.