dpss
Дискретные вытянутые сфероидальные последовательности (последовательности Слепяна).
| Библиотека |
|
Синтаксис
Вызов функции
-
dpsSeq, lambda = dpss(seqLength, timeHalfBW)— возвращает первуюround(2*timeHalfBW)дискретную вытянутую сфероидальную последовательность (discrete prolate spheroidal sequences, DPSS) длинойseqLengthи отношения концентрации энергииlambdaв частотной области для векторов-столбцовdpsSeq. Эти отношения представляют собой отношение количества энергии в полосе пропускания к полной энергии в диапазоне , где — частота дискретизации.
-
dpsSeq, lambda = dpss(seqLength, timeHalfBW, numSeq)— возвращает первыеnumSeqпоследовательностей DPSS с произведением времени на половину ширины полосы пропусканияtimeHalfBW. Функция возвращает последовательности в порядке их отношений концентрации энергии.
-
dpsSeq, lambda = dpss(___, dpssLength)— интерполирует DPSS последовательности длинойdpssLength.
Аргументы
Входные аргументы
#
seqLength —
длина последовательности
положительное целое число
Details
Длина последовательности, заданная как положительное целое число.
| Типы данных |
|
#
numSeq —
число последовательностей
положительное целое число | двухэлементный вектор
Details
Количество возвращаемых последовательностей, заданное как положительное целое число или двухэлементный вектор. Если указать numSeq как двухэлементный вектор, то выходные последовательности Слепяна будут находиться в диапазоне от numSeq(1) до numSeq(2).
| Типы данных |
|
#
dpssLength —
длина последовательности
положительное целое число
Details
Длина DPSS последовательностей, заданная как положительное целое число.
| Типы данных |
|
Выходные аргументы
#
dpsSeq —
последовательности Слепяна (DPSS)
матрица
Details
Последовательности Слепяна, возвращаемые в виде матрицы с числом строк, равным seqLength, и столбцов, равным round(2*timeHalfBW).
#
lambda —
отношения концентрации энергии в частотной области
вектор-столбец
Details
Отношения концентрации энергии в частотной области, возвращаемые в виде вектора-столбца длиной, равной числу последовательностей Слепяна.
Примеры
Генерация набора последовательностей Слепяна
Details
Построим первые четыре дискретные вытянутые сфероидальные последовательности длиной 512. Зададим произведение времени на половину ширины полосы пропускания равное 2. Построим графики последовательности и отобразим соотношения концентраций.
import EngeeDSP.Functions: dpss
seq_length = 512
time_halfbandwidth = 2
num_seq = 4
dps_seq, lambda = dpss(seq_length, time_halfbandwidth, num_seq)
plot(dps_seq,
title="Slepian Sequences, N = 512, NW = 2",
xlims=(0, 512),
ylims=(-0.15, 0.15),
label=["1st" "2nd" "3rd" "4th"])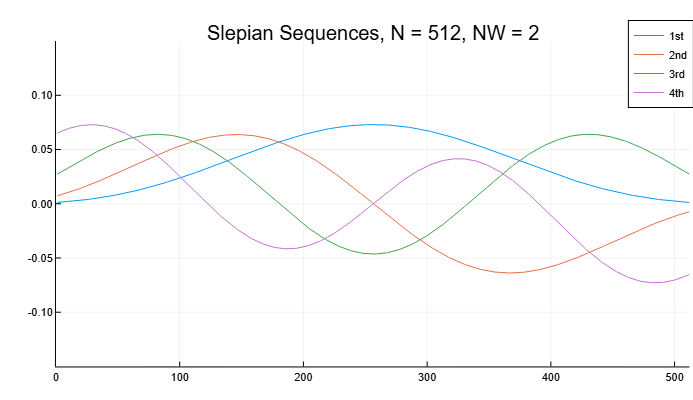
Дополнительно
Дискретные вытянутые сфероидальные последовательности
Details
Дискретные вытянутые сфероидальные последовательности, или последовательности Слепяна, выводятся из следующей задачи о частотно-временной концентрации. Для всех последовательностей с конечной энергией индекс ограничен некоторым множеством , для которого последовательность максимизирует это отношение:
где — частота дискретизации, а . Соответственно, это отношение определяет, какая последовательность с ограниченным индексом имеет наибольшую долю энергии в полосе . Для последовательностей с ограниченным индексом отношение должно удовлетворять неравенству . Последовательность, максимизирующая отношение, — это первая дискретная вытянутая сфероидальная последовательность, или последовательность Слепяна. Вторая последовательность Слепяна максимизирует отношение и ортогональна первой последовательности Слепяна. Третья последовательность Слепяна максимизирует отношение интегралов и ортогональна как первой, так и второй последовательностям Слепяна. Продолжая таким образом, последовательности Слепяна образуют ортогональный набор последовательностей с ограниченной полосой.
Произведение времени на половину ширины полосы пропускания
Details
Произведение времени на половину ширины полосы пропускания равно , где — длина последовательности, а — эффективная ширина полосы пропускания последовательности. При построении последовательностей Слепяна вы выбираете желаемую длину последовательности и ширину полосы пропускания . Как длина последовательности, так и ширина полосы пропускания влияют на количество последовательностей Слепяна с коэффициентами концентрации, близкими к единице. Как правило, существуют последовательностей Слепяна с коэффициентами концентрации энергии, приблизительно равными единице. За пределами последовательностей Слепяна коэффициенты концентрации начинают стремиться к нулю. Распространенные варианты произведения времени на половину ширины полосы пропускания: 2.5, 3, 3.5 и 4.
Вы можете указать ширину полосы пропускания последовательностей Слепяна в Гц, определив произведение времени на половину ширины полосы пропускания как , где — частота дискретизации.