cceps
Комплексный кепстральный анализ.
| Библиотека |
|
Аргументы
Входные аргументы
#
x —
входной сигнал
вещественный вектор
Details
Входной сигнал, заданный как вещественный вектор. Применение линейного фазового члена позволяет избежать скачка фазы на рад. То есть при необходимости он циклически смещается (после дополнения нулями) на несколько отсчетов, чтобы получить нулевую фазу на рад.
#
n —
длина сигнала, дополненного нулями
положительное вещественное целое число
Details
Длина сигнала, дополненного нулями, заданная как положительное вещественное целое число.
Выходные аргументы
#
xhat —
комплексный кепстр
вектор
Details
Комплексный кепстр, возвращаемый в виде вектора.
#
xhat1 —
второй комплексный кепстр
вектор
Details
Второй комплексный кепстр, возвращаемый в виде вектора. Аргумент xhat1 вычисляется с использованием альтернативного алгоритма факторизации, описанного в [1] и [2]. Этот метод применим только к сигналам конечной длительности. В разделе Алгоритмы приведено сравнение методов Фурье и факторизации для вычисления комплексного кепстра.
Примеры
Использование cceps для отображения эха сигнала
Details
В этом примере cceps используется для отображения эха сигнала. Сгенерируем синусоидальный сигнал частотой 45 Гц и дискретизацией 100 Гц. Добавим эхо-сигнал с половиной амплитуды и с задержкой 0.2 с. Вычислим комплексный кепстр сигнала. Обратим внимание на эхо-сигнал с задержкой 0.2 с.
import EngeeDSP.Functions: cceps
Fs = 100
t = 0:1/Fs:1.27
s1 = sin.(2*pi*45*t)
s2 = s1 + 0.5*[zeros(20); s1[1:108]]
c1, nd, c2 = cceps(s2)
plot(t, c1, title="Complex cepstrum", legend=false)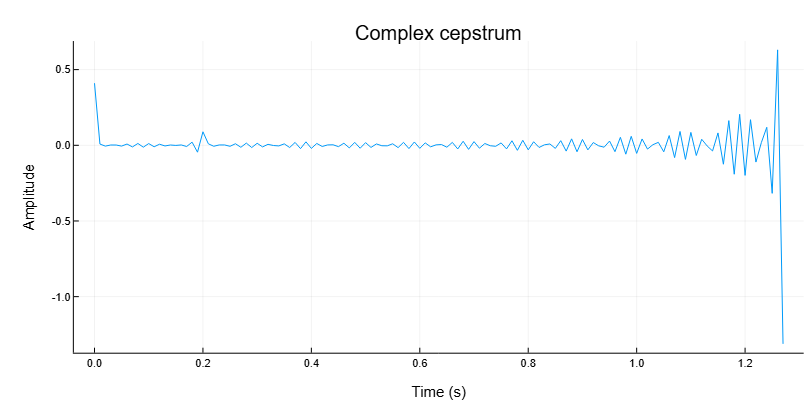
Алгоритмы
Кепстральный анализ — это метод нелинейной обработки сигналов, наиболее часто применяемый в обработке речи и гомоморфной фильтрации [1]. Функция cceps — это реализация алгоритма 7.1 из [3].
В таблице перечислены преимущества и недостатки алгоритмов Фурье и факторизации.
| Алгоритм | Преимущества | Недостатки |
|---|---|---|
Фурье |
Может быть использован для любых сигналов. |
Требуется развертывание фазы. Выходной сигнал низкочастотный. |
Факторизация |
Не требуется развертывание фазы. Нет наложения частот. |
Может использоваться только для кратковременных сигналов. Входной сигнал должен иметь Z-преобразование со всеми нулями, без нулей на единичной окружности. |
В общем случае, результаты этих двух алгоритмов нельзя использовать для взаимной проверки. Их можно использовать для взаимной проверки только в том случае, если первый элемент входных данных положительный, Z-преобразование последовательности данных содержит только нули, все эти нули находятся внутри единичной окружности, а входная последовательность данных длинная (или дополнена нулями).
Литература
-
Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice Hall, 1999, pp. 788–789.
-
Steiglitz, K., and B. Dickinson. Computation of the Complex Cepstrum by Factorization of the Z-transform. Proceedings of the 1977 IEEE® International Conference on Acoustics, Speech and Signal Processing, pp. 723–726.
-
Digital Signal Processing Committee of the IEEE Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979.