Базовые примеры формальной верификации в Engee

Блок Chart модели promela_a.engee содержит единственное состояние A.

Узнать, активно состояние A или нет, можно по значению глобальной переменной promela_a_S.Chart.state.A.is_active в сгенерированном файле promela_a.pml.

Об активности Chart также можно судить по значению глобальной переменной promela_a_S.Chart.state.is_active.

С помощью препроцессора назначим этим переменным сокращенные псевдонимы для использования в формулах спецификации:

и добавим их вместе со спецификациями:

в конец файла promela_a.pml.

Произведем верификацию спецификаций:

Консольный вывод программы Spin показывает, что каждая из спецификаций выполняется — верификация прошла успешно.

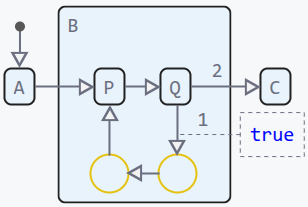
Модель abcpq.engee на рисунке имеет три особенности:

Попробуем проверить эти утверждения.

Как обычно, объявим сокращенные псевдонимы для переменных, определяющих активность наших состояний. Для этого добавим в файл abcpq.pml секцию макросов препроцессора:

Специфицировать недостижимость состояния C можно формулой «всегда не C», проверка которой, как и ожидается, проходит успешно:

Эту спецификацию можно считать свойством безопасности (safety) □p для формулы p, запрещающей состоянию C активизироваться (то есть p = ¬C).

Однако если заменить в формуле выше имя c на q:

то верификация измененной формулы ожидаемо завершится ошибкой, так как изначально было очевидно, что состояние Q достижимо:

Контрпример, полученный из файла трассы:

где следует обратить внимание на строку, указывающую на присваивание, которого, согласно спецификации, не должно быть:

и строку с противоречащим спецификации значением переменной в конце трассы:

Теперь проверим свойство живости (liveness) — необходимость когда-либо стать активным:

Результат верификации:

Здесь исследование трассы неэффективно: контрпример, очевидно, бесконечен.

А вот свойства живости ◊A ∧ ◊B ∧ ◊P ∧ ◊Q остальных состояний верифицируются успешно:

Также с помощью LTL можно верифицировать свойство справедливости (fairness) □◊P или □◊Q, то есть требование, что событие (активизация P или Q) будет происходить бесконечно часто:

и свойство стабилизации (stabilization) ◊□B — требование, что некоторое событие (активность тупикового B) рано или поздно наступит навсегда:

С помощью импликации и исключающего «ИЛИ» можно специфицировать корреляцию активности родительского и дочерних состояний:

Вместо импликации можно использовать отношение эквивалентности:

Комбинируя импликацию и оператор neXt, можно убедиться, что активность состояний P и Q осциллирует с периодичностью 1 шаг:

Рассмотрим еще одну простую модель ab.engee, проверка свойств которой в режиме прямой симуляции может занять значительное время, тогда как формальная верификация тех же свойств выполняется практически мгновенно.

Переход между состояниями A и B выполняется после того, как переменная i увеличится миллиард раз.

Объявим сокращенные имена:

Формула, верифицирующая факт обязательного перехода между состояниями A и B когда-нибудь в будущем:

Убедимся, что этот переход не может происходить на каждом шаге; более сильная спецификация приведет к ошибке:

Оператор until также успешно верифицируется «когда-нибудь в будущем»:

Учитывая, что оператор становится истинным сразу после активизации блока Chart, можно записать более строго:

Или эквивалентно, но короче:

Более слабая форма также успешно верифицируется:

А оператор «освобождения» (release) приводит к ошибке, так как состояния A и B не могут быть активны одновременно:

Проверим те же свойства, используя значения выходных переменных блока Chart x и y, изначально установленных в false:

И в заключение проверим диапазон значений переменной i.

В начальный момент времени значение переменной i равно 0:

Значение i всегда лежит в диапазоне [0..1000000001]:

Когда-либо i принимает свое максимальное значение 1000000001: