Идентификация нелинейных моделей

Этот пакет поддерживает две формы идентификации нелинейных систем.

Оценка параметров в известной структуре модели (линейной или нелинейной) , где p — вектор оцениваемых параметров.
Оценка моделей Гаммерштейна — Винера, то есть линейных систем со статическими нелинейными функциями на входе и (или) выходе.

Оценка параметров в известной структуре модели

Оценка параметров в дифференциальных уравнениях может производиться путем формирования предиктора на один шаг для выхода и минимизации погрешности прогнозирования. Эта процедура упакована в функцию ControlSystemIdentification.nonlinear_pem, которая доступна в виде расширения пакета при установке и загрузке пакета LeastSquaresOptim.jl пользователем вручную.

Ниже описывается порядок использования этой функции.

Динамика задается в форме или , где — это состояние, — вход, p — вектор оцениваемых параметров, а — время.
Если динамика описывается в непрерывном времени (дифференциальным или дифференциально-алгебраическим уравнением), используйте пакет SeeToDee.jl для ее дискретизации. Если динамика уже дискретизирована, пропустите этот шаг.
Определите функцию измерения , сопоставляющую состояние и вход с измеренным выходом.
Укажите ковариантность шума динамики и шума измерения наподобие того, как это делается при построении фильтра Калмана для линейной системы.
Произведите оценку с помощью функции ControlSystemIdentification.nonlinear_pem.

На внутреннем уровне функция ControlSystemIdentification.nonlinear_pem создает сигма-точечный фильтр Калмана (UKF) из пакета LowLevelParticleFilters.jl с целью оценки состояния по указанной траектории данных. Затем решается задача оптимизации с целью нахождения параметров (и, возможно, начального условия), при которых погрешности прогнозирования минимальны. Эта процедура немного отличается от простого нахождения параметров, при которых чистая модель системы соответствует данным. В частности, подход на основе погрешности прогнозирования обычно позволяет справляться с очень плохими начальными предположениями, нестабильными и даже хаотичными системами. Дополнительные сведения о методе на основе погрешности прогнозирования см. в руководстве Особенности метода на основе погрешности прогнозирования.

# ControlSystemIdentification.nonlinear_pem — Function

nonlinear_pem(
    d::IdData,
    discrete_dynamics,
    measurement,
    p0,
    x0,
    R1,
    R2,
    nu;
    optimizer = LevenbergMarquardt(),
    λ = 1.0,
    optimize_x0 = true,
    kwargs...,
)

Нелинейный метод на основе ошибки прогнозирования (PEM).

Этот метод пытается найти оптимальный вектор параметров p и начальное условие x_0, которое минимизирует сумму ошибок одношагового прогнозирования методом квадратов. Прогнозирование осуществляется с помощью сигма-точечного фильтра Калмана (UKF), а оптимизация — с помощью метода Гаусса — Ньютона.

!!! info "Requires LeastSquaresOptim.jl" Эта функция доступна только в том случае, если пользователь вручную установил и загрузил пакет LeastSquaresOptim.jl.

Аргументы

d: идентификационные данные
discrete_dynamics: Функция динамики (xₖ, uₖ, p, t) -> x(k+1), которая принимает текущее состояние x, входное значение u, параметры p и время t и возвращает следующее состояние x(k+1).
measurement: Функция измерения/выходная функция нелинейной системы (xₖ, uₖ, p, t) -> yₖ
p0: начальное предположение для вектора параметров.
x0: начальное предположение для начального условия
R1: ковариационная матрица шума динамики (при увеличении этого параметра алгоритм меньше доверяет модели)
R2: ковариационная матрица шума измерений (при увеличении этого параметра алгоритм меньше доверяет модели)
nu: количество входных данных для системы
optimizer: Любой оптимизатор из LeastSquaresOptim
λ: Весовой коэффициент для минимизации dot(e, λ, e. Обычно используется метрика λ = Diagonal(1 ./ (mag.^2)), где mag — это вектор типичной величины каждого выходного значения. Изначально квадратный корень из W = sqrt(λ) вычисляется таким образом, чтобы остатки, хранящиеся в res, были равны W*e.
optimize_x0: Следует ли оптимизировать начальное условие x0. Если задано false, для начального условия фиксируется значение x0 и оптимизация производится только по параметрам p.

Внутренний оптимизатор принимает ряд именованных аргументов:

lower: нижние границы для параметров и начального условия (если оптимизировано). Если x0 оптимизировано, это будет вектор со структурой [lower_p; lower_x0].
upper: верхние границы для параметров и начального условия (если оптимизировано). Если x0 оптимизировано, это будет вектор со структурой [upper_p; upper_x0].
x_tol = 1e-8
f_tol = 1e-8
g_tol = 1e-8
iterations = 1_000
Δ = 10.0
store_trace = false

Дополнительные сведения см. в разделе Идентификация нелинейных моделей.

!!! warning "Experimental" Эта функция считается экспериментальной и может измениться в будущем без учета семантического управления версиями. В этой реализации также отсутствует ряд функций, присущих хорошим нелинейным реализациям PEM, таких как регуляризация и поддержка нескольких наборов данных.

Пример: Четыре сосуда

В этом примере, изображенном на схеме ниже, рассматривается система из четырех сосудов: жидкость из двух верхних сосудов поступает в два нижних. Система из четырех сосудов является хорошо изученным примером, который часто приводится в курсах по многопараметрическому управлению. В частности, данный вариант системы взят из вводного курса по автоматическому управлению Лундского университета.

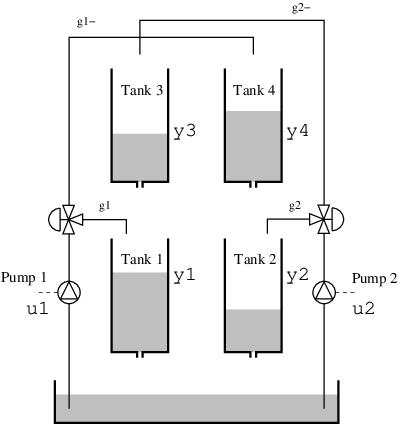
Процесс характеризуется наличием перекрестной связи между сосудами, которая регулируется параметром : Подача от насосов разделяется согласно параметрам ]. Подача в сосуд 1 составляет , а подача в сосуд 4 — . Сосуды 2 и 3 являются симметричными.

Динамика описывается формулой:

где — уровни жидкости в сосудах, а — площади поперечного сечения выпускных отверстий соответствующих сосудов.

Начнем с определения динамики в непрерывном времени, а затем дискретизируем ее с помощью интегратора SeeToDee.Rk4 с временем дискретизации .

using StaticArrays, SeeToDee

function quadtank(h, u, p, t)
    k1, k2, g = p[1], p[2], 9.81
    A1 = A3 = A2 = A4 = p[3]
    a1 = a3 = a2 = a4 = 0.03
    γ1 = γ2 = p[4]

    ssqrt(x) = √(max(x, zero(x)) + 1e-3) # Для числовой устойчивости при x = 0

    SA[
        -a1/A1 * ssqrt(2g*h[1]) + a3/A1*ssqrt(2g*h[3]) +     γ1*k1/A1 * u[1]
        -a2/A2 * ssqrt(2g*h[2]) + a4/A2*ssqrt(2g*h[4]) +     γ2*k2/A2 * u[2]
        -a3/A3*ssqrt(2g*h[3])                          + (1-γ2)*k2/A3 * u[2]
        -a4/A4*ssqrt(2g*h[4])                          + (1-γ1)*k1/A4 * u[1]
    ]
end
measurement(x,u,p,t) = SA[x[1], x[2]]

Ts = 1.0
discrete_dynamics = SeeToDee.Rk4(quadtank, Ts, supersample=2)

SeeToDee.Rk4{typeof(Main.quadtank), Float64}(Main.quadtank, 1.0, 2)

Выходом этой системы является уровень воды в первых двух сосудах, то есть ].

Кроме того, укажем количество переменных состояния, входов и выходов, а также вектор «истинных» параметров, то есть тех, которые мы будем пытаться оценить.

nx = 4
ny = 2
nu = 2
p_true = [1.6, 1.6, 4.9, 0.2]

4-element Vector{Float64}:
 1.6
 1.6
 4.9
 0.2

Затем смоделируем данные системы, которые будут использоваться для идентификации:

using ControlSystemIdentification, ControlSystemsBase
using ControlSystemsBase.DemoSystems: resonant
using LowLevelParticleFilters
using LeastSquaresOptim
using Random, Plots, LinearAlgebra

# Генерируем выходные данные системы
Random.seed!(1)
Tperiod = 200
t = 0:Ts:1000
u1 = vcat.(0.25 .* sign.(sin.(2pi/Tperiod .* (t ./ 40).^2)) .+ 0.25)
u2 = vcat.(0.25 .* sign.(sin.(2pi/Tperiod .* (t ./ 40).^2 .+ pi/2)) .+ 0.25)
u  = vcat.(u1,u2)
u = [u; 0 .* u[1:100]]
x0 = [2.5, 1.5, 3.2, 2.8]
x = LowLevelParticleFilters.rollout(discrete_dynamics, x0, u, p_true)[1:end-1]
y = measurement.(x, u, 0, 0)
y = [y .+ 0.5randn(ny) for y in y] # Добавляем шум измерения
Y = reduce(hcat, y) # Преобразуем вектор векторов в матрицу
U = reduce(hcat, u) # Преобразуем вектор векторов в матрицу
plot(
    plot(reduce(hcat, x)', title="States", lab=["h1" "h2" "h3" "h4"]),
    plot(U', title="Inputs", lab=["u1" "u2"]),
    plot(Y', title="Outputs", lab=["y1" "y2"]),
)

PgxnU7v3btXrAiC8Pr163fv3lEU1dzcLD6lTn6dp0+ffv78+fDhw+QK+69LpVLi44AAoNPpyLwxAMzMzCwvL9tsNrPZLDbIZDJTU1MKhcLhcJT2ZjgcXlxcPHDgALmcRQj931XuQIgQQghJoBLXCBFCCCHJ4ECIEEKoquFAiBBCqKrhQIgQQqiq4UCIEEKoquFAiBBCqKrhQIgQQqiq4UCIEEKoquFAiBBCqKrhQIgQQqiq4UCIEEKoqv0DNuHbiqO18l0AAAAASUVORK5CYII=

Как обычно, экспериментальные данные упаковываются в объект iddata. Наконец, мы указываем ковариационные матрицы для шума динамики и шума измерения, а также предположительное начальное условие. Так как мы можем измерить уровень в первых двух сосудах, для них используется истинное начальное условие, но для последних двух сосудов мы берем достаточно далекое от истины предположительное начальное условие.

Выбор ковариационных матриц может быть нетривиальной задачей. Общее представление можно получить в записи блога о настройке фильтра Калмана. В данном случае мы выбираем для некоторое значение, которое представляется разумным, а для намеренно выбираем большое значение. Выбор большой ковариации для шума измерения приводит к тому, что средство оценки состояния будет меньше доверять результатам измерения, что, в свою очередь, приводит к меньшей коррекции по обратной связи. В результате алгоритм будет отдавать предпочтение модели, обеспечивающей хорошее качество симуляции, а не ограничиваться одношаговым прогнозированием.

Наконец, мы вызываем функцию ControlSystemIdentification.nonlinear_pem, чтобы выполнить оценку.

d = iddata(Y, U, Ts)
x0_guess = [2.5, 1.5, 1, 2] # Предположительное начальное условие
p_guess = [1.4, 1.4, 5.1, 0.25] # Начальное предположение для параметров

R1 = Diagonal([0.1, 0.1, 0.1, 0.1])
R2 = 100*Diagonal(0.5^2 * ones(ny))

model = ControlSystemIdentification.nonlinear_pem(d, discrete_dynamics, measurement, p_guess, x0_guess, R1, R2, nu)

NonlinearPredictionErrorModel
  p: [1.6130595662288096, 1.599457420302662, 4.886961965817006, 0.20432997287915136]
  x0: [2.558506451200765, 1.6722780052530595, 2.878022716639319, 2.092408142173953]
  Ts: 1.0
  ny = 2, nu = 2, nx = 4

После этого можно проверить работу модели на основе данных и сравнить результат с моделью, соответствующей начальному предположению.

simplot(model, d, layout=2)

x_guess = LowLevelParticleFilters.rollout(discrete_dynamics, x0_guess, u, p_guess)[1:end-1]
y_guess = measurement.(x_guess, u, 0, 0)
plot!(reduce(hcat, y_guess)', lab="Initial guess")

4ADB1kIM6BYUQAACAWYNdowAAAMwaFEIAAABmDQohAAAAswaFEAAAgFn7X4yxUKebZL5aAAAAAElFTkSuQmCC

Можно также провести остаточный анализ, чтобы выяснить, отражает ли модель динамику системы.

residualplot(model, d)

NW1a9cKCgquX78uk8n69+8fHBzc0SVCyC9hIEQIIdSlYRshQgihLg0DIUIIoS4NAyFCCKEu7f8D3bhp2ocKk3YAAAAASUVORK5CYII=

Так как здесь используются сгенерированные данные, остатки являются белыми и беспокоиться не о чем. На практике всегда следует проверять остатки для выявления систематических ошибок в модели.

Возвращаемый объект модели содержит оцениваемые параметры. Давайте посмотрим, насколько они приемлемы.

[p_true p_guess model.p]

4×3 Matrix{Float64}:
 1.6  1.4   1.61306
 1.6  1.4   1.59946
 4.9  5.1   4.88696
 0.2  0.25  0.20433

Как и следовало ожидать, оцениваемые параметры близки к истинным.

Настроить реализацию нелинейного метода на основе погрешности измерения можно с помощью низкоуровневого интерфейса, используемого в руководстве в документации по LowLevelParticleFilters.jl. Он также предоставляет реализацию фильтра UKF.

Оценка Гаммерштейна — Винера

Этот пакет предоставляет элементарную реализацию для идентификации нелинейных систем в форме Гаммерштейна — Винера, то есть систем со статическими нелинейными входами, статическими нелинейными выходами и линейной системой между ними, где нелинейности известны. Единственным аспектом нелинейностей, который может оцениваться, являются параметры. Выражаясь более формально, метод оценки newpem позволяет оценить модель следующей формы:

   ┌─────┐   ┌─────┐   ┌─────┐
 u │     │uₙₗ│     │ y │     │ yₙₗ
──►│  gᵢ ├──►│  P  ├──►│  gₒ ├─►
   │     │   │     │   │     │
   └─────┘   └─────┘   └─────┘

где g_i и g_o — это статические нелинейные функции, которые могут зависеть от некоторого параметра векторов , оптимизируемого вместе с матрицами . Порядок оценки такой модели подробно описывается в docstring функции newpem.

Результатом данной оценки является линейная система без применения нелинейностей, которые должны обрабатываться пользователем вручную.

Используемый по умолчанию оптимизатор BFGS может испытывать проблемы с решением задач, включающих нелинейности. Если результаты недостаточно хороши, попробуйте другой оптимизатор, например optimizer = Optim.NelderMead().

Пример с имитированными данными:

В приведенном ниже примере идентифицируется модель колебательной системы, знак выхода которой неизвестен, то есть нелинейность выхода задается в виде . Чтобы пример был немного реалистичнее, также имитируется цветной шум измерения и входа, yn и un. Пример с реальными данными см. в разделе Оценка Гаммерштейна — Винера для нелинейной системы ременного привода.

using ControlSystemIdentification, ControlSystemsBase
using ControlSystemsBase.DemoSystems: resonant
using Random, Plots

# Генерируем выходные данные системы
Random.seed!(1)
T = 200
sys = c2d(resonant(ω0 = 0.1) * tf(1, [0.1, 1]), 1)# generate_system(nx, nu, ny)
nx = sys.nx
nu = 1
ny = 1
x0 = zeros(nx)
sim(sys, u, x0 = x0) = lsim(sys, u, 1:T, x0 = x0)[1]
sysn = c2d(resonant(ω0 = 1) * tf(1, [0.1, 1]), 1)

σu = 1e-2 # Среднеквадратичное отклонение входного шума
σy = 1e-3 # Среднеквадратичное отклонение выходного шума

u  = randn(nu, T)
un = u + sim(sysn, σu * randn(size(u)), 0 * x0)
y  = sim(sys, un, x0)
yn = y + sim(sysn, σy * randn(size(u)), 0 * x0)

# Нелинейное преобразование выхода
ynn = abs.(yn)
d  = iddata(ynn, un, 1)
output_nonlinearity = (y, p) -> y .= abs.(y)

# Оцениваем 10 моделей со случайной инициализацией (каждый раз разной) и выбираем лучшую
# Если результаты неудовлетворительные, попробуйте использовать вместо этого `optimizer = Optim.NelderMead()`
results = map(1:10) do _
    sysh, x0h, opt = newpem(d, nx; output_nonlinearity, show_trace=false, focus = :simulation)
    (; sysh, x0h, opt)
end;

(; sysh, x0h, opt) = argmin(r->r.opt.minimum, results) # Находим модель с наименьшей стоимостью

yh = simulate(sysh, d, x0h)
output_nonlinearity(yh, nothing) # Необходимо вручную применить нелинейность выхода к прогнозу
plot(d.t, [abs.(y); u]', lab=["True nonlinear output" "Input"], seriestype = [:line :steps], layout=(2,1), xlabel="Time")
scatter!(d.t, ynn', lab="Measured nonlinear output", sp=1)
plot!(d.t, yh', lab="Simulation", sp=1, l=:dash)

Видеоруководства

Соответствующие видеоруководства доступны здесь: