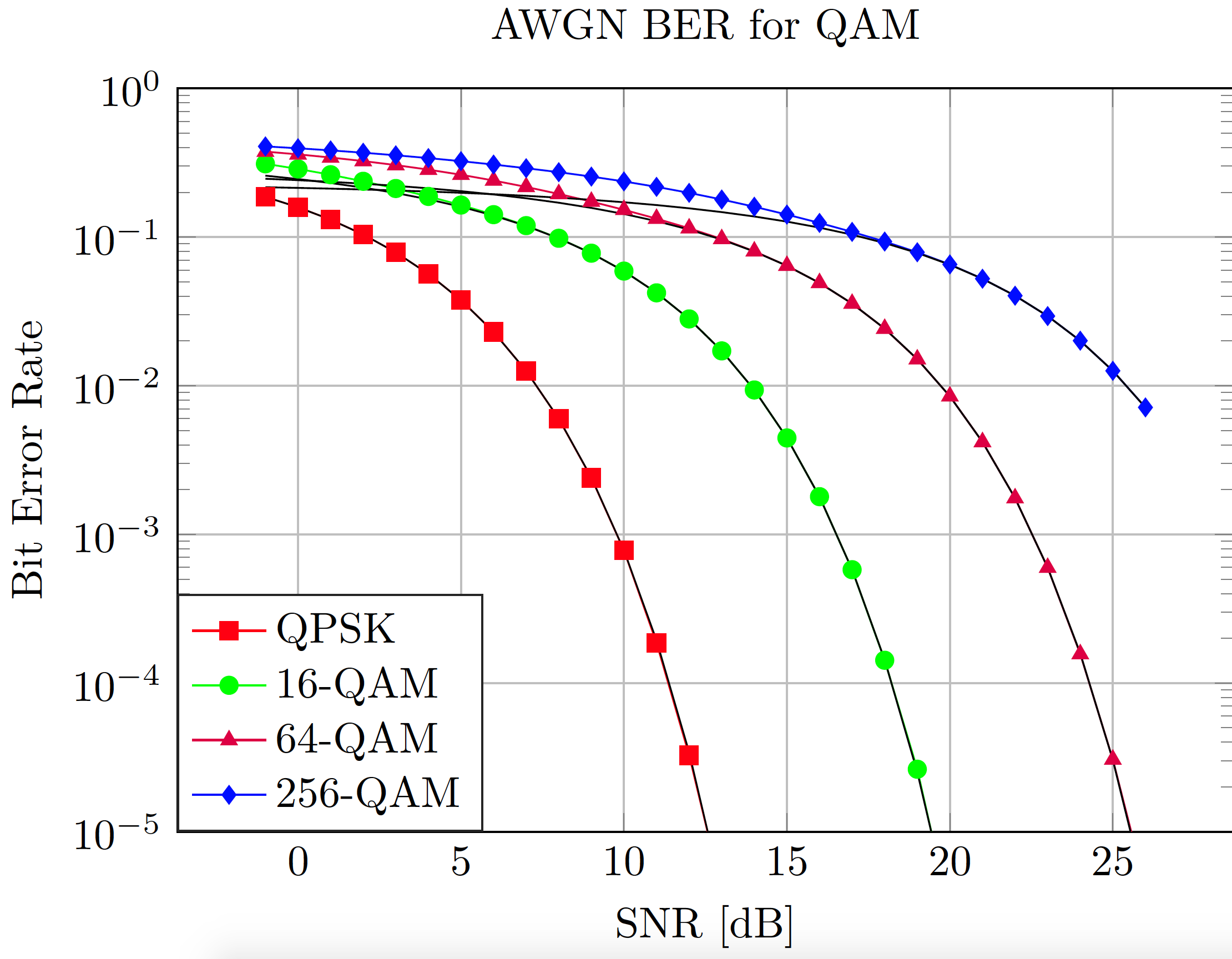
Вычисление теоретического BER для канала AWGN и различных размеров созвездий
Основываясь на предыдущих данных, мы можем рассчитать итерационный набор тестов для вычисления коэффициента битовых ошибок для различных размеров созвездий и сравнить результаты моделирования с теорией. В качестве напоминания: теоретический коэффициент битовых ошибок может быть аппроксимирован как
Для начала вызовем модули.
using DigitalComm using PGFPlotsX
Сначала определим основную функцию Монте-Карло, которая вычисляет элементарный канал Tx-Rx и возвращает количество ошибок и количество вычисленных битов (подлежащих накоплению).
function monteCarlo(snr,mcs,nbSymb) # Количество битов nbBits = nbSymb * Int(log2(mcs)); # --- Генерация двоичной последовательности bitSeq = genBitSequence(nbBits); # --- Сопоставление QPSK qamSeq = bitMappingQAM(mcs,bitSeq); # ---------------------------------------------------- # --- Канал # ---------------------------------------------------- # --- AWGN # Теоретическая мощность равна 1 (нормализованное созвездие) qamNoise, = addNoise(qamSeq,snr,1); # ---------------------------------------------------- # --- Этап Rx: SRRC # ---------------------------------------------------- # --- Блок двоичной распаковки bitDec = bitDemappingQAM(mcs,qamNoise); # --- Счетчик ошибок nbE = sum(xor.(bitDec,bitSeq)); # --- Возвращает ошибки и биты return (nbE,nbBits); end
Функция для построения графика зависимости BER по сравнению с SNR для различных mcs и сравнения с теорией
function doPlot(snrVect,ber,qamVect)
a = 0;
@pgf a = Axis({
ymode = "log",
height ="3in",
width ="4in",
grid,
xlabel = "SNR [dB]",
ylabel = "Bit Error Rate ",
ymax = 1,
ymin = 10.0^(-5),
title = "AWGN BER for QAM",
legend_style="{at={(0,0)},anchor=south west,legend cell align=left,align=left,draw=white!15!black}"
},
Plot({color="red",mark="square*"},Table([snrVect,ber[1,:]])),
LegendEntry("QPSK"),
Plot({color="green",mark="*"},Table([snrVect,ber[2,:]])),
LegendEntry("16-QAM"),
Plot({color="purple",mark="triangle*"},Table([snrVect,ber[3,:]])),
LegendEntry("64-QAM"),
Plot({color="blue",mark="diamond*"},Table([snrVect,ber[4,:]])),
LegendEntry("256-QAM"),
);
# --- Добавление теоретической кривой
snrLin = (10.0).^(snrVect/10)
for qamScheme = qamVect
ebNo = snrLin / log2(qamScheme);
# Эта аппроксимация справедлива только для высокого показателя SNR (ошибка в одном символе преобразуется в ошибку в одном бите с помощью кодирования Грея).
berTheo = 4 * ( 1 - 1 / sqrt(qamScheme)) / log2(qamScheme) * qFunc.(sqrt.( 2*ebNo * 3 * log2(qamScheme) / (2*(qamScheme-1) )));
@pgf push!(a,Plot({color="black"},Table([snrVect,berTheo])));
end
display(a);
end
Далее, основная процедура вычисления BER для заданного количества итераций и диапазона SNR
function main() # --- Параметры nbIt = 10000; # Количество итераций nbSymb = 1024; # Количество символов на итерацию mcs = [4,16,64,256]; # Размер созвездия snrRange = (-1:26); # SNR в дБ # --- Начальные показатели производительности nbSNR = length(snrRange); ber = zeros(Float64,length(mcs),nbSNR); for iMcs = 1 : 1 : length(mcs) for iSNR = 1 : 1 : nbSNR # --- Создание счетчиков BER nbE = 0; nbB = 0; for iN = 1 : 1 : nbIt # --- Элементарный вызов MC # Соответствует заданному SNR и заданной итерации # Поскольку мы эргодичны в AWGN, для вычисления BER имеет значение только nbSymb*nbIt. (a,b) = monteCarlo(snrRange[iSNR],mcs[iMcs],nbSymb); # --- Обновление счетчиков nbE += a; # Ошибки приращения nbB += b; # Инкрементные счетчики битов end ber[iMcs,iSNR] = nbE / nbB; end end # --- Процедура построения графиков doPlot(snrRange,ber,mcs); end
Получился следующий график, демонстрирующий адекватность теории и практики для высоких показателей SNR (теоретическая кривая построена при предположении, что ошибка в одном символе приводит к одному ошибочному биту (кодирование Грея), что верно только при средних уровнях шума).