Документация Engee

Предобусловливание

Методы GradientDescent, ConjugateGradient и LBFGS поддерживают предобусловливание. Предобусловливатель можно представить как изменение координат, при котором гессиан становится лучше обусловленным. При использовании хорошего предобусловливателя можно существенно улучшить сходимость.

Предобусловливатель P может иметь любой тип, если реализованы следующие два метода:

  • A_ldiv_B!(pgr, P, gr): применяет P к вектору gr и сохраняет в pgr (интуитивно, pgr = P \ gr)

  • dot(x, P, y): внутреннее произведение, создаваемое P (интуитивно, dot(x, P * y))

То, что именно означают эти операции, зависит от того, как хранится P. Обычно мы храним матрицу P, которая аппроксимирует гессиан в некотором туманном смысле. В данном случае

  • A_ldiv_B!(pgr, P, gr) = copyto!(pgr, P \ A)

  • dot(x, P, y) = dot(x, P * y)

Наконец, предобусловливатель можно обновлять по мере изменения переменной состояния x. Для этого используется precondprep!, который передается оптимизаторам как именованный аргумент. Например,

   method=ConjugateGradient(P = precond(100), precondprep! = precond(100))

хотя в этом случае он всегда будет возвращать одну и ту же матрицу. (Более естественный пример см. в описании fminbox.jl.)

Помимо предобусловливания для матриц, Optim.jl предоставляет тип InverseDiagonal, который представляет диагональную матрицу по ее обратным элементам.

Пример

Ниже мы видим пример минимизации функции без применения предобусловливателя и с ним.

using ForwardDiff, Optim, SparseArrays
initial_x = zeros(100)
plap(U; n = length(U)) = (n-1)*sum((0.1 .+ diff(U).^2).^2 ) - sum(U) / (n-1)
plap1(x) = ForwardDiff.gradient(plap,x)
precond(n) = spdiagm(-1 => -ones(n-1), 0 => 2ones(n), 1 => -ones(n-1)) * (n+1)
f(x) = plap([0; x; 0])
g!(G, x) = copyto!(G, (plap1([0; x; 0]))[2:end-1])
result = Optim.optimize(f, g!, initial_x, method = ConjugateGradient(P = nothing))
result = Optim.optimize(f, g!, initial_x, method = ConjugateGradient(P = precond(100)))

Первый вызов оптимизации сходится медленнее, чем второй. Взглянув на график двумерной версии функции, можно увидеть, в чем проблема.

plap

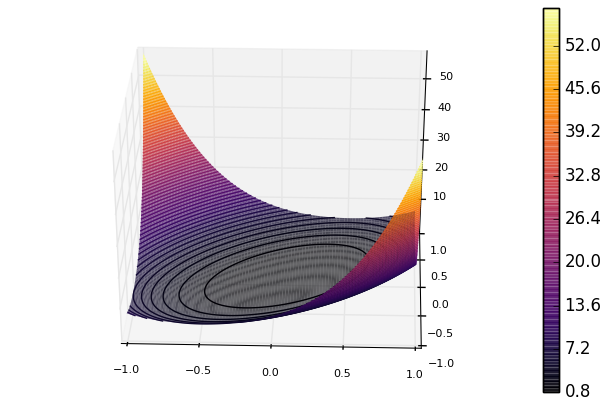
Контуры имеют форму эллипсоидов, но нам бы хотелось, чтобы это были круги. Использование предобусловливателя позволяет изменять координаты таким образом, что контуры становятся менее эллипсоидоподобными. Тесты производительности показывают, что использование предобусловливания обеспечивает приблизительное 15-кратное ускорение в этом 100-мерном случае.

Справочные материалы