PID Controller
ПИД-регулятор.
Тип: PIDController
PID Controller Путь в библиотеке: |
|
Discrete PID Controller Путь в библиотеке: |
Описание
Блок PID Controller реализует ПИД-регулятор (ПИД, ПИ, ПД, только П или только И).
Выход блока является взвешенной суммой входного сигнала, интеграла входного сигнала и производной входного сигнала. Веса суммирования задаются пропорциональными, интегральными и дифференциальными коэффициентами. Полюс первого порядка фильтрует дифференциальную составляющую.
Блок поддерживает несколько типов и структур регулятора. Возможные варианты:
-
Тип регулятора (ПИД, ПИ, ПД, только П или только И).
-
Форма регулятора (параллельная или идеальная).
-
Временная область (непрерывная или дискретная).
-
Начальные условия.
При изменении этих параметров изменяется внутренняя структура блока: активируются соответствующие варианты подсистем.
Порты
Вход
#
IN_1
—
входной сигнал
скаляр | вектор | матрица
Details
Разница между уставкой и выходным сигналом управляемой системы, как показано на рисунке ниже:
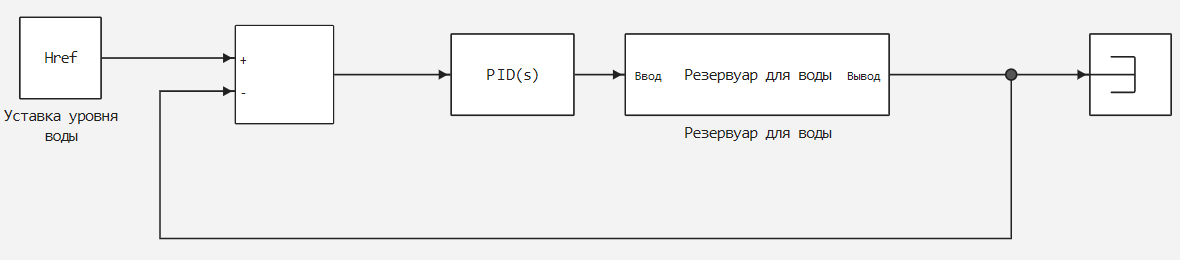
| Типы данных |
|
| Поддержка комплексных чисел |
Нет |
Выход
#
OUT_1
—
выход регулятора
скаляр | вектор
Details
Выход регулятора, представляющий собой взвешенную сумму входного сигнала, интеграла входного сигнала и производной входного сигнала. Весы суммирования задаются пропорциональным, интегральным и дифференциальным коэффициентами. Какие слагаемые участвуют в суммировании, зависит от значения параметра Controller.
Выход регулятора является векторным сигналом, когда вход является векторным сигналом. В этом случае блок действует как независимых ПИД-регуляторов, где — количество сигналов во входном векторе.
| Типы данных |
|
| Поддержка комплексных чисел |
Нет |
Параметры
Основные
#
Controller —
тип регулятора
PID | PI | PD | P | I
Details
Задает состав регулятора:
-
PID— пропорциональная, интегральная и дифференциальная части. -
PI— только пропорциональная и интегральная части. -
PD— только пропорциональная и дифференциальная части. -
P— только пропорциональная часть. -
I— только интегральная часть.
| Значения |
|
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Нет |
#
Time domain —
регулятор дискретного или непрерывного времени
Discrete-time | Continuous-time
Details
Для значения Discrete-time рекомендуется явно задать шаг расчета для блока. При выборе значения Discrete-time также включаются параметры Integrator method и Filter method.
Когда блок PID Controller находится в модели с синхронным управлением состоянием, вы не можете выбрать Continuous-time.
| Значения |
|
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Нет |
#
Sample time —
интервал между шагами расчета
SampleTime (real number / vector of two real numbers)
Details
Укажите интервал между шагами расчета как неотрицательное число. Чтобы наследовать шаг расчета, установите для этого параметра значение −1.
Рекомендуется явно задать шаг расчета регулятора, особенно если ожидается, что шаг расчета последующих блоков изменится. Влияние коэффициентов регулятора , , и зависит от шага расчета. Таким образом, для заданного набора значений коэффициентов изменение шага расчета изменяет производительность регулятора.
Зависимости
Чтобы использовать этот параметр, установите для параметра Time domain значение Discrete-time.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |
#
Form —
структура регулятора
Parallel | Ideal
Details
Задает, является ли структура регулятора параллельной или идеальной:
-
Parallel— выход регулятора представляет сумму пропорциональной, интегральной и дифференциальной частей, независимо взвешенных по , и соответственно. Например, для ПИД-регулятора параллельной формы с непрерывным временем передаточная функция имеет вид:.
Для регулятора параллельной формы с дискретным временем передаточная функция имеет вид:
,
где параметры Integrator method и Filter method определяют и соответственно.
-
Ideal— пропорциональное усиление действует на сумму всех частей. Например, для ПИД-регулятора идеальной формы с непрерывным временем передаточная функция имеет вид:Для регулятора идеальной формы с дискретным временем передаточная функция имеет вид:
,
где параметры Integrator method и Filter method определяют и соответственно.
| Значения |
|
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Нет |
Параметры регулятора
#
Proportional (P) —
пропорциональный коэффициент
Real number
Details
Конечное вещественное значение пропроционального коэффициента. Когда Form:
-
Parallel— пропорциональное действие не зависит от интегрального и производного воздействий. Например, для параллельного ПИД-регулятора с непрерывным временем передаточная функция имеет вид:.
Для регулятора параллельной формы с дискретным временем передаточная функция имеет вид:
,
где параметры Integrator method и Filter method определяют и соответственно.
-
Ideal— пропорциональный коэффициент применяется к сумме всех частей. Например, для ПИД-регулятора идеальной формы с непрерывным временем передаточная функция имеет вид:.
Для регулятора идеальной формы с дискретным временем передаточная функция имеет вид:
,
где параметры Integrator method и Filter method определяют и соответственно.
Зависимости
Чтобы использовать этот параметр, установите для параметра Controller значение PID, PI, PD или P.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |
#
Integral (I) —
интегральный коэффициент
Real number
Details
Конечное вещественное значение интегрального коэффициента.
Зависимости
Чтобы использовать этот параметр, установите для параметра Controller значение PID, PI или I.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |
#
Derivative (D) —
дифференциальный коэффициент
Real number
Details
Конечное вещественное значение дифференциального коэффициента.
Зависимости
Чтобы использовать этот параметр, установите для параметра Controller значение PID или PD.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |
#
Filter coefficient (N) —
коэффициент фильтрации производной
Real number
Details
Конечное вещественное значение коэффициента усиления фильтра. Коэффициент фильтра определяет положение полюса фильтра в дифференциальной части блока. Расположение полюса фильтра зависит от параметра Time domain.
Когда Time domain имеет значение Continuous-time, положение полюса равно s = −N.
Когда Time domain имеет значение Discrete-time, положение полюса зависит от параметра Filter method.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |
#
Use filtered derivative —
применить фильтр к производной
Logical
Details
Только для ПИД-регуляторов с дискретным временем: снимите этот флажок, чтобы заменить отфильтрованную производную нефильтрованным значением. В этом случае дифференциальный член передаточной функции регулятора станет:
.
Для ПИД-регуляторов с непрерывным временем производная составляющая всегда фильтруется.
Зависимости
Чтобы использовать этот параметр, установите для параметра Time domain значение Discrete-time, а для параметра Controller значение PID или PD.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Нет |
Методы интегрирования и фильтрации
#
Integrator method —
метод интегрирования в дискретном регуляторе
Forward Euler | Backward Euler | Trapezoidal
Details
В дискретном времени интегральный член передаточной функции регулятора равен , где зависит от метода интегрирования:
-
Forward Euler— прямая прямоугольная (левая) аппроксимация:.
Этот метод лучше всего подходит для небольших интервалов между шагами расчета, когда предел Найквиста велик по сравнению с пропускной способностью регулятора. При больших временах дискретизации метод
Forward Eulerможет привести к нестабильности, даже в случае дискретизации системы, стабильной в непрерывном времени. -
Backward Euler— обратная прямоугольная (правая) аппроксимация:.
Преимущество метода
Backward Eulerсостоит в том, что дискретизация устойчивой системы с непрерывным временем с использованием этого метода всегда дает устойчивый результат с дискретным временем. -
Trapezoidal— билинейное приближение:.
Преимущество метода
Trapezoidalсостоит в том, что дискретизация устойчивой системы с непрерывным временем с использованием этого метода всегда дает устойчивый результат с дискретным временем. Из всех доступных методов интегрирования методTrapezoidalдает наиболее близкое соответствие между свойствами частотной области дискретизированной системы и соответствующей системы с непрерывным временем.
Зависимости
Чтобы использовать этот параметр, установите для Time domain значение Discrete-time.
| Значения |
|
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Нет |
#
Filter method —
метод вычисления производной в дискретном регуляторе
Forward Euler | Backward Euler | Trapezoidal
Details
В дискретном времени дифференциальный член передаточной функции регулятора равен:
,
где зависит от метода интегрирования:
-
Forward Euler— прямая прямоугольная (левая) аппроксимация:.
Этот метод лучше всего подходит для небольших интервалов между шагами расчета, когда предел Найквиста велик по сравнению с пропускной способностью регулятора. При больших временах дискретизации метод
Forward Eulerможет привести к нестабильности, даже в случае дискретизации системы, стабильной в непрерывном времени. -
Backward Euler— обратная прямоугольная (правая) аппроксимация:.
Преимущество метода
Backward Eulerсостоит в том, что дискретизация устойчивой системы с непрерывным временем с использованием этого метода всегда дает устойчивый результат с дискретным временем. -
Trapezoidal— билинейное приближение:.
Преимущество метода
Trapezoidalсостоит в том, что дискретизация устойчивой системы с непрерывным временем с использованием этого метода всегда дает устойчивый результат с дискретным временем. Из всех доступных методов интегрирования методTrapezoidalдает наиболее близкое соответствие между свойствами частотной области дискретизированной системы и соответствующей системы с непрерывным временем.
Зависимости
Чтобы использовать этот параметр, установите для Time domain значение Discrete-time.
| Значения |
|
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Нет |
Параметры
#
Differentiator initial condition —
начальное значение производной
Real number
Details
Начальное значение производной.
Зависимости
Чтобы использовать этот параметр, установите для Time domain значение Discrete-time, снимите флажок Use filtered derivative, а для параметра Controller установите значение PID, PD.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |
#
Filter initial condition —
начальное значение фильтра
Real number
Details
Начальное значение фильтра.
Зависимости
Чтобы использовать этот параметр, установите для Time domain значение Discrete-time, установите флажок Use filtered derivative, а для параметра Controller установите значение PID, PD.
Или установите для Time domain значение Continuous-time, а для параметра Controller установите значение PID, PD.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |
#
Integrator initial condition —
начальное значение интегратора
Real number
Details
Начальное значение интегратора.
Зависимости
Чтобы использовать этот параметр, установите для параметра Controller значение PID, PI или I.
| Значение по умолчанию |
|
| Имя для программного использования |
|
| Настраиваемый |
Нет |
| Вычисляемый |
Да |

