Что такое системное моделирование
В этой статье мы рассмотрим концепции и термины, которые используются в среде Engee.
Система
Система — группа взаимозависимых физических и функциональных частей, характеристики которых, во-первых, измеримы, а во-вторых, изменяются во времени.
Например, автомобиль можно рассмотреть как систему, состоящую из нескольких частей. Примеры характеристик — линейная скорость и скорость вращения колес.

Системный компонент
Системный компонент — это часть системы, которая взаимодействует с другими частями. Взаимодействия между компонентами определяют структуру и поведение системы.
Например, модуль круиз-контроля является системным компонентом в системе автомобиля. Микроконтроллер и связанное с ним оборудование определяют структуру, а программный алгоритм управления скоростью определяет поведение.

Модель
Модель — это математическое описание системы, полученное либо из физических законов, либо из экспериментальных данных. В модели, как правило, используется набор переменных, связанных дифференциальными и алгебраическими уравнениями, и коэффициенты этих уравнений.
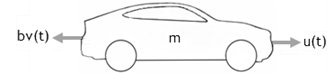
Вернемся к упрощенной модели автомобиля.
Переменные:
-
u(t)— сила (Н), действующая на автомобиль; -
v(t)— скорость автомобиля (м/с). Параметры: -
b— коэффициент лобового сопротивления (Н·с/м); -
m— масса (кг).
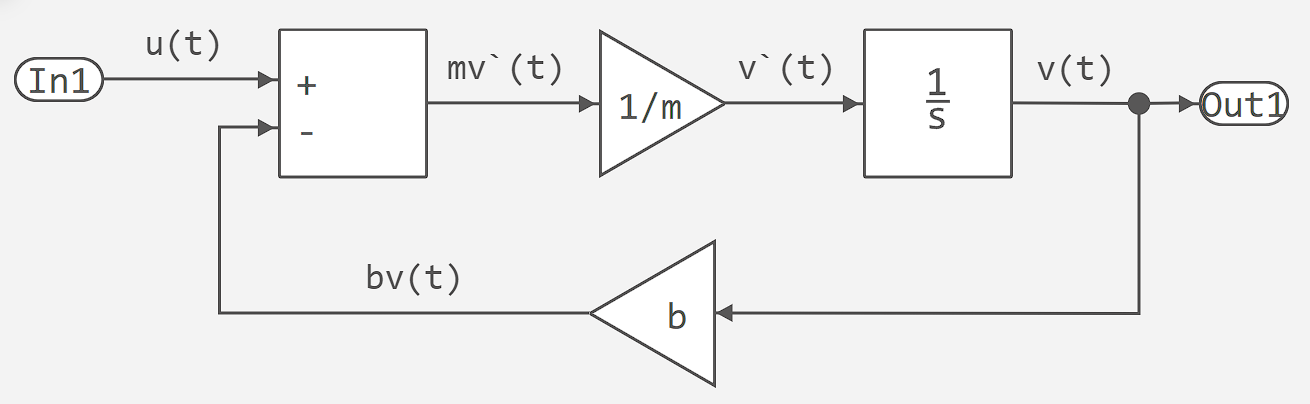
Представим автомобиль как непрерывную систему. Тогда изменения всех переменных могут быть полностью описаны с помощью системы дифференциальных уравнений, определенных для всех значений времени. Скорость транспортного средства v(t) и его ускорение v'(t) связаны следующим дифференциальным уравнением первого порядка.
Можно создать модель Engee для этого уравнения. Для этого нужно перенести в модель соответствующие блоки, задать их параметры и, используя сигнальные линии, соединить их друг с другом. Следующая блок-схема Engee реализует указанное дифференциальное уравнение:
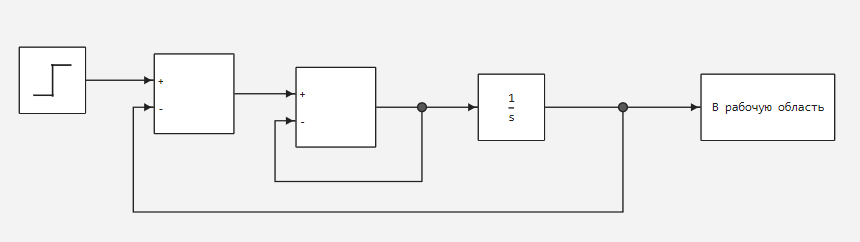
Дифференциально-алгебраические уравнения
Некоторые системы уравнений содержат дополнительные ограничения, которые включают независимую переменную и вектор состояния в дополнение к дифференциальным уравнениям. Такие системы называются дифференциально-алгебраическими уравнениями (ДАУ).
Термин алгебраический относится к уравнениям, которые не содержат производных.
В моделях Engee алгебраические циклы, или петли, являются алгебраическими ограничениями. Модели с алгебраическими петлями определяют систему дифференциально-алгебраических уравнений.
Например,
представляет систему дифференциально-алгебраических уравнений, реализованную в следующей модели Engee: