Краткий обзор нейронной сети
Если вы уже использовали нейронные сети, то этот простой пример может помочь понять взаимодействие основных частей Flux. Попробуйте вставить код в строку REPL.
Если это не вариант, возможно, вас больше заинтересует эта страница.
# Появится запрос на установку всего необходимого, включая CUDA:
using Flux, CUDA, Statistics, ProgressMeter
# Сгенерируем данные для задачи XOR: векторы длиной 2 в виде столбцов матрицы:
noisy = rand(Float32, 2, 1000) # матрица 2×1000 {Float32}
truth = [xor(col[1]>0.5, col[2]>0.5) for col in eachcol(noisy)] # 1000-элементный вектор {Bool}
# Определим модель — многослойный перцептрон с одним скрытым слоем размером 3:
model = Chain(
Dense(2 => 3, tanh), # функция активации внутри слоя
BatchNorm(3),
Dense(3 => 2),
softmax) |> gpu # переместим модель в GPU, если GPU доступен
# Модель инкапсулирует параметры, инициализируемые случайным образом. Начальный вывод выглядит следующим образом:
out1 = model(noisy |> gpu) |> cpu # матрица 2×1000 {Float32}
# Для обучения модели мы используем пакеты из 64 образцов и кодирование с одним активным состоянием:
target = Flux.onehotbatch(truth, [true, false]) # OneHotMatrix размером 2×1000
loader = Flux.DataLoader((noisy, target) |> gpu, batchsize=64, shuffle=true);
# 16-элементный DataLoader с первым элементом: (2×64 Matrix{Float32}, 2×64 OneHotMatrix)
optim = Flux.setup(Flux.Adam(0.01), model) # будет хранить импульсы оптимизатора и т. д.
# Цикл обучения, использующий весь набор данных 1000 раз:
losses = []
@showprogress for epoch in 1:1_000
for (x, y) in loader
loss, grads = Flux.withgradient(model) do m
# Оценим модель и потери в контексте градиента:
y_hat = m(x)
Flux.crossentropy(y_hat, y)
end
Flux.update!(optim, model, grads[1])
push!(losses, loss) # регистрация в журнале, вне контекста градиента
end
end
optim # параметры, моменты и вывод изменились
out2 = model(noisy |> gpu) |> cpu # первая строка — вероятность true, вторая — вероятность false
mean((out2[1,:] .> 0.5) .== truth) # на данный момент точность 94 %!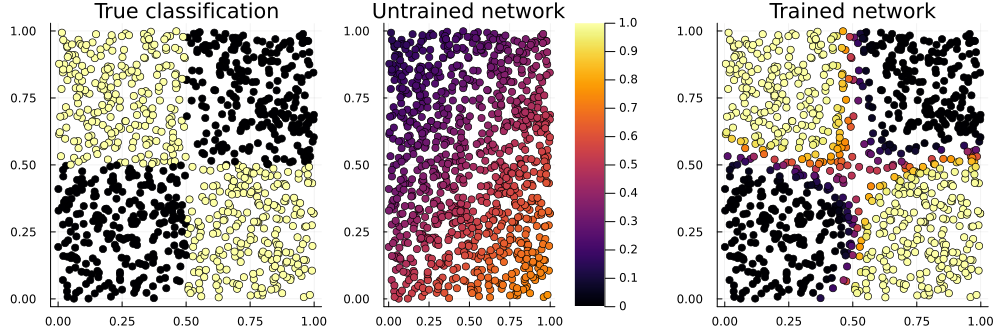
using Plots # чтобы нарисовать приведенный выше рисунок
p_true = scatter(noisy[1,:], noisy[2,:], zcolor=truth, title="True classification", legend=false)
p_raw = scatter(noisy[1,:], noisy[2,:], zcolor=out1[1,:], title="Untrained network", label="", clims=(0,1))
p_done = scatter(noisy[1,:], noisy[2,:], zcolor=out2[1,:], title="Trained network", legend=false)
plot(p_true, p_raw, p_done, layout=(1,3), size=(1000,330))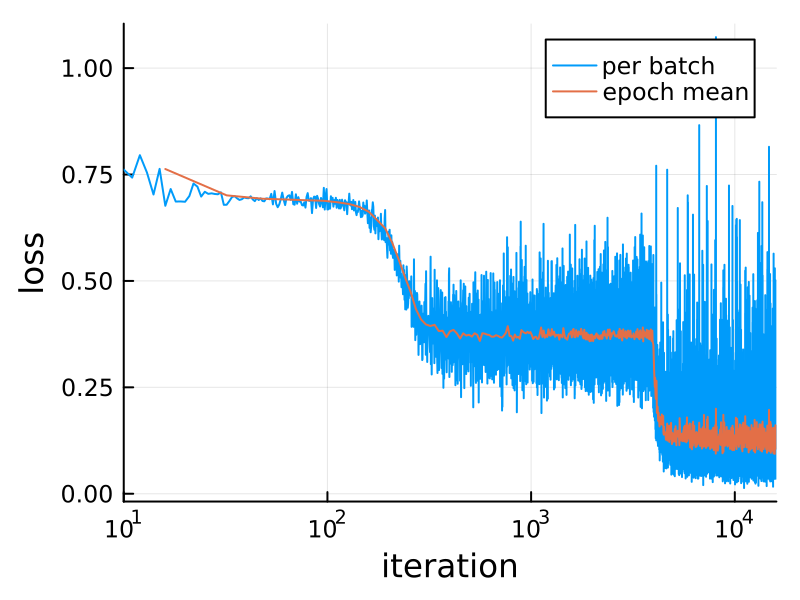
Вот потеря во время обучения:
plot(losses; xaxis=(:log10, "iteration"),
yaxis="loss", label="per batch")
n = length(loader)
plot!(n:n:length(losses), mean.(Iterators.partition(losses, n)),
label="epoch mean", dpi=200)Эта задача XOR («исключающее ИЛИ») является вариантом знаменитой задачи, которая в 1969 году подтолкнула Минского и Паперта к изобретению глубоких нейронных сетей. При малых значениях «глубины» существует один скрытый слой, в то время как в ранних перцептронах не было ни одного. (То, что они называют скрытым слоем, во Flux называется выводом первого слоя model[1](noisy).)
С тех пор ситуация несколько изменилась.
Особенности, на которые стоит обратить внимание
В этом примере следует обратить внимание на следующие моменты.
-
Пакетное измерение данных всегда является последним. Таким образом,
2×1000 Matrixпредставляет собой тысячу наблюдений, каждое из которых имеет вид столбца длиной 2. Во Flux по умолчанию используетсяFloat32, но в большей части Julia —Float64. -
modelможно вызывать как функциюy = model(x). Каждый слой типаDenseпредставляет собой обычныйstruct, который инкапсулирует некоторые массивы параметров (и, возможно, другие состояния, как в случае сBatchNorm). -
Но модель не содержит ни функции потерь, ни правила оптимизации. Импульсы, необходимые для
Adam, хранятся в объекте, возвращаемомFlux.Train.setup. АFlux.crossentropyявляется обычной функцией. -
Блок
doсоздает анонимную функцию в качестве первого аргументаgradient. Все, что выполняется в этих рамках, является дифференцированным.
Вместо того чтобы вызывать gradient и update! по отдельности, можно воспользоваться вспомогательной функцией train!. Если не нужно выполнять дополнительные задачи (например, регистрировать потери в журнале), можно заменить цикл обучения следующим:
for epoch in 1:1_000
Flux.train!(model, loader, optim) do m, x, y
y_hat = m(x)
Flux.crossentropy(y_hat, y)
end
end|
Совместимость: Implicit-style training, Flux ≤ 0.14
До недавнего времени обучение Flux проходило немного по-другому. Любой код следующего вида (градиент функции с нулевым аргументом) или (с |