Рекуррентные модели

Рекуррентные ячейки

Чтобы представить рекуррентные функции Flux, рассмотрим следующую структуру простой рекуррентной нейронной сети.

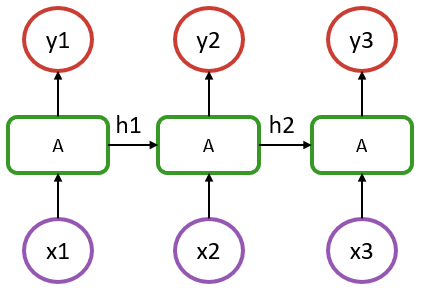
В приведенном выше примере есть последовательность длиной 3, где x1--x3 представляют входные данные на каждом шаге (это может быть временная метка или слово в предложении), а y1--y3 их соответствующие выходные данные.

Следует отметить, что в такой модели рекуррентные ячейки A относятся к одной и той же структуре. От простого плотного слоя ее отличает то, что в ячейку A, помимо входного значения x, поступает информация из предыдущего состояния модели (скрытое состояние обозначено на схеме как h1 и h2).

В самом базовом случае RNN ячейка A может быть определена следующим образом:

output_size = 5
input_size = 2
Wxh = randn(Float32, output_size, input_size)
Whh = randn(Float32, output_size, output_size)
b   = randn(Float32, output_size)

function rnn_cell(h, x)
    h = tanh.(Wxh * x .+ Whh * h .+ b)
    return h, h
end

x = rand(Float32, input_size) # фиктивные входные данные
h = rand(Float32, output_size) # случайное начальное скрытое состояние

h, y = rnn_cell(h, x)

Обратите внимание, что выше, по сути, указан слой Dense, который использует два входных значения — h и x.

Если вы выполните последнюю строку несколько раз, вы заметите, что выходное значение y немного изменилось, хотя входное значение x осталось прежним.

Во Flux доступны различные рекуррентные ячейки, в частности RNNCell, LSTMCell и GRUCell, которые описаны в справке по слоям. Приведенный выше рукописный пример можно заменить следующим:

using Flux

rnn = Flux.RNNCell(2, 5)

x = rand(Float32, 2) # фиктивные данные
h = rand(Float32, 5)  # начальное скрытое состояние

h, y = rnn(h, x)

Модели с сохранением состояния

По большей части мы не хотим самостоятельно управлять скрытыми состояниями, но хотим считать модели как сохраняющие состояние. Для этого во Flux есть оболочка Recur.

x = rand(Float32, 2)
h = rand(Float32, 5)

m = Flux.Recur(rnn, h)

y = m(x)

Оболочка Recur хранит состояние между запусками в поле m.state.

Если используется конструктор RNN(2, 5), а не RNNCell, вы увидите, что это просто заключенная в оболочку ячейка.

julia> using Flux

julia> RNN(2, 5)  # или эквивалентно RNN(2 => 5)
Recur(
  RNNCell(2 => 5, tanh),                # 45 параметров
)         # Всего: 4 обучаемых массива, 45 параметров,
          # плюс 1 необучаемый, 5 параметров, суммарный размер 412 байт.

Эквивалентен конструктору RNN с сохранением состояния. Также доступны LSTM и GRU.

Используя эти инструменты, можно построить модель, показанную на схеме выше, следующим образом:

julia> m = Chain(RNN(2 => 5), Dense(5 => 1))
Chain(
  Recur(
    RNNCell(2 => 5, tanh),              # 45 параметров
  ),
  Dense(5 => 1),                        # 6 параметров
)         # Всего: 6 обучаемых массивов, 51 параметр,
          # плюс 1 необучаемый, 5 параметров, суммарный размер 580 байт.

В этом примере каждый вывод имеет только один компонент.

Работа с последовательностями

Используя ранее определенную рекуррентную модель m, мы можем теперь применить ее к одному шагу из последовательности:

julia> x = rand(Float32, 2);

julia> m(x)
1-element Vector{Float32}:
 0.45860028

Операция m(x) будет представлена на диаграмме в виде x1 -> A -> y1. Если выполнить эту операцию во второй раз, она будет эквивалентна x2 -> A -> y2, поскольку модель m сохранила состояние, полученное в результате шага x1.

Теперь, вместо того чтобы вычислять один шаг за раз, можно получить полную последовательность y1--y3 за один проход, итерируя модель по последовательности данных.

Для этого нужно структурировать входные данные как вектор (Vector) наблюдений на каждом временном шаге. Таким образом, этот вектор (Vector) будет иметь длину length = seq_length, и каждый его элемент будет представлять входные признаки для заданного шага. В нашем примере это означает вектор (Vector) длиной 3, где каждый элемент представляет собой матрицу (Matrix) размером (features, batch_size), или просто вектор (Vector) длины features, если речь идет об одном наблюдении.

julia> x = [rand(Float32, 2) for i = 1:3];

julia> [m(xi) for xi in x]
3-element Vector{Vector{Float32}}:
 [0.36080405]
 [-0.13914406]
 [0.9310162]

Не рекомендуется использовать операции сопоставления и трансляции со слоями с сохранением состояния, так как язык Julia не гарантирует определенного порядка выполнения. Поэтому не используйте

y = m.(x)
# или
y = map(m, x)

а применяйте явные циклы

y = [m(x) for x in x]

If for some reason one wants to exclude the first step of the RNN chain for the computation of the loss, that can be handled with:

using Flux.Losses: mse

function loss(x, y)
  m(x[1]) # игнорирует вывод, но обновляет скрытые состояния. Если по какой-то причине вы хотите исключить первый шаг цепочки RNN для вычисления потерь, это можно сделать следующим образом.
  sum(mse(m(xi), yi) for (xi, yi) in zip(x[2:end], y))
end

y = [rand(Float32, 1) for i=1:2]
loss(x, y)

В такой модели для вычисления потерь используются только два последних вывода, поэтому целевой y имеет длину 2. С помощью этой стратегии можно легко работать со структурой типа seq-to-one, в отличие от seq-to-seq, которая предполагалась ранее.

Или же если необходимо подготовить последовательность к работе, ее можно выполнить один раз, а затем провести обычное обучение, в котором все шаги последовательности будут учитываться для обновления градиента:

function loss(x, y)
  sum(mse(m(xi), yi) for (xi, yi) in zip(x, y))
end

seq_init = [rand(Float32, 2)]
seq_1 = [rand(Float32, 2) for i = 1:3]
seq_2 = [rand(Float32, 2) for i = 1:3]

y1 = [rand(Float32, 1) for i = 1:3]
y2 = [rand(Float32, 1) for i = 1:3]

X = [seq_1, seq_2]
Y = [y1, y2]
data = zip(X,Y)

Flux.reset!(m)
[m(x) for x in seq_init]

ps = Flux.params(m)
opt= Adam(1e-3)
Flux.train!(loss, ps, data, opt)

В предыдущем примере состояние модели сначала сбрасывается с помощью Flux.reset!. Затем происходит разогрев (warmup), который выполняется для последовательности длиной 1 путем подачи в нее seq_init, что приводит к состоянию разогрева. Модель может быть обучена в течение одной эпохи, когда предоставляются два пакета (seq_1 и seq_2) и все выводы временных интервалов учитываются при определении потери.

В этом сценарии важно отметить, что рассматривается одна непрерывная последовательность. Поскольку состояние модели не сбрасывается между двумя пакетами, состояние модели передается через пакеты, что имеет смысл только в контексте, когда seq_1 является продолжением seq_init и так далее.

Размер пакета здесь будет равен 1, поскольку в каждом пакете есть только одна последовательность. Если модель должна быть обучена на основе нескольких независимых последовательностей, эти последовательности можно добавить к входным данным в качестве второго измерения. Например, в языковой модели каждый пакет будет содержать несколько независимых предложений. Если в таком сценарии задать размер партии равным 4, один пакет будет иметь следующую форму:

x = [rand(Float32, 2, 4) for i = 1:3]
y = [rand(Float32, 1, 4) for i = 1:3]

Это означает, что у нас есть четыре предложения (или образца), каждое с двумя признаками (допустим, очень маленькое вложение) и каждое длиной 3 (три слова в предложении). Вычисление m(batch[1]) по-прежнему представляет x1 -> y1 на схеме и возвращает вывод первого слова, но теперь для каждого из четырех независимых предложений (второе измерение входной матрицы). Здесь не нужно использовать Flux.reset!(m). Каждое предложение в пакете будет выводиться в своем собственном «столбце», и выводы разных предложений не будут смешиваться.

Чтобы проиллюстрировать этот случай, рассмотрим пример пакетной обработки в нашей реализации rnn_cell. Реализацию изменять не нужно. Пакетная обработка выполняется «бесплатно» на основе способа осуществления трансляции и правил умножения матриц в Julia.

output_size = 5
input_size = 2
Wxh = randn(Float32, output_size, input_size)
Whh = randn(Float32, output_size, output_size)
b   = randn(Float32, output_size)

function rnn_cell(h, x)
    h = tanh.(Wxh * x .+ Whh * h .+ b)
    return h, h
end

Здесь мы используем последнее измерение входных данных и скрытое состояние в качестве измерения пакета. То есть h[:, n] будет скрытым состоянием n-го предложения в пакете.

batch_size = 4
x = rand(Float32, input_size, batch_size) # фиктивные входные данные
h = rand(Float32, output_size, batch_size) # случайное начальное скрытое состояние

h, y = rnn_cell(h, x)

julia> size(h) == size(y) == (output_size, batch_size)
true

Во многих ситуациях, например при работе с языковой моделью, предложения в каждом пакете являются независимыми (то есть последний элемент первого предложения первого пакета не зависит от первого элемента первого предложения второго пакета), поэтому мы не можем работать с моделью так, как если бы каждый пакет был прямым продолжением предыдущего. В таких случаях необходимо сбрасывать состояние модели между каждым пакетом, что можно удобно сделать в функции потерь:

function loss(x, y)
  Flux.reset!(m)
  sum(mse(m(xi), yi) for (xi, yi) in zip(x, y))
end

Потенциальным источником неоднозначности при использовании RNN во Flux может быть другая структура данных, если рассматривать некоторые распространенные платформы, где данные обычно представляют собой трехмерный массив: (features, seq length, samples). Во Flux эти три измерения предоставляются через вектор длины последовательностей, содержащий матрицу (features, samples).