Документация Engee

Управление алгоритмом интерполяции

B-сплайны

Тип интерполяции описывается степенью и при необходимости граничными условиями. В настоящее время доступны четыре степени: Constant, Linear, Quadratic и Cubic. Они соответствуют B-сплайнам степени 0, 1, 2 и 3.

B-сплайны квадратной или более высокой степени требуют решения системы уравнений для получения интерполяционных коэффициентов. Для этого необходимо указать граничное условие, применяемое для замыкания системы. Реализованы следующие граничные условия: Flat, Line (либо Natural), Free, Periodic и Reflect; их математический смысл подробно описывается в соответствующих docstring. При указании этих граничных условий необходимо также указать, применяются ли они в крайней точке сетки (OnGrid()) или за ней на середине интервала до следующей (мнимой) точки сетки (OnCell()).

Некоторые примеры:

# Интерполяция по алгоритму ближайшего соседа
itp = interpolate(a, BSpline(Constant()))
v = itp(5.4)   # возвращает a[5]

# Интерполяция по алгоритму предыдущего соседа
itp = interpolate(a, BSpline(Constant(Previous)))
v = itp(1.8)   # возвращает a[1]

# Интерполяция по алгоритму следующего соседа
itp = interpolate(a, BSpline(Constant(Next)))
v = itp(5.4)   # возвращает a[6]

# (Поли)линейная интерполяция
itp = interpolate(A, BSpline(Linear()))
v = itp(3.2, 4.1)  # возвращает 0.9*(0.8*A[3,4]+0.2*A[4,4]) + 0.1*(0.8*A[3,5]+0.2*A[4,5])

# Квадратичная интерполяция с отражательными граничными условиями
# Квадратный порядок — это наименьший порядок с непрерывным градиентом
itp = interpolate(A, BSpline(Quadratic(Reflect(OnCell()))))

# Линейная интерполяция в первом измерении и отсутствие интерполяции (только поиск) во втором
itp = interpolate(A, (BSpline(Linear()), NoInterp()))
v = itp(3.65, 5)  # возвращает 0.35*A[3,5] + 0.65*A[4,5]

Доступны и другие варианты, например:

# Интерполяция на месте
itp = interpolate!(A, BSpline(Quadratic(InPlace(OnCell()))))

Входной массив A при этом уничтожается, но выделяется меньше памяти.

Масштабированные B-сплайны

B-сплайны предполагают равномерное распределение данных на сетке 1:N или ее многомерном эквиваленте. Если данные имеют форму [f(x) for x in A], пакету Interpolations необходимо сообщить информацию о сетке A. Если A имеет неравномерное распределение, следует использовать описанную ниже сеточную интерполяцию. Однако если A — это коллекция диапазонов или linspace, можно использовать масштабированные B-сплайны. Такой подход эффективнее, так как сеточный алгоритм не использует равномерное распределение. Кроме того, масштабированные B-сплайны можно использовать с любой степенью, доступной для B-сплайнов, в то время как сеточная интерполяция в настоящее время не поддерживает квадратические или кубические сплайны.

Вот несколько примеров:

A_x = 1.:2.:40.
A = [log(x) for x in A_x]
itp = interpolate(A, BSpline(Cubic(Line(OnGrid()))))
sitp = scale(itp, A_x)
sitp(3.) # ровно log(3.)
sitp(3.5) # примерно log(3.5)

Для многомерных сеток с равномерным распределением

A_x1 = 1:.1:10
A_x2 = 1:.5:20
f(x1, x2) = log(x1+x2)
A = [f(x1,x2) for x1 in A_x1, x2 in A_x2]
itp = interpolate(A, BSpline(Cubic(Line(OnGrid()))))
sitp = scale(itp, A_x1, A_x2)
sitp(5., 10.) # ровно log(5 + 10)
sitp(5.6, 7.1) # примерно log(5.6 + 7.1)

Сеточная интерполяция

Синтаксис этих методов очень похож на синтаксис B-сплайнов. Основное отличие в том, что не нужно выбирать представление сетки (всегда используется OnGrid). Достаточно указать множество массивов координат, определяющих узлы массива.

Для одного измерения:

A = rand(20)
A_x = 1.0:2.0:40.0
nodes = (A_x,)
itp = interpolate(nodes, A, Gridded(Linear()))
itp(2.0)

Интервалы между соседними выборками не обязательно должны быть постоянными; на самом деле, если они постоянные, более производительным будет метод scaled.

В общем виде синтаксис выглядит так:

itp = interpolate(nodes, A, options...)

где nodes = (xnodes, ynodes, ...) — это позиции на каждой оси, по которой из массива A производится произвольная («прямоугольная») выборка.

Например:

A = rand(8,20)
nodes = ([x^2 for x = 1:8], [0.2y for y = 1:20])
itp = interpolate(nodes, A, Gridded(Linear()))
itp(4,1.2)  # примерно A[2,6]

Режимы можно сочетать друг с другом, явно указывая вектор режимов в виде кортежа:

itp = interpolate(nodes, A, (Gridded(Linear()),Gridded(Constant())))

В настоящее время существует всего три режима сеточной интерполяции:

Gridded(Linear())

при котором между узлами применяется линейная интерполяция;

Gridded(Constant())

при котором к соответствующей оси применяется интерполяция по алгоритму ближайшего соседа;

NoInterp()

при котором координата выбранного входного вектора ДОЛЖНА находиться в точке сетки. Если запрашиваются координаты за пределами сетки, выдается ошибка.

Для Constant есть дополнительные параметры. Используйте Constant{Previous}() для выполнения интерполяции по алгоритму предыдущего соседа. Используйте Constant{Next}() для выполнения интерполяции по алгоритму следующего соседа. Имейте в виду, что округление может вызывать проблемы. См. описание проблемы № 473.

Данные со значением missing естественным образом распространяются при интерполяции, из-за чего некоторые значения могут отсутствовать. Чтобы избежать этого, можно отфильтровать отсутствующие точки данных и использовать сеточную интерполяцию. Например:

x = 1:6
A = [i == 3 ? missing : i for i in x]
xf = [xi for (xi,a) in zip(x, A) if !ismissing(a)]
Af = [a for a in A if !ismissing(a)]
itp = interpolate((xf, ), Af, Gridded(Linear()))

Возможна также сеточная интерполяция на месте:

x = 1:4
y = view(rand(4), :)
itp = interpolate!((x,), y, Gridded(Linear()))
y .= 0
@show itp(2.5) # 0

Параметрические сплайны

Для данного множества узлов с координатами x(t) и y(t) можно создать параметрический сплайн S(t) = (x(t),y(t)), параметризованный по t in [0,1], с помощью следующего кода, за основу которого взят код из публикации Томаса Ликена (Tomas Lycken):

using Interpolations

t = 0:.1:1
x = sin.(2π*t)
y = cos.(2π*t)
A = hcat(x,y)

itp = Interpolations.scale(interpolate(A, (BSpline(Cubic(Natural(OnGrid()))), NoInterp())), t, 1:2)

tfine = 0:.01:1
xs, ys = [itp(t,1) for t in tfine], [itp(t,2) for t in tfine]

Затем можно построить график сплайна следующим образом:

using Plots

scatter(x, y, label="knots")
plot!(xs, ys, label="spline")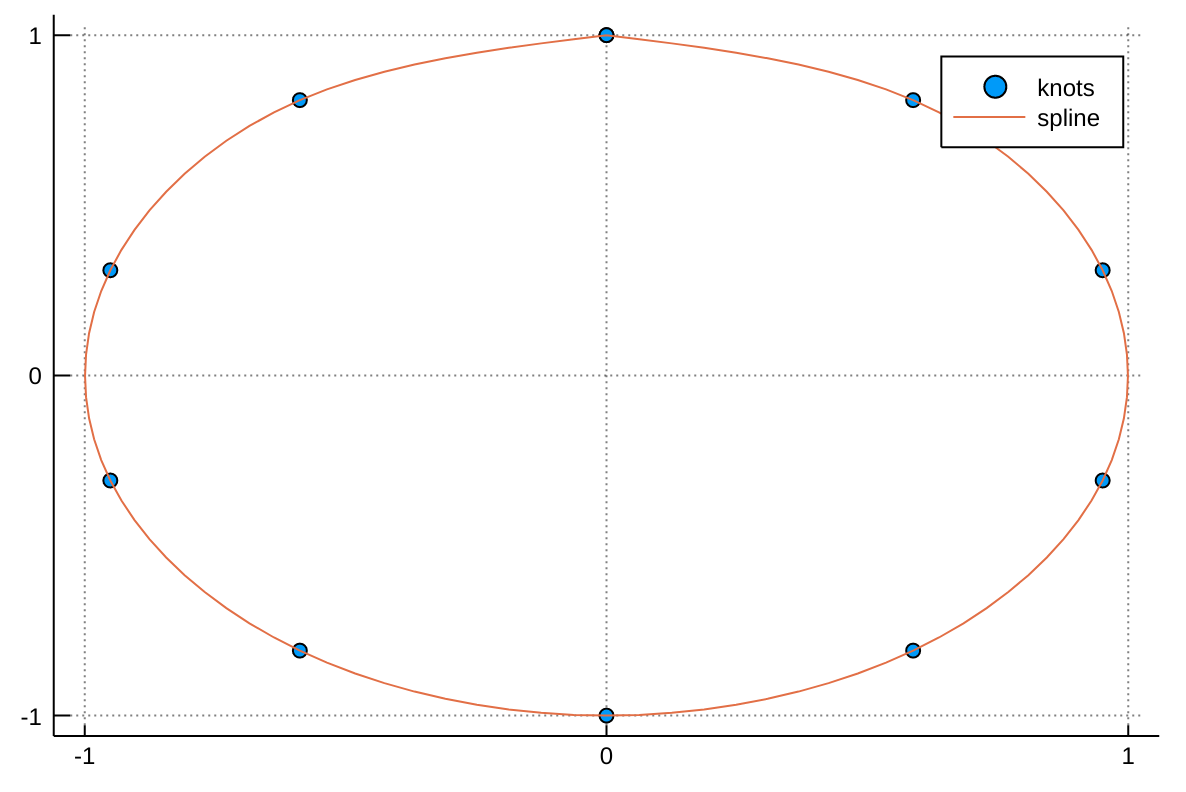
параметрический сплайн

Монотонная интерполяция

Для некоторых одномерных монотонных данных многие стандартные методы интерполяции могут давать интерполяционную функцию, не являющуюся монотонной. Монотонная интерполяция гарантирует монотонность интерполяционной функции.

Вот пример построения интегральной функции распределения для некоторых данных:

percentile_values = [0.0, 0.01, 0.1, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 91.0, 92.0, 93.0, 94.0, 95.0, 96.0, 97.0, 98.0, 99.0, 99.9, 99.99, 100.0];

y = sort(randn(length(percentile_values))); # некоторые случайные данные

itp_cdf = extrapolate(interpolate(y, percentile_values, SteffenMonotonicInterpolation()), Flat());

t = -3.0:0.01:3.0 # просто диапазон для вычисления значений интерполяционной функции

interpolated_cdf = map(itp_cdf, t) # интерполяция интегральной функции распределения

Существует несколько разных алгоритмов монотонной интерполяции. Некоторые из них гарантируют, что для немонотонных данных интерполяционная функция не выходит за пределы диапазона значений между двумя следующими друг за другом точками, в то время как другие — нет (в списке ниже это называется выбросом).

Узнать больше о монотонной интерполяции можно в следующих материалах:

  • Фритч (Fritsch) и Карлсон (Carlson) (1980), Monotone Piecewise Cubic Interpolation, doi: 10.1137/0717021.

  • Фритч (Fritsch) и Бутленд (Butland) (1984), A Method for Constructing Local Monotone Piecewise Cubic Interpolants, doi: 10.1137/0905021.

  • Стеффен (Steffen) (1990), A Simple Method for Monotonic Interpolation in One Dimension, URL