Удобная нотация
Наглядный пример
Удобный конструктор позволяет упрощать выражения. Например, создание объекта интерполяции
extrap_full = extrapolate(scale(interpolate(A, BSpline(Linear())), xs), Line())можно записать в более удобочитаемом виде
extrap = linear_interpolation(xs, A, extrapolation_bc = Line())с помощью удобного конструктора.
Использование
f(x) = log(x)
xs = 1:0.2:5
A = [f(x) for x in xs]
# линейная интерполяция
interp_linear = linear_interpolation(xs, A)
interp_linear(3) # ровно log(3)
interp_linear(3.1) # примерно log(3.1)
# интерполяция кубическими сплайнами
interp_cubic = cubic_spline_interpolation(xs, A)
interp_cubic(3) # ровно log(3)
interp_cubic(3.1) # примерно log(3.1)Также поддерживаются многомерные данные:
f(x,y) = log(x+y)
xs = 1:0.2:5
ys = 2:0.1:5
A = [f(x,y) for x in xs, y in ys]
# линейная интерполяция
interp_linear = linear_interpolation((xs, ys), A)
interp_linear(3, 2) # ровно log(3 + 2)
interp_linear(3.1, 2.1) # примерно log(3.1 + 2.1)
# интерполяция кубическими сплайнами
interp_cubic = cubic_spline_interpolation((xs, ys), A)
interp_cubic(3, 2) # ровно log(3 + 2)
interp_cubic(3.1, 2.1) # примерно log(3.1 + 2.1)В случае с экстраполяцией, то есть когда объекты интерполяции вычисляются в координатах за пределами указанного в конструкторе диапазона, граничным условием по умолчанию является Throw, так что возвращается ошибка. При необходимости граничные условия можно указать с помощью дополнительного параметра extrapolation_bc:
f(x) = log(x)
xs = 1:0.2:5
A = [f(x) for x in xs]
# экстраполяция с линейными граничными условиями
extrap = linear_interpolation(xs, A, extrapolation_bc = Line())
@test extrap(1 - 0.2) # ≈ f(1) - (f(1.2) - f(1))
@test extrap(5 + 0.2) # ≈ f(5) + (f(5) - f(4.8))Вы также можете использовать «значение-заполнитель», которое возвращается при запросе значений за пределами диапазона:
extrap = linear_interpolation(xs, A, extrapolation_bc = NaN)
@test isnan(extrap(5.2))Кроме того, поддерживаются нерегулярные сетки, но в настоящее время только методами constant_interpolation и linear_interpolation.
xs = [x^2 for x = 1:0.2:5]
A = [f(x) for x in xs]
# линейная интерполяция
interp_linear = linear_interpolation(xs, A)
interp_linear(1) # ровно log(1)
interp_linear(1.05) # примерно log(1.05)Пример с Plots.jl
Интерполированный объект можно легко построить на графике с помощью пакета Plots.jl. Вот простой пример:
using Interpolations, Plots
# Нижняя и верхняя границы интервала
a = 1.0
b = 10.0
# Определение интервала
x = a:1.0:b
# Это может быть любой массив данных при условии, что
# length(x) == length(y)
y = @. cos(x^2 / 9.0) # Применение функции путем трансляции
# Интерполяции
itp_linear = linear_interpolation(x, y)
itp_cubic = cubic_spline_interpolation(x, y)
# Интерполяционные функции
f_linear(x) = itp_linear(x)
f_cubic(x) = itp_cubic(x)
# Графики
width, height = 1500, 800 # не строго обязательно
x_new = a:0.1:b # более плавный интервал, необходимый для кубического сплайна
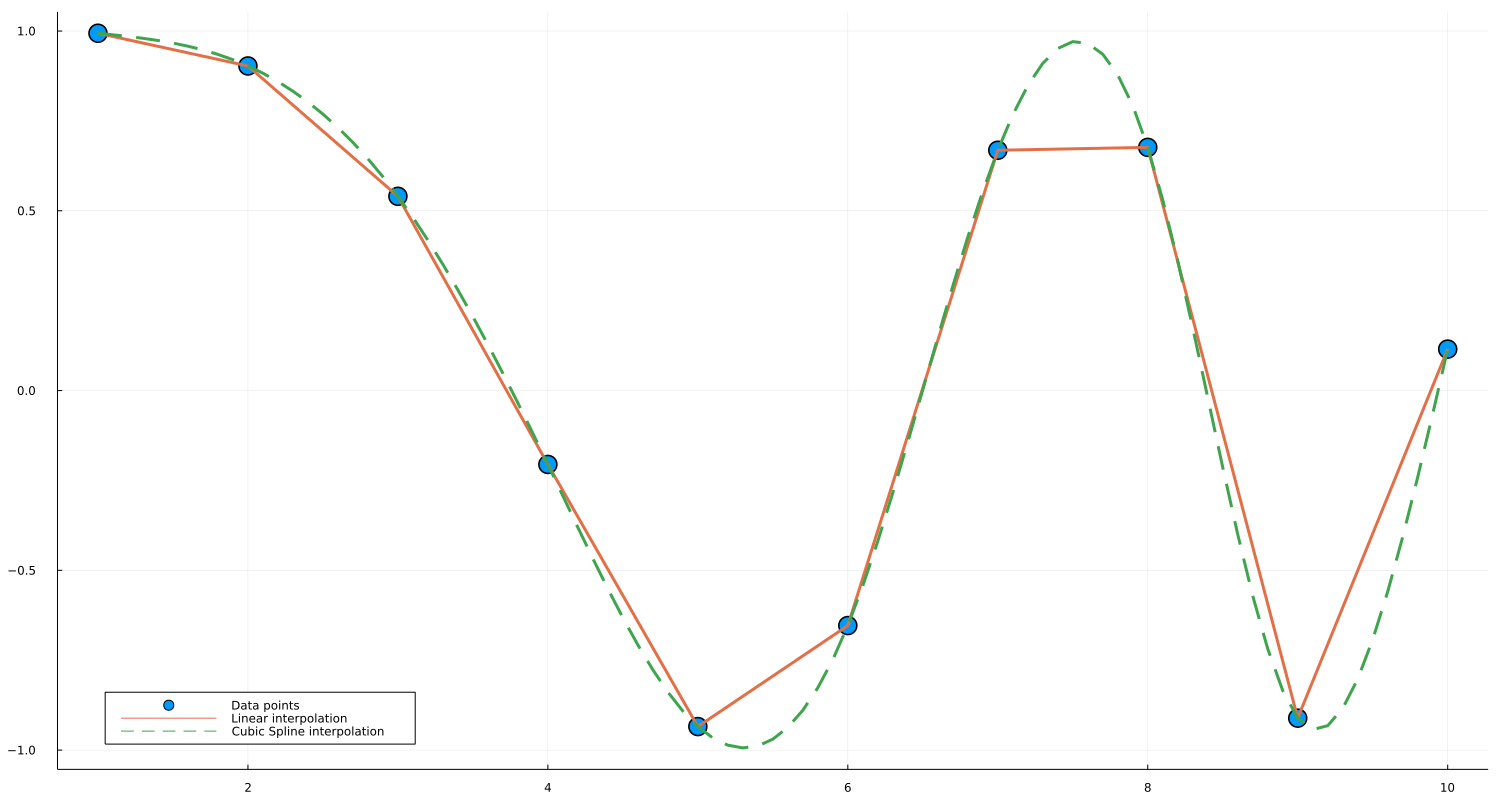
scatter(x, y, markersize=10,label="Data points")
plot!(f_linear, x_new, w=3,label="Linear interpolation")
plot!(f_cubic, x_new, linestyle=:dash, w=3, label="Cubic Spline interpolation")
plot!(size = (width, height))
plot!(legend = :bottomleft)Сгенерированный график имеет следующий вид: