Судоку
Это руководство было изначально предоставлено Иэном Даннингом (Iain Dunning).
Судоку — это популярная числовая головоломка. Цель состоит в том, чтобы вписать цифры от 1 до 9 в сетку размером девять на девять, при этом некоторые цифры уже заполнены. Решение должно удовлетворять следующим правилам:
-
В каждом квадрате 3x3 должны быть все цифры от 1 до 9.
-
В каждой строке должны быть все цифры от 1 до 9.
-
В каждом столбце должны быть все цифры от 1 до 9.
Вот частично решенная задача судоку:
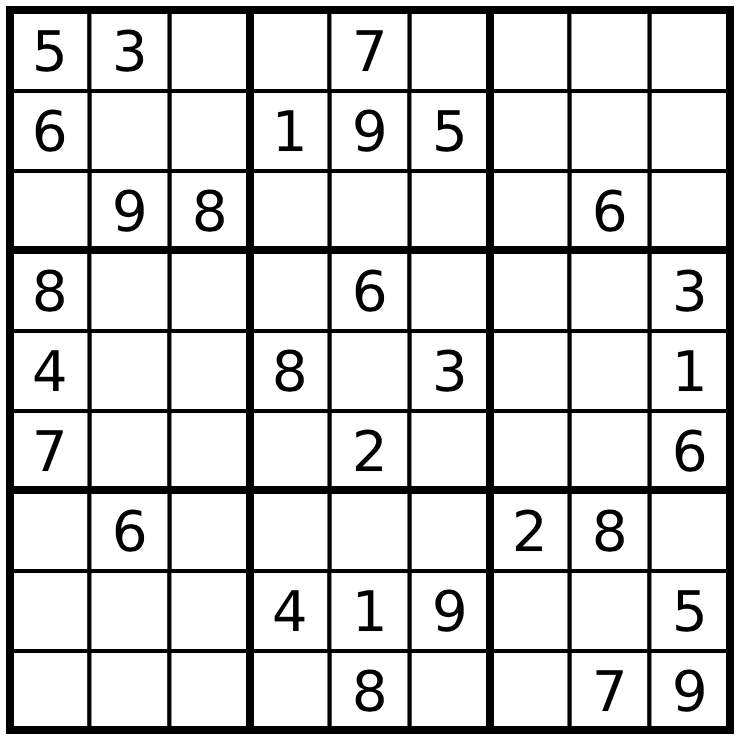
Решение судоку не является задачей оптимизации с определенной целью; на самом деле это задача допустимости: нужно найти допустимое решение, удовлетворяющее правилам. Ее можно рассматривать как задачу оптимизации с целью 0.
Формулировка частично целочисленной линейной программы
Эту задачу можно смоделировать, используя целочисленное программирование 0-1, то есть как задачу, в которой все переменные решения двоичные. Мы воспользуемся JuMP для создания модели, а затем сможем решить ее с помощью любого решателя целочисленных программ.
using JuMP
using HiGHSМы определим двоичную переменную (которая может быть равна либо 0, либо 1) для каждого возможного числа в каждой возможной ячейке. Смысл каждой переменной следующий: x[i,j,k] = 1 тогда и только тогда, когда ячейка (i,j) содержит число k, где i — строка, а j — столбец.
Создадим модель:
sudoku = Model(HiGHS.Optimizer)
set_silent(sudoku)Создадим переменные:
@variable(sudoku, x[i = 1:9, j = 1:9, k = 1:9], Bin);Теперь можно начать добавлять ограничения. Начнем мы с того, что совершенно очевидно для нас, людей, но обязательно должно соблюдаться: в каждой ячейке может быть только одна цифра.
for i in 1:9 # Для каждой строки
for j in 1:9 # и каждого столбца
# Суммируем все возможные цифры. В ячейке может быть только одна из цифр,
# поэтому сумма должна быть равна единице.
@constraint(sudoku, sum(x[i, j, k] for k in 1:9) == 1)
end
endДалее добавим ограничения для строк и столбцов. Все эти ограничения настолько похожи, что их можно добавить одновременно.
for ind in 1:9 # Каждая строка ИЛИ каждый столбец
for k in 1:9 # Каждая цифра
# Сумма по столбцам (j) — ограничение для строки
@constraint(sudoku, sum(x[ind, j, k] for j in 1:9) == 1)
# Сумма по строкам (i) — ограничение для столбца
@constraint(sudoku, sum(x[i, ind, k] for i in 1:9) == 1)
end
endНаконец, нужно наложить ограничение, согласно которому каждая цифра должна встречаться только один раз в каждом из девяти сегментов сетки размером 3x3. Наша стратегия будет заключаться в обращении по индексам к левым верхним ячейкам в каждом квадрате 3x3 с помощью циклов for и последующем суммировании значений по квадратам.
for i in 1:3:7
for j in 1:3:7
for k in 1:9
# i — это строка левого верхнего угла, j — его столбец.
# Суммируем значения от i до i+2, например i=4, r=4, 5, 6.
@constraint(
sudoku,
sum(x[r, c, k] for r in i:(i+2), c in j:(j+2)) == 1
)
end
end
endПоследнее, что нужно сделать, — добавить начальное решение в виде набора ограничений. Мы решим задачу, представленную на изображении в начале руководства. Если в ячейке нет цифры, вносится значение 0.
Имеющиеся цифры:
init_sol = [
5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9
]
for i in 1:9
for j in 1:9
# Если ячейка не пустая
if init_sol[i, j] != 0
# Соответствующая переменная для этой цифры и ячейки должна
# быть равна 1.
fix(x[i, j, init_sol[i, j]], 1; force = true)
end
end
endРешаем задачу:
optimize!(sudoku)
@assert is_solved_and_feasible(sudoku)Получаем значения x:
x_val = value.(x);Создаем матрицу для хранения решения:
sol = zeros(Int, 9, 9) # Матрица целых чисел 9x9
for i in 1:9
for j in 1:9
for k in 1:9
# Целочисленные программы решаются как ряд линейных программ, поэтому
# значения могут быть не точно равны 0 и 1. Их можно округлить до
# ближайшего целого числа, чтобы упростить задачу.
if round(Int, x_val[i, j, k]) == 1
sol[i, j] = k
end
end
end
endОтобразим решение:
sol9×9 Matrix{Int64}:
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
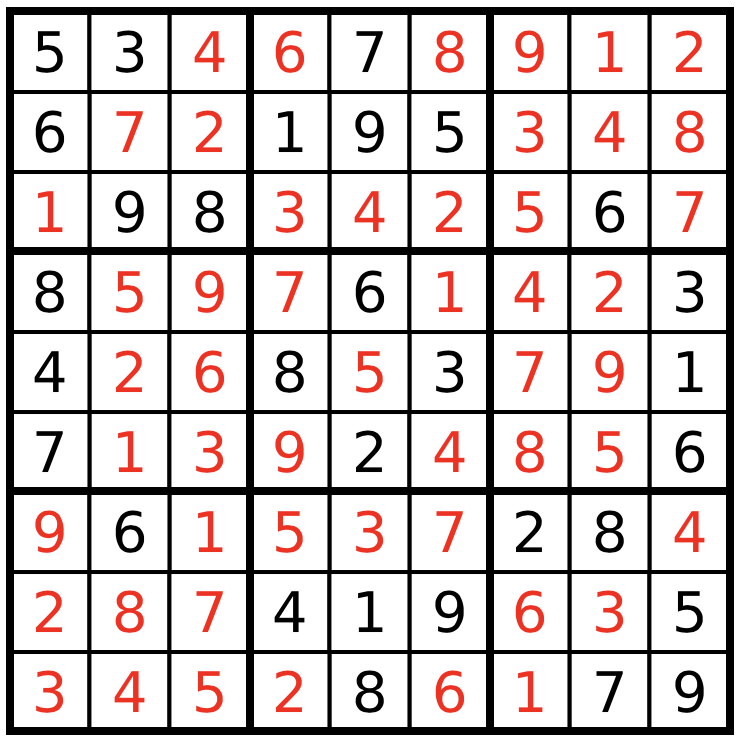
3 4 5 2 8 6 1 7 9Это правильное решение:
Формулировка программы в ограничениях
Эту задачу можно также смоделировать с помощью программирования в ограничениях и ограничения «все разные», согласно которому никакие два элемента вектора не могут иметь одинаковое значение.
Благодаря системе переформулирования в MathOptInterface эту задачу по-прежнему можно решить с помощью HiGHS.
model = Model(HiGHS.Optimizer)
set_silent(model)
# В механизме предварительного решения в версии HiGHS 1.2 есть ошибка, из-за которой эта задача классифицируется как
# недопустимая.
set_attribute(model, "presolve", "off")Вместо двоичных переменных мы напрямую определяем сетку 9x9 целочисленных значений от 1 до 9:
@variable(model, 1 <= x[1:9, 1:9] <= 9, Int);Затем мы налагаем требование, чтобы все значения в каждой из строк были разными:
@constraint(model, [i = 1:9], x[i, :] in MOI.AllDifferent(9));Все значения в каждом из столбцов также должны быть разными:
@constraint(model, [j = 1:9], x[:, j] in MOI.AllDifferent(9));И все значения в каждом квадрате 3x3 сетки также должны быть разными:
for i in (0, 3, 6), j in (0, 3, 6)
@constraint(model, vec(x[i.+(1:3), j.+(1:3)]) in MOI.AllDifferent(9))
endНаконец, как и ранее, зададим начальное решение и выполним оптимизацию:
for i in 1:9, j in 1:9
if init_sol[i, j] != 0
fix(x[i, j], init_sol[i, j]; force = true)
end
end
optimize!(model)
@assert is_solved_and_feasible(model)Отобразим решение:
csp_sol = round.(Int, value.(x))9×9 Matrix{Int64}:
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9Оно совпадает с найденным ранее:
sol == csp_soltrue