Шум Пуассона
Пуассоновский шум возникает из-за дискретного характера событий. Например, набором данных может быть микроскопическое изображение с очень ограниченной интенсивностью (например, флуоресцентный образец). В этом случае вероятность того, что будет измерено определенное количество фотонов, равна:
где — это ожидаемое значение, а — измеренное. Пуассоновский шум случайным образом выбирает значения из этого распределения.
Использование
Для массивов, изображений в оттенках серого и RGB-изображений доступен следующий метод.
poisson(X; scaling=1, clip=false)X — это массив.
Пуассоновский шум применяется к каждому элементу массива в отдельности, где определяется самим значением. Однако, например, датчики измеряют не непосредственно количество фотонов, а их интенсивность. scaling является необязательным аргументом, позволяющим связать интенсивность с рядом дискретных событий. Например, обычно можно определить, что самый высокий пиксель в измеренных данных соответствует 100 фотонам, в этом случае вы указываете scaling=100 в методе. Обычно требуется указать этот параметр. Если вы предоставляете массив, который уже содержит целые числа, соответствующие измеренным дискретным событиям, можно опустить scaling.
Примеры
Вот несколько примеров с изображениями.
using Noise, TestImages, Images
img_gray = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
# наибольшая интенсивность соответствует 10 фотонам
img_gray_noise = poisson(img_gray, 10.0)
# наибольшая интенсивность соответствует 1000 фотонам
img_gray_noise_heavy = poisson(img_gray, 1000.0)
img_color_noise = poisson(img_color, 100.0)Как видно, изображение с большим количеством измеренных фотонов меньше подвержено влиянию шума.
| Изображение с оттенками серого с 10-ю фотонами при самом ярком значении | Изображение с оттенками серого с 1000 фотонов при самом ярком значении | RGB-изображение со 100 фотонами при самом ярком значении |
|---|---|---|
|
|
|
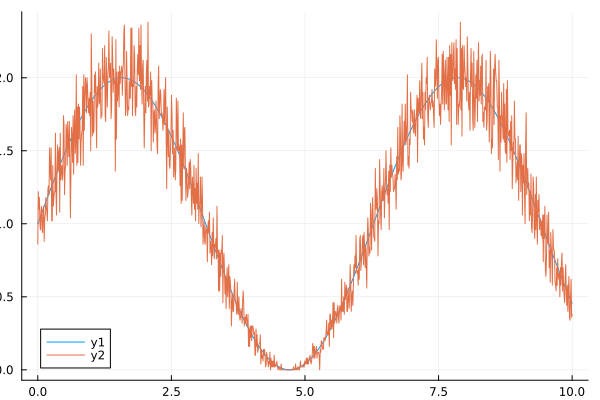
Одномерные массивы
Пуассоновский шум по своей природе не может работать с отрицательными вхождениями, поэтому одномерный массив представляет собой синусоидальную кривую, сдвинутую по оси y.
using Noise, Plots
x = LinRange(0.0, 10.0, 1000)
y = 1 .* sin.(x) .+ 1
# небольшой шум
y_noise = poisson(y, 100)
# сильный шум и сдвиг среднего
plot(x,y);
plot!(x, y_noise);qt.qpa.xcb: could not connect to display qt.qpa.plugin: Could not load the Qt platform plugin "xcb" in "" even though it was found. This application failed to start because no Qt platform plugin could be initialized. Reinstalling the application may fix this problem. Available platform plugins are: linuxfb, minimal, offscreen, vnc, xcb. Aborted connect: Connection refused GKS: can't connect to GKS socket application GKS: Open failed in routine OPEN_WS GKS: GKS not in proper state. GKS must be either in the state WSOP or WSAC in routine ACTIVATE_WS
Мы видим, что количество шума, в отличие от аддитивного шума, выше для более высоких значений интенсивности. Однако соотношение сигнал/шум лучше при более высоких значениях интенсивности. Это было видно на изображении Фабио.