Реализация AbstractMCMC в Turing
Введение
Рассмотрим блок кода Turing:
@model function gdemo(x, y)
s² ~ InverseGamma(2, 3)
m ~ Normal(0, sqrt(s²))
x ~ Normal(m, sqrt(s²))
y ~ Normal(m, sqrt(s²))
end
mod = gdemo(1.5, 2)
alg = IS()
n_samples = 1000
chn = sample(mod, alg, n_samples)Функция sample является частью интерфейса AbstractMCMC. Как объясняется в руководстве по интерфейсу, создание метода выборки, который может быть использован sample, заключается в перегрузке структур и функций в AbstractMCMC. В руководстве по интерфейсу также приведен отдельный пример реализации [AdvancedMH.jl].
Методы выборки Turing (большинство из которых приведены здесь) также реализуют AbstractMCMC. Turing определяет особую архитектуру для реализаций AbstractMCMC, которая позволяет работать с моделями, определенными макросом @model, и использует DynamicPPL в качестве бэкенда. Цель этой статьи — описать эту архитектуру и рассказать о том, как реализовать собственный метод выборки в Turing, используя выборку по значимости в качестве примера. Мы не будем вдаваться во все детали: например, здесь не рассматриваются селекторы или параллелизм.
Сначала мы узнаем, как работает выборка по значимости в абстрактном виде. Рассмотрим модель, определенную в первом блоке кода. Математически это можно записать так.
Латентные переменные — это и , наблюдаемые переменные — это и . Модель совместного распределения разлагается на априорное распределение и правдоподобие . Поскольку и наблюдаются, цель состоит в том, чтобы вывести апостериорное распределение .
Выборка по значимости выполняет независимые выборки из априорного распределения. Она также выводит ненормализованные веса,
так что эмпирическое распределение
является хорошей аппроксимацией для апостериорного.
1. Определение сэмплера (Sampler)
Вспомните последнюю строку приведенного выше блока кода:
chn = sample(mod, alg, n_samples)Здесь sample принимает в качестве аргументов модель mod, алгоритм alg и количество выборок n_samples и возвращает экземпляр chn Chains, который может быть проанализирован с помощью функций в MCMCChains.
Модели
Чтобы определить модель, следует объявить совместное распределение по переменным в макросе @model и указать, какие переменные являются наблюдаемыми, а какие должны быть выведены, а также значения наблюдаемых переменных. Таким образом, при реализации выборки по значимости
mod = gdemo(1.5, 2)создает экземпляр mod структуры Model, который соответствует наблюдениям значения 1.5 для x и значения 2 для y.
Алгоритмы
Алгоритм — это просто метод выборки: в Turing он является подтипом абстрактного типа InferenceAlgorithm. Для определения алгоритма может потребоваться указать несколько параметров высокого уровня. Например, «гамильтониан Монте-Карло» может быть слишком расплывчатым, но «гамильтониан Монте-Карло с 10 шагами с перешагиванием для каждого предложения и размером шага 0,01» — это алгоритм. «Метрополис-Гастингс» может быть слишком расплывчатым, но «Метрополис-Гастингс с распределением предложений p» — это алгоритм. Таким образом
stepsize = 0.01
L = 10
alg = HMC(stepsize, L)определяет алгоритм гамильтониана Монте-Карло, экземпляр HMC, который является подтипом InferenceAlgorithm.
В случае выборки по значимости нет необходимости указывать дополнительные параметры:
alg = IS()определяет алгоритм выборки по значимости, экземпляр IS, который является подтипом InferenceAlgorithm.
При создании собственного метода выборки Turing вы должны построить подтип InferenceAlgorithm, соответствующий вашему методу.
Сэмплеры
Сэмплеры — это не то же самое, что и алгоритмы. Алгоритм — это универсальный метод выборки, а сэмплер представляет собой объект, хранящий информацию о том, как алгоритм и модель взаимодействуют во время выборки, и изменяемый по мере выполнения выборки. Структура Sampler определяется в DynamicPPL.
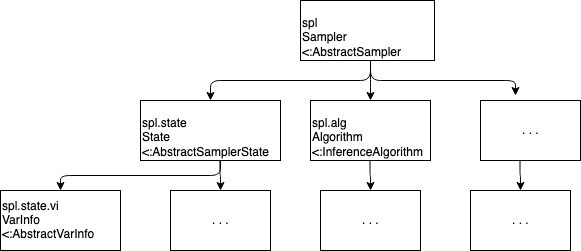
Turing реализует AbstractSampler из AbstractMCMC с помощью структуры Sampler, определенной в DynamicPPL. Наиболее важными атрибутами экземпляра spl сэмплера (Sampler) являются следующие.
-
spl.alg: используемый метод выборки, экземпляр подтипаInferenceAlgorithm; -
spl.state: информация о процессе выборки (см. ниже).
Когда вы вызываете sample(mod, alg, n_samples), Turing сначала использует model и alg для создания экземпляра spl сэмплера (Sampler), а затем вызывает собственную функцию AbstractMCMC sample(mod, spl, n_samples).
При определении собственного метода выборки Turing вы должны построить следующие компоненты:
-
конструктор сэмплера, который использует модель, и алгоритм для инициализации экземпляра
Sampler. Для выборки по значимости:
function Sampler(alg::IS, model::Model, s::Selector)
info = Dict{Symbol, Any}()
state = ISState(model)
return Sampler(alg, info, s, state)
end-
структура состояния, реализующая
AbstractSamplerState, соответствующее вашему методу (см. следующий абзац).
Состояния
Поле vi содержит всю важную информацию о выборке: прежде всего, значения всех образцов, а также распределения, из которых они выбраны, имена параметров модели и другие метаданные. Как мы увидим ниже, многие важные шаги во время выборки соответствуют запросам или обновлениям spl.state.vi.
По умолчанию вы можете использовать SamplerState, конкретный тип, определенный в inference/Inference.jl, который расширяет AbstractSamplerState и не имеет полей, кроме vi:
mutable struct SamplerState{VIType<:VarInfo} <: AbstractSamplerState
vi :: VIType
endПри выполнении выборки по значимости важны не только значения образцов, но и их веса. Ниже мы увидим, что вес каждого образца также прибавляется к spl.state.vi. Более того, среднее значение
весов образцов является особенно важной величиной:
-
она используется для нормализации эмпирической аппроксимации апостериорного распределения
-
ее логарифм — это оценка выборки по значимости доказательства логарифма .
Чтобы избежать необходимости повторных вычислений, is.jlопределяет специфичный для выборки по значимости конкретный тип ISState для состояний сэмплера с дополнительным полем final_logevidence, содержащим
mutable struct ISState{V<:VarInfo, F<:AbstractFloat} <: AbstractSamplerState
vi :: V
final_logevidence :: F
end
# дополнительный конструктор
ISState(model::Model) = ISState(VarInfo(model), 0.0)На следующей схеме приводится обобщенный вид представленной выше иерархии.
2. Перегрузка функций, используемых внутри mcmcsample
Многое здесь зависит от метода. Однако в Turing также есть функции, которые облегчают реализацию этих функций.
Переходы
AbstractMCMC хранит информацию, соответствующую каждому отдельному образцу, в объектах, называемых переходами (transition), но не указывает, какой может быть структура этих объектов. Вы можете принять решение о реализации типа MyTransition для переходов, соответствующий специфике ваших методов. Однако существует множество ситуаций, в которых единственная информация, необходимая для каждого образца, — это:
-
его значение:
-
логарифм совместной вероятности наблюдаемых данных и данной выборки:
lp
Inference.jl определяет структуру Transition, которая соответствует этой ситуации по умолчанию.
struct Transition{T, F<:AbstractFloat}
θ :: T
lp :: F
endПринцип работы sample
Примерная схема, в которой не учитываются такие вещи, как параллелизм, выглядит следующим образом:
sample вызывает функцию mcmcsample, которая вызывает
-
sample_init!для настройки всего необходимого -
step!многократно, чтобы создать несколько новых переходов -
sample_end!для выполнения операций после получения всех образцов -
bundle_samplesдля преобразования вектора переходов в более подходящий тип, напримерChain.
Конечно, вы можете реализовать все эти функции, но AbstractMCMC и Turing также предоставляют реализации по умолчанию для простых случаев. Например, выборка по значимости использует стандартные реализации sample_init! и bundle_samples, поэтому вы не увидите код для них внутри is.jl.
3. Перегрузка assume и observe
Упомянутые выше функции, такие как sample_init!, step! и т. д., конечно же, должны использовать информацию о модели для создания образцов. В частности, этим функциям могут понадобиться образцы из распределений, определенных в модели, или оценка плотности этих распределений при некоторых значениях соответствующих параметров или наблюдений.
В качестве примера первого варианта рассмотрим выборку по значимости, как это определено в is.jl. Эта реализация выборки по значимости использует априорное распределение модели в качестве распределения предложения, и поэтому для нее требуются образцы из априорного распределения модели. Другой пример — приближенное байесовское вычисление, для которого требуется несколько образцов из априорного распределения и распределения вероятности модели, чтобы сгенерировать один образец.
Примером последнего является алгоритм Метрополиса-Гастингса. На каждом шаге выборки из целевого апостериорного распределения
для вычисления коэффициента принятия необходимо оценить совместную плотность модели
с помощью образца из предложения и наблюдаемых данных .
В связи с этим возникает вопрос: как эти функции могут получить доступ к информации о модели во время выборки? Напомним, что модель хранится как экземпляр m модели (Model). Одним из атрибутов m является функция оценки модели m.f, которая строится путем компиляции макроса @model. При выполнении f по порядку запускаются операторы тильды модели, и на каждом шаге информация о модели добавляется в сэмплер (экземпляр Sampler, хранящий информацию о текущем процессе выборки) (дополнительные сведения о компиляции макроса @model см. здесь). Функции DynamicPPL assume и observe определяют, какую информацию добавлять в сэмплер для каждого оператора тильды.
Рассмотрим экземпляр m модели (Model) и сэмплер spl со связанными VarInfo vi = spl.state.vi. В какой-то момент в процессе выборки функция AbstractMCMC, например step!, вызывает функцию m(vi, ...), которая вызывает функцию оценки модели m.f(vi, ...).
-
Для каждого оператора тильды в макросе
@modelфункцияm.f(vi, ...)возвращает информацию, связанную с моделью (образцы, значение плотности модели и т. д.), и добавляет ее вvi. Как это происходит?-
Вспомним, что код для
m.f(vi, ...)автоматически генерируется при компиляции макроса@model. -
Для каждого оператора тильды в объявлении
@modelэтот код содержит вызовassume(vi, ...), если переменная в LHS тильды является выводимым параметром модели, иobserve(vi, ...), если переменная в LHS тильды является наблюдением. -
В файле, соответствующем вашему методу выборки (т. е. в
Turing.jl/src/inference/<your_method>.jl), вы перегрузилиassumeиobserve, чтобы они могли изменитьviдля включения необходимых информации и образцов. -
Как минимум,
assumeиobserveвозвращают логарифмическую плотностьlpобразца или наблюдения. Затем функция оценки модели немедленно вызывает функциюacclogp!!(vi, lp), которая добавляетlpк значению логарифмической совместной плотности, хранящемуся вvi.
-
Вот как выглядит assume для выборки по значимости:
function DynamicPPL.assume(rng, spl::Sampler{<:IS}, dist::Distribution, vn::VarName, vi)
r = rand(rng, dist)
push!(vi, vn, r, dist, spl)
return r, 0
endСначала функция генерирует образец r из распределения dist (правая часть оператора тильды). Затем она добавляет r в vi и возвращает r и 0.
Функция observe еще проще:
function DynamicPPL.observe(spl::Sampler{<:IS}, dist::Distribution, value, vi)
return logpdf(dist, value)
endОна просто возвращает плотность (в дискретном случае — вероятность) наблюдаемого значения при распределении dist.
4. Сводка: пошаговое выполнение алгоритма выборки по значимости
Мы сосредоточимся на функциях AbstractMCMC, которые переопределяются в is.jl и выполняются внутри mcmcsample: step!, которая вызывается n_samples раз, и sample_end!, которая выполняется один раз после этих n_samples итераций.
-
Во время -й итерации
step!выполняет три операции:-
empty!!(spl.state.vi): удаляет информацию о предыдущем образце изVarInfoсэмплера -
model(rng, spl.state.vi, spl): вызывает функцию оценки модели-
вызовы
assumeдобавляют образцы из априорных распределений и вspl.state.vi -
после вызовов
assumeилиobserveследует строкаacclogp!!(vi, lp), гдеlp— это выводassumeиobserve -
для
lpзадается 0 послеassume, а также значение плотности в наблюдении послеobserve -
когда все операторы тильды выполнены,
spl.state.vi.logp[]— это суммаlp, т. е правдоподобие наблюдений с учетом образцов латентных переменных и .
-
-
return Transition(spl): строит переход из сэмплера и возвращает этот переход-
поле
viперехода — это простоspl.state.vi -
поле
lpсодержит правдоподобиеspl.state.vi.logp[].
-
-
-
Когда итерации
n_samplesзавершены,sample_end!заполняет полеfinal_logevidenceвspl.state-
функция просто берет логарифм среднего значения весов образцов, используя логарифмические веса для численной устойчивости.
-