Аппроксимация данных
Аппроксимация данных — приложение Engee для подбора аналитической зависимости между двумя наборами точек (например, Вектор X и Вектор Y). Приложение автоматически находит параметры выбранной модели, строит кривую поверх исходных данных и рассчитывает метрики качества. Это эффективно для экономии времени: без программирования вы можете получить наглядные графики и готовое выражение функции.
Чтобы открыть приложение, перейдите на страницу с примером и поочередно нажмите Открыть пример в Engee → Старт Engee → Сохранить и открыть. Это откроет файл engee_curve_fitting_app.ngscript в редакторе скриптов ![]() в рабочем пространстве Engee.
в рабочем пространстве Engee.
Для запуска приложения следуйте инструкциям, указанным в файле engee_curve_fitting_app.ngscript. После запуска приложение для аппроксимации данных откроется в отдельной вкладке браузера:
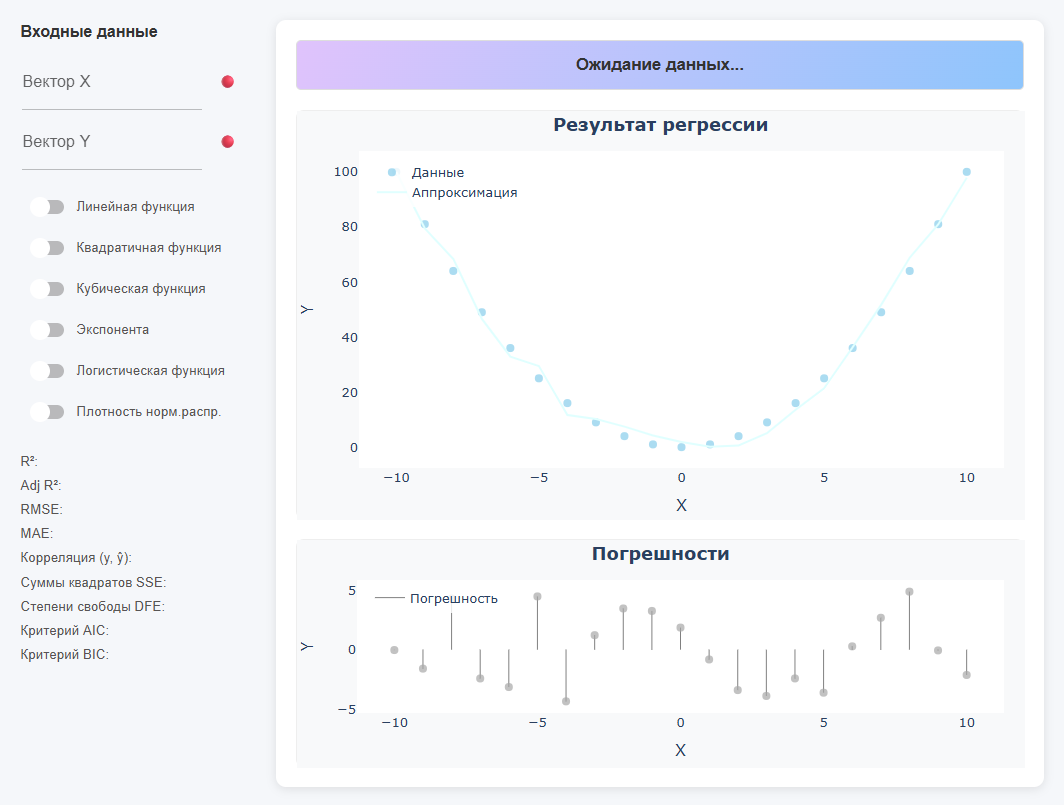
Верхняя цветная строка показывает уравнение найденной функции (если данных нет, то пишет «Ожидание данных…»). Слева расположена панель для ввода входных данных и для выбора типа функции, а также вывод метрик. В центре — два графика: Результат регрессии (точки + кривая) и Погрешности (остатки).
Ввод данных
Приложение читает данные из рабочего пространства Engee (значения должны появиться в окне переменных  ). В полях Вектор X и Вектор Y укажите имена доступных переменных. Рядом с полями отображаются индикаторы состояния:
). В полях Вектор X и Вектор Y укажите имена доступных переменных. Рядом с полями отображаются индикаторы состояния:
-
🔴 — вектор не найден;
-
🟡 — задан только один вектор, либо векторы не совпадают по длине, расчет модели не запущен;
-
🟢 — векторы заданы, модель построена.
|
Требования к данным:
|
Это основной способ работы с входными данными, однако приложение поддерживает и другие варианты ввода данных:
-
Прямое задание массивов
X = [1, 2, 3, 4, 5] Y = [2.1, 4.0, 5.9, 8.3, 10.2]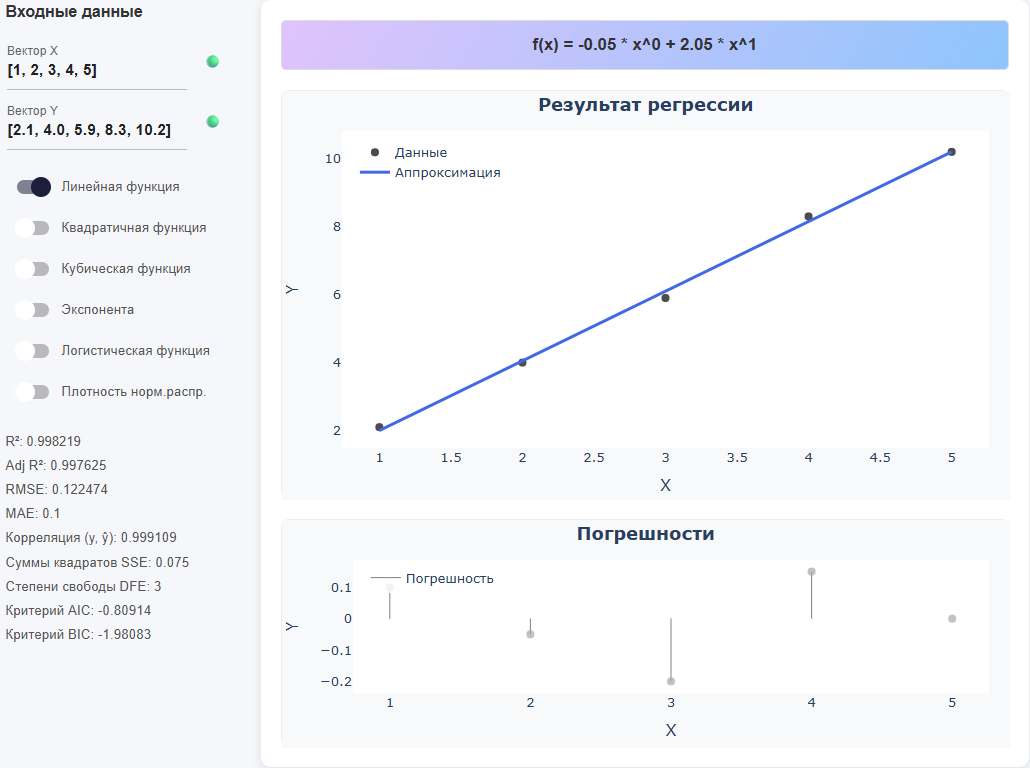
-
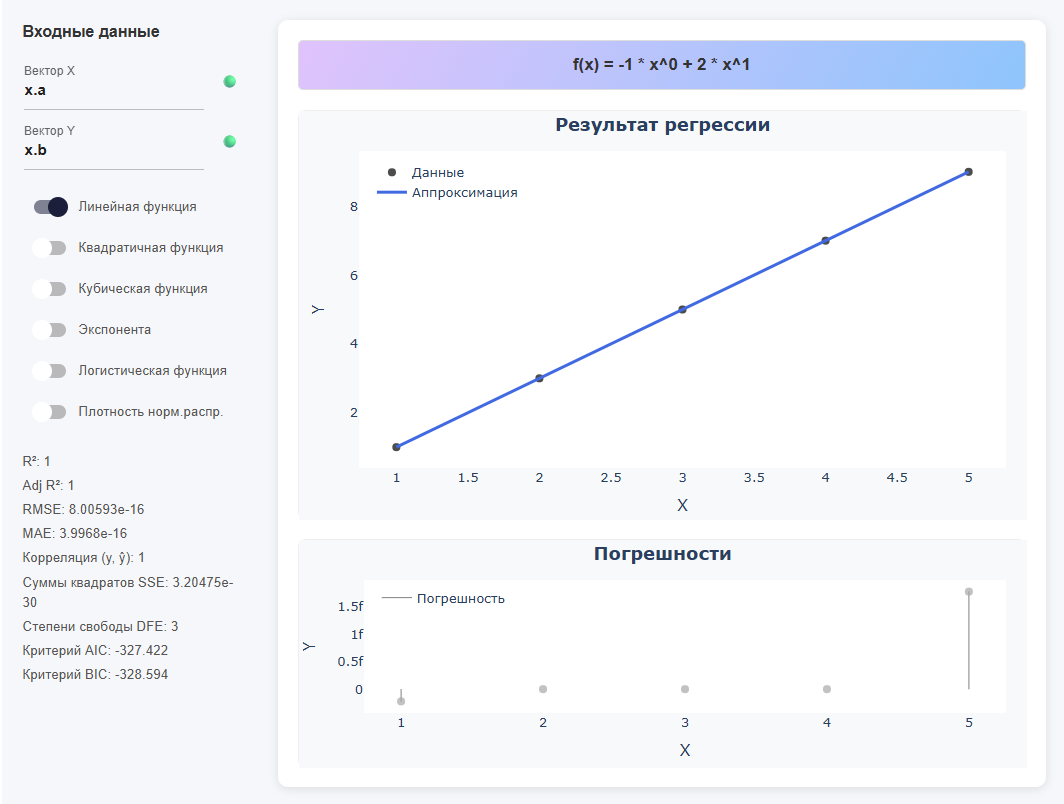
Из DataFrame по столбцам
using DataFrames x = DataFrame(a = [1,2,3,4,5], b = [1,3,5,7,9])Вывод:
5×2 DataFrame Row │ a b │ Int64 Int64 ─────┼────────────── 1 │ 1 1 2 │ 2 3 3 │ 3 5 4 │ 4 7 5 │ 5 9Тогда в приложении:
-
Как выражения (операции над массивами)
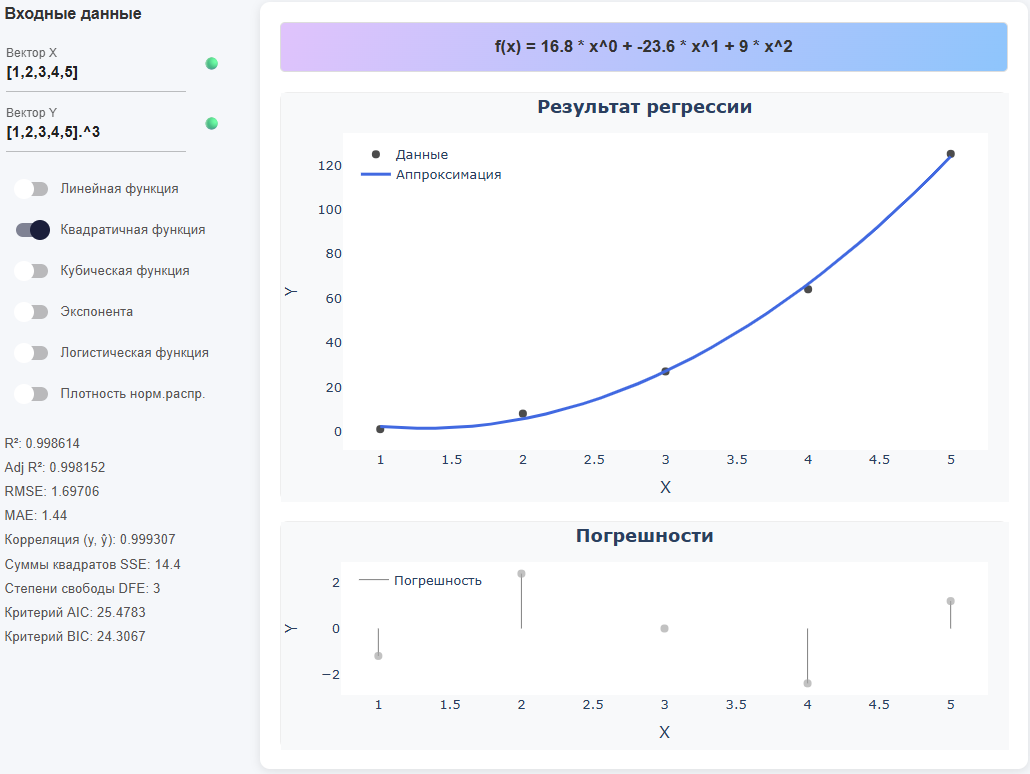
-
Гибрид переменной и выражения
X = [1,2,3,4,5] Y = X .^ 3 # Поэлементное возведение в степень (точка перед ^ обязательна)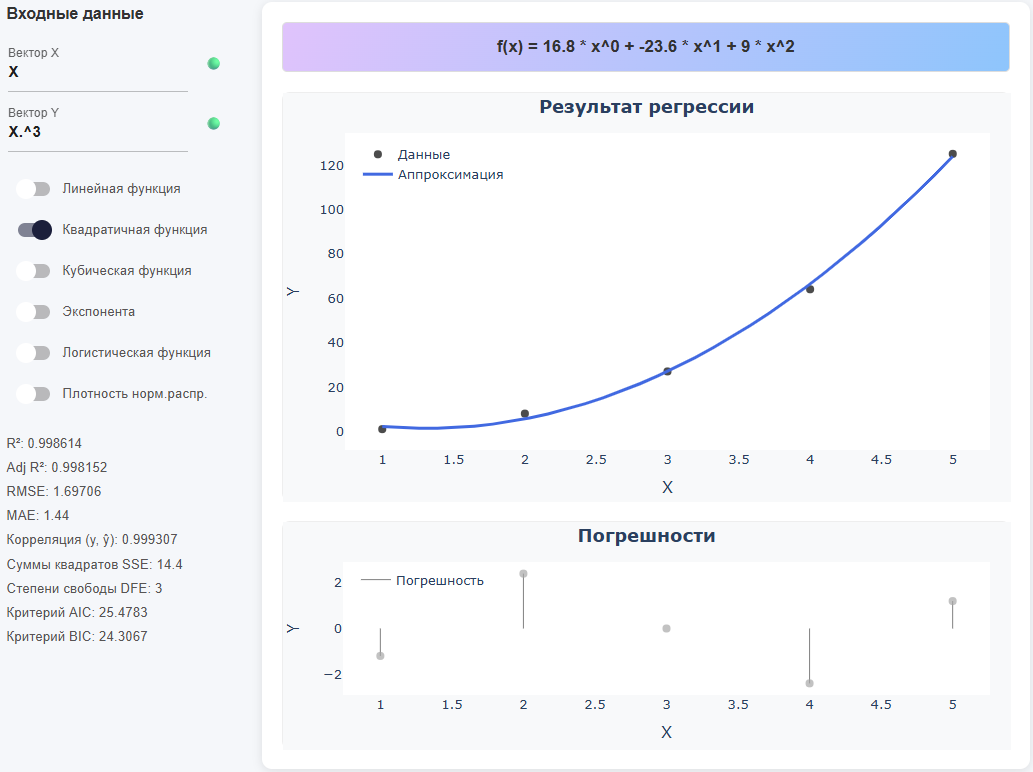
Выбор функции аппроксимации
В левой панели включите один из переключателей:
-
Линейная функция — описывает постоянную скорость изменения величины без кривизны; подходит для приблизительно прямолинейных трендов и быстрого «первого приближения». Уравнение: .
-
Квадратичная функция — захватывает одну «дугу» (параболическую кривизну) и позволяет моделировать наличие единственного экстремума (минимума/максимума). Уравнение: .
-
Кубическая функция — дает возможность моделировать перегиб (смену кривизны) и асимметричные профили; полезна при S-образных тенденциях без насыщения. Уравнение: .
-
Экспонента — описывает пропорциональный рост/спад, когда относительное изменение примерно постоянно; требует положительных значений
Y, параметры подбираются через линеаризациюln(y). Уравнение: . -
Логистическая функция — модель ограниченного роста с насыщением (S-образная кривая); подходит для долей/вероятностей и величин с естественными пределами (нижним и верхним). Уравнение: .
-
Плотность норм. распр. — подгоняет «колокол» Гаусса к симметричным пиковым данным; уместна, когда
Yотражает плотность/частоты вокруг среднего со спадом к краям. Уравнение: .
| Для полиномов выбирайте порядок, который оправдан данными. Избыточная сложность может ухудшить обобщающую способность. Сравнивайте модели по Adj R2, AIC и BIC. |
Метрики качества
После каждой аппроксимации рассчитываются метрики (выводятся под списком функций):

-
R2 (коэффициент детерминации) — показывает долю вариации
Y, объясненную моделью; лежит в диапазоне 0..1 (ближе к 1 — лучше). Важно: высокий R2 не гарантирует отсутствие смещения и «хорошие» остатки. -
Adj R2 (скорректированный R2) — версия R2 с учетом числа параметров модели; штрафует избыточную сложность и потому честнее при сравнении разных моделей. Формула:
гдеn— число точек,p— число признаков (без константы). -
RMSE — корень из среднеквадратичной ошибки (единицы совпадают с
Y); удобно как «типичный масштаб» ошибки. Формулы: , . -
MAE — средняя абсолютная ошибка; интерпретируется «в тех же единицах», менее чувствительна к выбросам, чем RMSE. Полезна, когда важна «средняя по модулю» погрешность.
-
Корреляция (y, ŷ) — линейная связь между фактическими
yи предсказаниямиŷ(от −1 до 1). Высокая корреляция означает согласованность направления, но не гарантирует малые ошибки или корректную форму модели. -
Сумма квадратов ошибок (SSE) — ; базовая «стоимость» для многих методов. Зависит от масштаба данных, поэтому сама по себе хуже подходит для сравнения разных наборов.
-
Степени свободы (DFE) — обычно (точек минус параметры и константа); используется при расчете дисперсий, доверительных оценок и Adj R2.
-
Критерий AIC — информационный критерий: баланс качества подгонки и числа параметров; сравнивают только модели на одном и том же наборе данных. Меньше — лучше; абсолютное значение не интерпретируют.
-
Критерий BIC — как AIC, но с более жестким штрафом за сложность (сильнее предпочитает простые модели). Меньше — лучше.
| При выборе модели ориентируйтесь на Adj R2/AIC/BIC в совокупности с анализом графика остатков: случайные, «бесструктурные» остатки — признак адекватной модели; систематический рисунок — повод выбрать другой вид функции. |
Работа с графиками
-
Результат регрессии — черные точки (исходные данные) и синяя линия (модель):
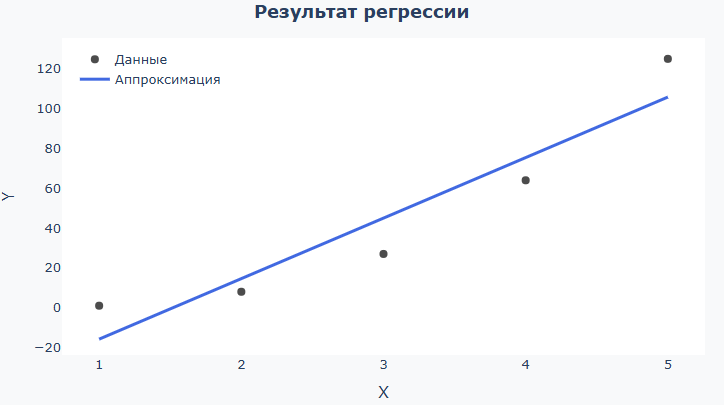
Смотрите, насколько линия совпадает с вашими ожиданиями, прилегает «по облаку» точек по всему диапазону. Если данные простые, а линия слишком извивается — модель, скорее всего, слишком сложная. Если линия почти прямая, а многие точки расположены слишком далеко от нее — модель слишком простая. Для логистической функции проверьте, что линия плавно «насыщается» к границам. Для нормальной плотности — проверьте, что «колокол» по форме и ширине похож на данные. Если вы хотите убрать из рассмотрения какой-то диапазон данных (например, точки по краям вектора), в поле ввода вместо
x_dataиy_dataможно вписатьx_data[10:end-10]иy_data[10:end-10]. Таким образом вы построите модель для всех точек, кроме 10 крайних (с обеих сторон). -
Погрешности — столбики разностей
y − ŷс линией нуля:
Хороший признак — столбики остатков располагаются вокруг линии 0 в случайных направлениях, с примерно одинаковой амплитудой отклонений без явного рисунка. Если просматривается «узор» (дуга, волна) или столбики имеют смещение — скорее всего выбрана неправильная по форме модель. Если к краям столбики становятся заметно выше — ошибки растут на границах (возможно, не хватает данных или выбран не тот тип функции). Отдельные очень высокие столбики — это выбросы; их стоит проверить отдельно или исключить из вектора, чтобы получить более чистые метрики.
Для удобной работы с графиками доступен функционал библиотеки Plotly:

-
 — скачать график как PNG;
— скачать график как PNG; -
 — возможность выделить область и увеличить ее содержимое;
— возможность выделить область и увеличить ее содержимое; -
 — инструмент перемещения графика на координатной плоскости;
— инструмент перемещения графика на координатной плоскости; -
 — увеличивает масштаб координатной плоскости;
— увеличивает масштаб координатной плоскости; -
 — уменьшает масштаб координатной плоскости;
— уменьшает масштаб координатной плоскости; -
 — возвращает масштаб координатной плоскости по умолчанию;
— возвращает масштаб координатной плоскости по умолчанию; -
 — сброс координатных осей.
— сброс координатных осей.
Проверка результата в командной строке Engee
-
Скопируйте уравнение модели из верхней строки приложения. Например:
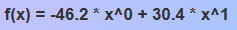
-
Вставьте выражение в командную строку
 и постройте график:
и постройте график:# Пример: вставьте выражение из приложения f(x) = -46.2 * x^0 + 30.4 * x^1 # Постройте значения f на отрезке 1..10 plot(1:10, f) -
График будет построен в окне графиков Engee:
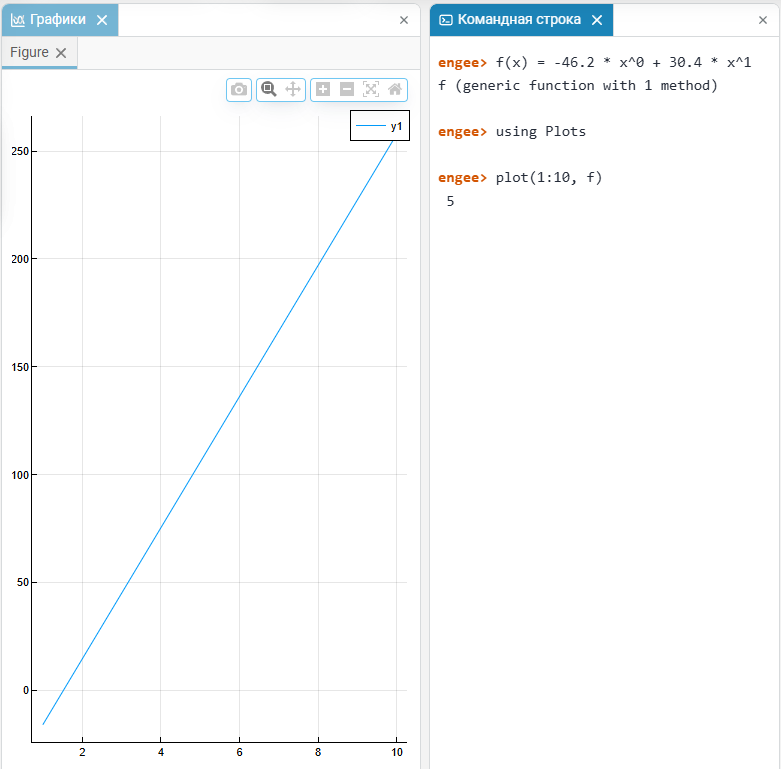
Если уравнение предполагает поэлементные операции над вектором, то используйте синтаксис с точками: .^, .*, ./.
|
Короткий сценарий работы
-
Загрузите входные данные в Engee. Например, объявите
XиY(переменные, массивы, DataFrame или выражение). -
Укажите векторы
XиYкак входные данные в приложении и выберите нужный тип функции. -
Сравните метрики (Adj R2, AIC, BIC) для разных функций и визуально оцените график остатков.
-
Скопируйте полученное уравнение и используйте его в дальнейших расчетах в Engee.