Engee 文档

过滤器

一维数字滤波器。

库::`工程师`

语法

函数调用

  • [参数:y]=过滤器(<参数:b>>,<参数:a>>,<参数:x>>) -过滤输入数据 [参数:x] 使用由分子和分母的系数确定的有理传递函数 [参数:b] 和 [参数:a].

    有关理性传递函数的更多信息，请参阅理性传递函数。

    如果 a(1) 不等于 1，则函数 *过滤器*通过归一化滤波器系数 a(1). 因此, a(1) 必须是非零。

    • 如果 [参数:x] -矢量，然后 *过滤器*将过滤后的数据返回为与 [参数:x].

    • 如果 [参数:x] -矩阵，然后 *过滤器*对第一个维度进行操作，并返回每列的筛选数据。

    • 如果 [参数:x] -一个多维数组，然后 *过滤器*作用于数组的第一维，其大小不等于 1.

  • [参数:y]=过滤器(<参数:b>>,<参数:a>>,<参数:x>>,<参数:zi>>) -使用初始条件 [参数:zi] 于滤波器延迟。 长度 [参数:zi] 必须等于 max(length(a),length(b))-1.

  • [参数:y],[参数:zf]=过滤器(_;out=2) -也返回结束条件 [参数：zf] 对于滤波器延迟，使用前面的任何语法。 如果指定 出=1 然后 *过滤器*返回一个输出参数。

争论

输入参数

# b — 传递函数分子的系数

+ 标量,标量| 向量资料 |通过：[矩阵]

Details

传递函数分子的系数，指定为标量、矢量或矩阵。

有关理性传递函数的详细信息，请参阅理性传递函数。

数据类型

漂浮64, 漂浮物32, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64</无翻译> 支持复数::是

# 一个 — 传递函数分母的系数

+ 标量,标量| 向量资料 |通过：[矩阵]

Details

传递函数分母的系数，指定为标量、矢量或矩阵。

有关理性传递函数的详细信息，请参阅理性传递函数。

数据类型

漂浮64, 漂浮物32, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64</无翻译> 支持复数::是

# x — 输入数据

+ 传递：[向量] | 通过：[矩阵] | 传：[N维数组]

Details

输入指定为向量、矩阵或N维数组的数据。

数据类型

漂浮64, 漂浮物32, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64</无翻译> 支持复数::是

# 子 — 滤波器延迟的初始条件

+ 通行证：[[]] （默认情况下）| 传递：[向量] | 通过：[矩阵] | 传：[N维数组]

Details

滤波器延迟的初始条件，指定为矢量、矩阵或N维数组:

  • 如果 子 -矢量，那么它的长度应该等于 max(length(a),length(b))-1.

  • 如果 子 是矩阵还是N维数组，那么初始维度的大小应该是 max(length(a),length(b))-1. 每个剩余维度的大小必须与相应维度的大小相匹配 [参数:x]. 例如，考虑使用的可能性 *过滤器*在第二维度（<参数：暗淡>=2)阵列 [参数:x] 尺寸为3乘4乘5。 阵列 子 必须有一个大小 [最大(长度(<参数:A>>),长度(<参数:b>>))-1] 3乘5。

指定为的默认值 [] 将所有滤波器延迟初始化为零。

数据类型

漂浮64, 漂浮物32, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64</无翻译> 支持复数::是

# 昏暗 — 用于执行滤波的测量

+ 通行证：[标量]

Details

用于执行滤波的测量，指定为正整数标量。 如果未指定维度，则默认情况下将使用大小不相等的数组的第一个维度。 1.

考虑二维输入数组 [参数:x].

如果 昏暗 超过 ndims(x)，则 *过滤器*认为[参数:x]就好像它有额外的维度到 昏暗 与尺寸 1. 例如，如果 [参数:x] -一个2乘3矩阵，一个 暗淡=3 然后 *过滤器*在第三维度工作 [参数:x] 好像它的大小是2乘3乘1。

数据类型

漂浮64, 漂浮物32, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64</无翻译>

输出参数

# y — 过滤后的数据

+ 传递：[向量] | 通过：[矩阵] | 传：[N维数组]

Details

作为与输入数据大小相同的向量、矩阵或N维数组返回的筛选数据 [参数:x].

如果 [参数:x] 有一个类型 漂浮物32 然后 *过滤器*最初以单精度执行计算，以及 y 它也有一个类型 漂浮物32. 否则的话, y 作为类型返回 漂浮64.

数据类型

漂浮64, 漂浮物32</无翻译>

# 采埃孚 — 滤波器延迟的结束条件

+ 传递：[向量] | 通过：[矩阵] | 传：[N维数组]

Details

滤波器延迟的最终条件，作为向量、矩阵或N维数组返回。

  • 如果 [参数:x] -矢量，然后 采埃孚 -长度列向量 max(length(a),length(b))-1.

  • 如果 [参数:x] 是矩阵还是N维数组，则 采埃孚 -此长度的列向量数组 max(length(a),length(b))-1 什么是列的数量 采埃孚 相当于 [参数:x]. 例如，考虑使用的可能性 *过滤器*在第二维度（<参数：暗淡>=2)阵列 [参数:x] 尺寸为3乘4乘5。 阵列 采埃孚 将有一个大小 [最大(长度(<参数:A>>),长度(<参数:b>>))-1] 3乘5。

数据类型

漂浮64, 漂浮物32</无翻译>

例子：

移动平均滤波器

Details

移动平均滤波器是平滑噪声数据的常用方法。 在本例中，滤波器函数用于计算数据向量的平均值。

创建大小的向量字符串 1 上 100 随机噪声失真的正弦数据。

import EngeeDSP.Functions: filter
using Random
Random.seed!(0)
t = range(-pi, pi, length=100)
x = sin.(t) + 0.25 * randn(length(t))

移动平均滤波器移动窗口长度 窗口大小 沿着数据，计算包含在每个窗口中的数据的平均值。 下面的差分方程定义了矢量的移动平均滤波器 :

对于大小为 5 让我们计算有理传递函数的分子和分母的系数。

windowSize = 5
b = (1/windowSize) * ones(windowSize)
a = [1.0]

让我们找到数据的移动平均值并将其与原始数据进行比较。

y = filter(b, a, x)

plot(t, x,
     label="Input Data",
     linewidth=1.5,
     grid=true)

plot!(t, y,
      label="Filtered Data",
      linewidth=2,
      color=:red)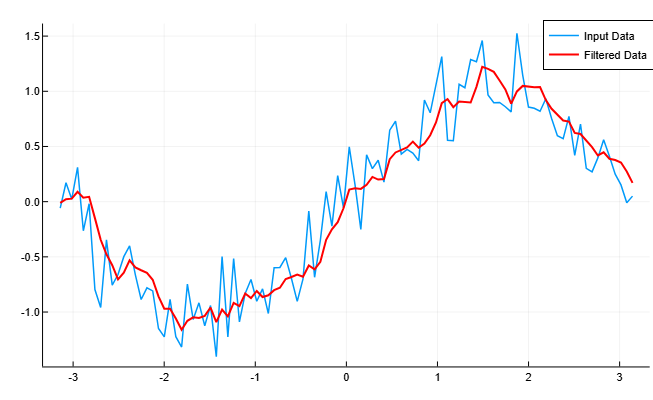

filter 4

此外

理性传递函数

Details

函数的输入和输出的描述 *过滤器*对于域中的向量，Z变换是有理传递函数。 有理传递函数具有形式:

有理传递函数适用于具有有限脉冲响应(fir)的滤波器和具有无限脉冲响应(BIH)的滤波器[1]。 这里 -Z-输入信号x的转换, -Z-输出信号的转换 , -反馈滤波器的阶数，以及 -前馈滤波器的顺序。 关于规范化，让我们假设 .

对于离散信号与 这些元素可以用差分方程的形式表达有理传递函数:

此外，可以使用其直接形式II的转置实现来表示有理传递函数，如数字IIR滤波器的图所示。 在图上 . 如果反馈和前向滤波器的阶数不相等 ，那么高阶项可以认为相等 0. 例如，对于具有 a=[1,2] 和 乙= [2, 3, 2, 4] 我可以接受吗 一个= [1, 2, 0, 0].

filter 3

过滤器执行 *过滤器*在参考点 它由时域的差分方程确定:

默认函数是 *过滤器*将滤波器延迟初始化为零, . 通过该初始化，假定过去的输入数据和输出数据都为零。 要在当前数据中包含非零过去输入，请将当前数据的初始条件指定为滤波器延迟。 滤波器延迟可以被视为对前一个输入（和前一个输出）应用相同的传递函数所产生的结束条件。 您可以指定第四个输入参数。 [参数:zi] 使用时 *过滤器*设置滤波器延迟, 子(k). 您还可以指定第二个输出参数。 [参数：zf] 使用时 *过滤器*访问最终条件, 采埃孚(k).

文学作品

  1. Oppenheim，Alan V.，Ronald W.Schafer和John R.Buck。 实时信号处理。 Upper Saddle River，NJ：Prentice-Hall，1999。