dpss
离散的细长球状序列(Slepyan sequences)。
库::`工程师`
语法
函数调用
-
[参数:dpseq],[参数:lambda]=dpss(<参数:seqLength>>,[参数:timeHalfBW])-返回第一个round(2*timeHalfBW)长度的离散细长球状序列(DPSS)[参数:seqLength]和能量集中比[参数:lambda]列向量的频域中[参数:dpsSeq]. 这些比率表示带宽中的能量量的比率。 到范围内的总能量 ,在哪里 -采样率。
-
[参数:dpseq],[参数:lambda]=dpss(<参数:seqLength>>,[参数:timeHalfBW],[参数:numSeq])-返回第一个[参数:numSeq]时间和带宽一半乘积的DPSS序列[参数:timeHalfBW]. 该函数按其能量集中比的顺序返回序列。
-
[参数:dpsSeq],[参数:lambda]=dpss(_,[参数:dpssLength])-插值长度的DPSS序列[参数:dpssLength].
争论
输入参数
# timeHalfBW — 带宽一半的时间乘积
+
传:[正标量]
Details
时间乘以带宽一半的乘积,设为正标量数。 这个论点应该更小 [参数:seqLength]/2.
| 数据类型 |
|
# numSeq — 序列数
+
通过:[正整数] | 传递:[双元向量]
Details
返回的序列数,指定为正整数或双元素向量。 如果指定 n.数字,数字 作为一个双元向量,Slepyan的输出序列将从 数字(1) 以前 数字(2).
| 数据类型 |
|
输出参数
# dpsSeq — Slepyan序列(DPSS)
+
通过:[矩阵]
Details
作为矩阵返回的Slepyan序列,行数等于 [参数:seqLength],以及等于 round(2*timeHalfBW).
例子:
生成一组Slepyan序列
Details
让我们构造长度的前四个离散细长椭球序列 512. 让我们将时间的乘积设置为带宽的一半等于 2. 让我们绘制序列图并显示浓度比。
import EngeeDSP.Functions: dpss
seq_length = 512
time_halfbandwidth = 2
num_seq = 4
dps_seq, lambda = dpss(seq_length, time_halfbandwidth, num_seq)
plot(dps_seq,
title="Slepian Sequences, N = 512, NW = 2",
xlims=(0, 512),
ylims=(-0.15, 0.15),
label=["1st" "2nd" "3rd" "4th"])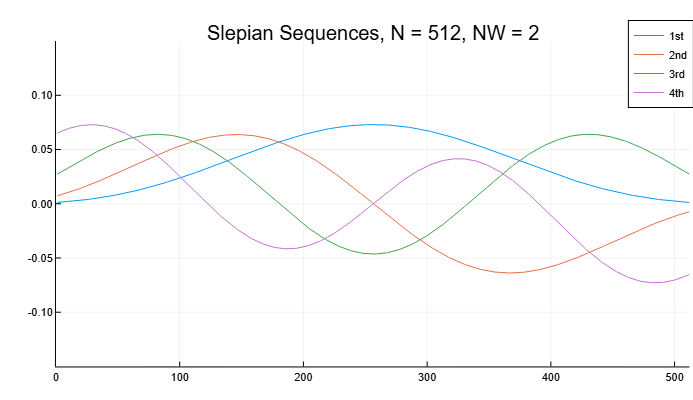
此外
离散细长球形序列
Details
离散的细长球形序列,或Slepyan序列,源自下述时频集中问题。 对于具有有限能量的所有序列 索引仅限于某些集合 ,为此序列使该比率最大化:
哪里 -采样率,以及 . 因此,该比率确定具有有限指数的哪个序列在频带中具有最大份额的能量。 . 对于具有有限索引的序列,关系必须满足不等式 . 使比率最大化的序列是第一离散细长球形序列,或Slepyan序列。 第二Slepyan序列使比率最大化并且与第一Slepyan序列正交。 Slepyan的第三序列最大化积分的比率并且与第一和第二Slepyan序列正交。 以这种方式继续,Slepyan序列形成具有有限频带的正交序列集合。