鹏飞

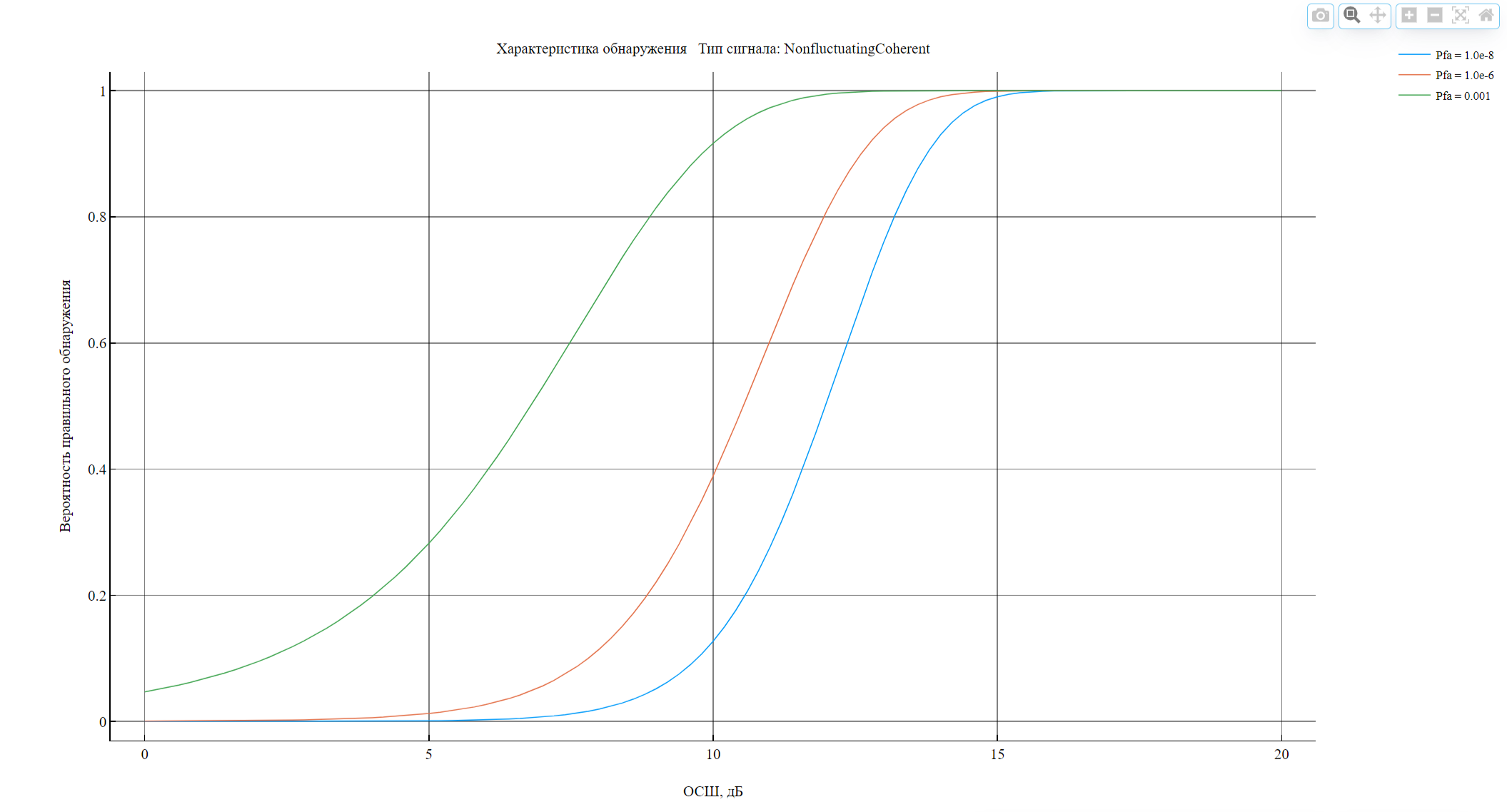
误报概率的接收器性能曲线。

资料库	`EngeePhased`。

语法

创建

可以通过以下方式调用 rocpfa 函数：

Pd,SNR=rocpfa(1e-6, "Pd&SNR")`返回单脉冲检测概率（参数 Pd）和所需的信噪比值（参数 SNR），SNR*为行或列向量 *Pfa 中的误报概率。默认情况下，对于每个误报概率，都会计算 101 个等间距 SNR 值（范围从 0 到 20 dB）的检测概率。ROC 曲线的绘制假定目标不变的相干接收机中的单脉冲。

使用方法

rocpfa(_) 绘制 ROC 曲线。

参数

输入

Pfa -. 误报概率
矢量

Details

误报概率，以行或列的矢量形式给出。

示例： [1e-8 1e-6 1e-3].

数据类型: Float64

赋值参数 Name=Value

以 Name1=Value1,…,NameN=ValueN`的形式指定可选的参数对，其中 `Name 是参数的名称，`Value`是相应的值。参数 Name=价值观必须放在其他参数之后，但参数对的顺序并不重要。

示例： MaxSNR=15,NumPoints=64,NumPulses=10。

MaxSNR - 将纳入 ROC 计算的最大信噪比 (SNR)
20（默认值） | 正标量

Details

ROC 计算中要包含的最大信噪比 (SNR)，以正标量形式指定。

数据类型: Float64

MinSNR - ROC 计算中应包含的最小信噪比 (SNR)
1e-10`（默认）｜正标量

Details

ROC 计算中包含的最小信噪比 (SNR) 指定为正标量。

数据类型: Float64

NumPoints — 计算 ROC 曲线时使用的信噪比 (SNR) 值的数量
101（默认值）` | `正整数

Details

用于计算 ROC 曲线的信噪比值个数设置为正整数。实际值介于 MinSNR 和 MaxSNR 之间。

数据类型: Float64

NumPoints - 计算 ROC 曲线时使用的信噪比 (SNR) 值的数量
101（默认值）` | `正整数

Details

用于 ROC 曲线计算的信噪比值个数设置为正整数。

实际值介于 MinSNR 和 MaxSNR 参数值之间。

数据类型: Float64

NumPulses - 积分脉冲数
1（默认值）` | `正整数

Details

用于计算 ROC 曲线的脉冲数，设置为正整数。

1 表示不进行脉冲积分。

数据类型: Float64

Details

该参数指定接收信号的类型，或者等价地指定用于计算 ROC 的概率密度函数 (PDF)。

可指定为以下值之一：

真实"。
非波动相干"。
非波动非相干`。
丝光1
`瑞典语2
`斯韦尔林
`雪糕4

数值不区分大小写。

非波动相干 "信号类型假定接收信号中的噪声是复高斯随机变量。该变量有独立的零均值实部和虚部，在零假设下，每个实部和虚部的方差为。在具有复白高斯噪声的相干接收机中的单脉冲情况下，给定误报概率时的检测概率等于：

其中，和为加法误差函数及其反函数，为无量纲信噪比 (SNR)。

数据类型: char, string

输出

Pd - 检测概率
矢量

Details

与误报概率相对应的检测概率，以向量形式返回。对于参数 Pfa 中的每个误报概率，Pd 包含一列检测概率。

数据类型: Float64

SNR - 信噪比
列向量

Details

信噪比，以列向量形式返回。

默认 SNR 值是从 0 到 20 的 101 个均匀值。

要更改 SNR 值的范围，可使用可选输入参数 MinSNR 或 MaxSNR。
要更改 SNR 值的数量，请使用可选输入参数 NumPoints。

数据类型: Float64

例子

不同误报概率 Pfa 的 ROC 曲线

Details

假设没有脉冲积分，构建 Pfa* 值为 1e-8、1e-6 和 `1e-3`的误报概率的 ROC 曲线。

Pfa = [1e-8, 1e-6, 1e-3];
rocpfa(Pfa,SignalType="NonfluctuatingCoherent")

rocpfa 1

参考资料

Richards, M. A. "雷达信号处理基础"。New York: McGraw-Hill, 2005, pp 298-336.