Rectangular QAM Demodulator Baseband
Data demodulation with rectangular QAM modulation.
blockType: RectangularQAMDemodulator
Path in the library: |
Description
Block Rectangular QAM Demodulator Baseband demodulates a signal modulated using quadrature amplitude modulation with a given order with a constellation on a rectangular grid.
| All power values assume a nominal impedance of 1 ohm. |
Ports
Entrance
In — QAM-modulated pass signal:q[<br>]scalar | vector
QAM is a modulated signal specified as a scalar or column vector.
This port remains unnamed until the Var port is enabled.
Data types: Float16, Float32, Float64, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64, Bool
Support for complex numbers: Yes
Var — noise variance
positive scalar | vector of positive values
The noise variance, specified as a positive scalar or vector of positive values. If noise dispersion or signal strength leads to calculations involving extreme positive or negative values, see the section Soft Demodulation to consider the type of demodulation solution.
Dependencies
To enable this parameter, set the Noise variance source parameter to Port.
Data types: Float64
Parameters
Main
M-ary number — modulationrass order:q[<br>]16 (default) | positive integer
The modulation order is set as a positive integer equal to two. The modulation order M determines the number of points in the signal constellation.
M must have the form 2K for some positive integer K.
The block scales the signal constellation depending on the value of the Normalization method parameter.
Output type — output type
Integer (default) | Bit
Determines whether the block will output integers or binary representations of integers.
-
If you set the Output type parameter to
Integer, the block outputs integers in the range [0, (M -1)] for each character. M is the modulation order (M-ary number). -
If you set the Output type parameter to
Bitand the Decision type parameter toHard decision, then for each character, the block outputs a group of K bits called a binary word. K=log2(M). -
If you set the Output type parameter to
Bitand the Decision type parameter toLog–likelihood ratioorApproximate log-likelihood ratio, the block outputs a bitwise LLR (communication loss signal) or approximate LLR, respectively.
Decision type — demodulation decision type:q[<br>]Hard decision (default) | Log-likelihood ratio | Approximate log-likelihood ratio
The type of demodulation solution specified as Hard decision', `Log-likelihood ratio or `Approximate log-likelihood ratio'.
Dependencies
This parameter appears when the Output type parameter is set to Bit1.
Noise variance source — noise variance source
Dialog (default) | Port
The source of the noise dispersion, specified as Dialog or `Port'.
-
When selecting
Dialog, the Noise variance parameter must be used to set the noise variance. -
When selecting
Port, the Var port must be used to set the noise dispersion.
Dependencies
To enable this parameter, set the Decision type parameter to Approximate log-likelihood ratio or `Log-likelihood ratio'.
Noise variance — noise variance
1 (default) | positive scalar | vector of positive values
The noise variance is given as a positive scalar or vector of positive values.
When setting the Noise variance parameter as a scalar, this value is used for all elements of the input signal.
When setting the Noise variance parameter as a vector, the length of the vector must be equal to the number of columns in the input signal. Each element of the noise dispersion vector is applied to the corresponding column of the input signal.
This parameter is configured in normal mode, accelerator mode, and fast accelerator mode.
The exact LLR algorithm calculates exponentials using finite precision arithmetic. For calculations with very large positive or negative values, the exact LLR algorithm gives:
-
Infor `-Inf' if the noise dispersion is very large. -
NaNif the noise dispersion and signal strength are very small.
The approximate LLR algorithm does not calculate exponents. You can avoid the results of Inf, -Inf and NaN by using an approximate LLR algorithm.
Dependencies
To enable this parameter, set the Decision Type parameter to Log-likelihood ratio or Approximate log-likelihood ratio and set the Noise variance source parameter to Dialog.
Constellation ordering — the order in which characters are displayed is as follows:q[<br>]Binary (default) | Gray | User-defined
The order in which characters are displayed is set as Binary, Gray, or `User-defined'.
The Constellation ordering parameter defines how the block maps each character to a group of output bits or an integer.
Constellation mapping — user-defined mapping of constellations
[0:15] (default) | vector
The constellation display you define, defined as an M element containing unique integer values in the range [0, (M -1)].
The first element of this vector corresponds to the uppermost left point of the constellation, and the subsequent elements follow the columns from left to right. The last element corresponds to the lowest and rightmost point.
Dependencies
To enable this parameter, set the Constellation ordering parameter to User-defined.
Normalization method — scaling method for the constellation
Min. distance between symbols (default) | Average Power | Peak Power
The constellation scaling method, defined as the minimum distance between symbols, average power, or peak power.
Minimum distance — the distance between the two closest points of the constellation
2 (default)| positive scalar
The distance between the two closest points of the constellation, given as a positive scalar.
Dependencies
To enable this parameter, set the Normalization method parameter to Min. distance between symbols.
Average power, referenced to 1 ohm (W) — average pass power:Q[<br>]1 (default)| positive scalar
The average power of the symbols in the constellation in watts, given as a positive scalar. The power values assume a nominal impedance of 1 ohm.
The unit of measurement is watt.
Dependencies
To enable this parameter, set the Normalization method parameter to Average Power.
Peak power, referred to 1 ohm (W) — Peak power
1 (default)| positive scalar
The maximum power of symbols in a constellation, given as a positive scalar. The power values assume a nominal impedance of 1 ohm.
The unit of measurement is watt.
Dependencies
To enable this parameter, set the Normalization method parameter to Peak Power.
Phase offset (rad) — rotation of the signal constellation
0 (default) | numeric scalar
The rotation of the signal constellation, specified as a numeric scalar.
The unit of measurement is radian.
Algorithms
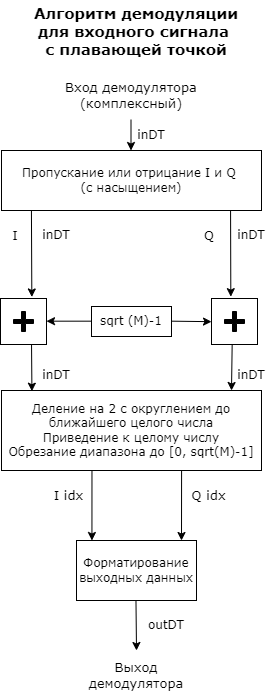
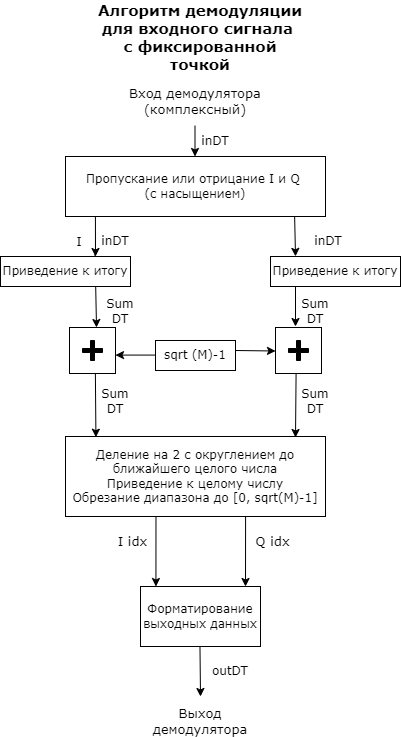
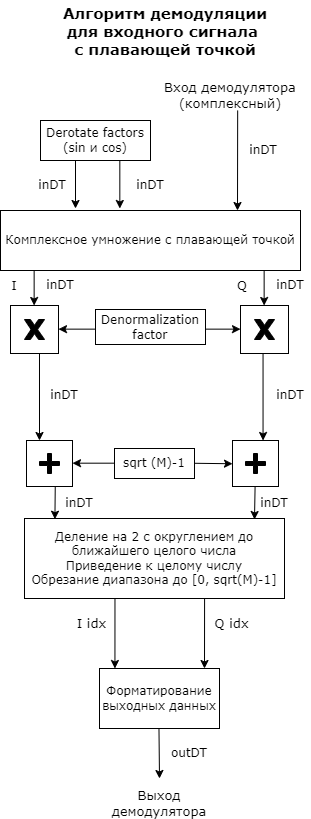
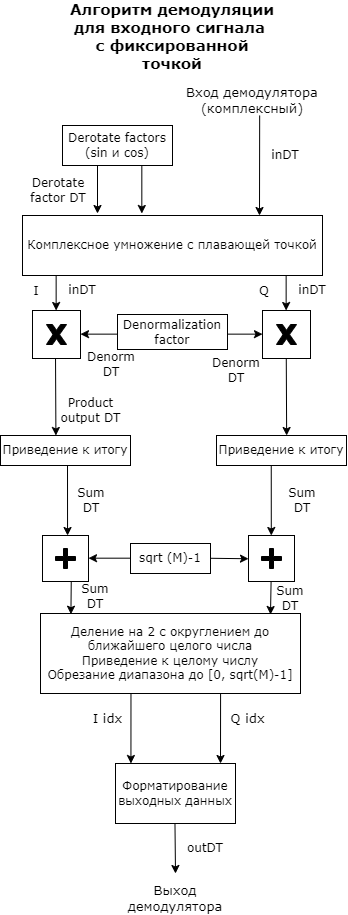
Hard QAM signal demodulation
The demodulator algorithm converts the obtained values of the input signal constellations into M-dimensional integer indexes of the symbols I and Q in the range [ ], and then converts these demodulated character indexes into formatted output values. M is the value of the M-ary number parameter.
The calculation of the integer symbolic index is performed by derotating and scaling the complex constellation of the input signal (possibly with noise) by the derotation coefficient and the denormalization coefficient, respectively. These coefficients are determined based on the phase shift (rad), the normalization method, and the corresponding parameters. These derated and denormalized values are added to to put them in an approximate range [ ]. – this is the added value of noise.
The resulting values are then scaled by dividing by two (or, equivalently, shifting right by one bit for fixed-point operations) to get a range of approximately [ ] for I and Q.
Noisy index values are rounded to the nearest integer and trimmed using saturation, and then converted to integer values of characters in the range. ].
Finally, based on other block parameters, the integer index is mapped to a character value, which is formatted and converted to the selected output type.
These figures show flowcharts for the operation of floating-point and fixed-point algorithms.
Floating point diagrams are used when the input data type is double or single.
Fixed-point diagrams are used when the input signal is a signed fixed-point data type. The diagram is simplified if the phase shift (rad) is a multiple of or the derived denormalization coefficient is 1.
Signal conversion schemes with trivial phase shift and denormalization coefficient equal to 1.
|
|
Signal conversion schemes with non-trivial phase shift and uneven denormalization coefficient.
|
|
Software demodulation of the QAM signal
Two log likelihood ratio (LLR) algorithms with smooth decision making are available for software demodulation: exact LLR and approximate LLR.
The exact LLR algorithm is more accurate, but the execution speed is lower than that of the approximate LLR algorithm.
The exact LLR algorithm calculates exponentials using finite precision arithmetic. For calculations involving very large positive or negative values, the exact LLR algorithm gives the result:
Inf or -Inf if the noise variance is very large.,
NaN if the noise dispersion and signal strength are very small.
The approximate LLR algorithm does not calculate exponents. You can avoid the results of Inf, -Inf and NaN by using the approximate LLR algorithm.
|
Constellation size and scaling
The set of signals contains M points, where M is the parameter M-ary number.
M should have the form for some positive integer K.
The block scales the signal constellation depending on the value set for the Normalization method parameter.
The following table lists the possible scaling conditions.
| The value of the Normalization method parameter | Zoom condition |
|---|---|
|
The nearest pair of points in the constellation is separated depending on the value of the Minimum distance parameter. |
|
The average power of the symbols in the constellation is the parameter Average power, referred to 1 ohm (W). |
|
The maximum power of the symbols in the constellation is the Peak power parameter, referred to 1 ohm (W) |