What is system modelling
In this article, we will look at the concepts and terms that are used in the Engee environment.
System
A System is a group of interdependent physical and functional parts whose characteristics are firstly measurable and secondly time-varying.
For example, a car can be considered as a system consisting of several parts. Examples of characteristics are linear speed and wheel speed.

System component
A System component is a part of a system that interacts with other parts. The interactions between components determine the structure and behaviour of the system.
For example, the cruise control module is a system component in a vehicle system. The microcontroller and associated hardware determine the structure, and the software algorithm for speed control determines the behaviour.

Model
A Model is a mathematical description of a system derived either from physical laws or from experimental data. A model typically uses a set of variables related by differential and algebraic equations and the coefficients of these equations.
Let us return to the simplified car model.
Variables:
-
u(t)- force (N) acting on the car; -
v(t)- speed of the car (m/s). Parameters: -
b- drag coefficient (N-s/m); -
m- mass (kg).
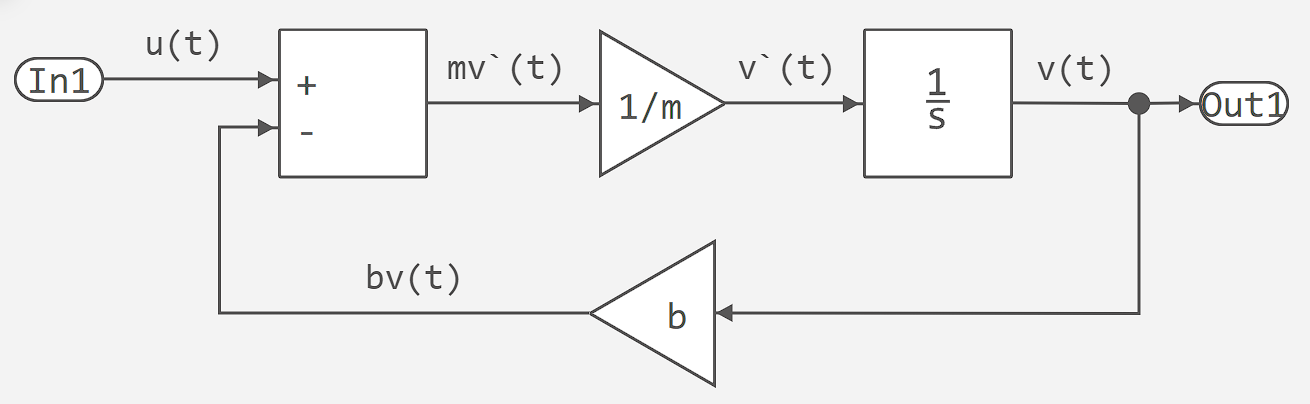
Let us represent the car as a continuous system. Then the changes in all variables can be fully described by a system of differential equations defined for all values of time. The velocity of the vehicle v(t) and its acceleration v'(t) are related by the following first order differential equation.
It is possible to create an Engee model for this equation. To do this, you need to transfer the appropriate blocks into the model, set their parameters and, using signal lines, connect them to each other. The following Engee block diagram realises the above differential equation:
Differential-algebraic equations
Some systems of equations contain additional constraints that include an independent variable and a state vector in addition to the differential equations. Such systems are called differential-algebraic equations (DAEs).
The term algebraic refers to equations that do not contain derivatives.
In Engee models, algebraic loops, or loops, are algebraic constraints. Models with algebraic loops define a system of differential-algebraic equations.
For example,
represents the system of differential-algebraic equations realised in the following Engee model: