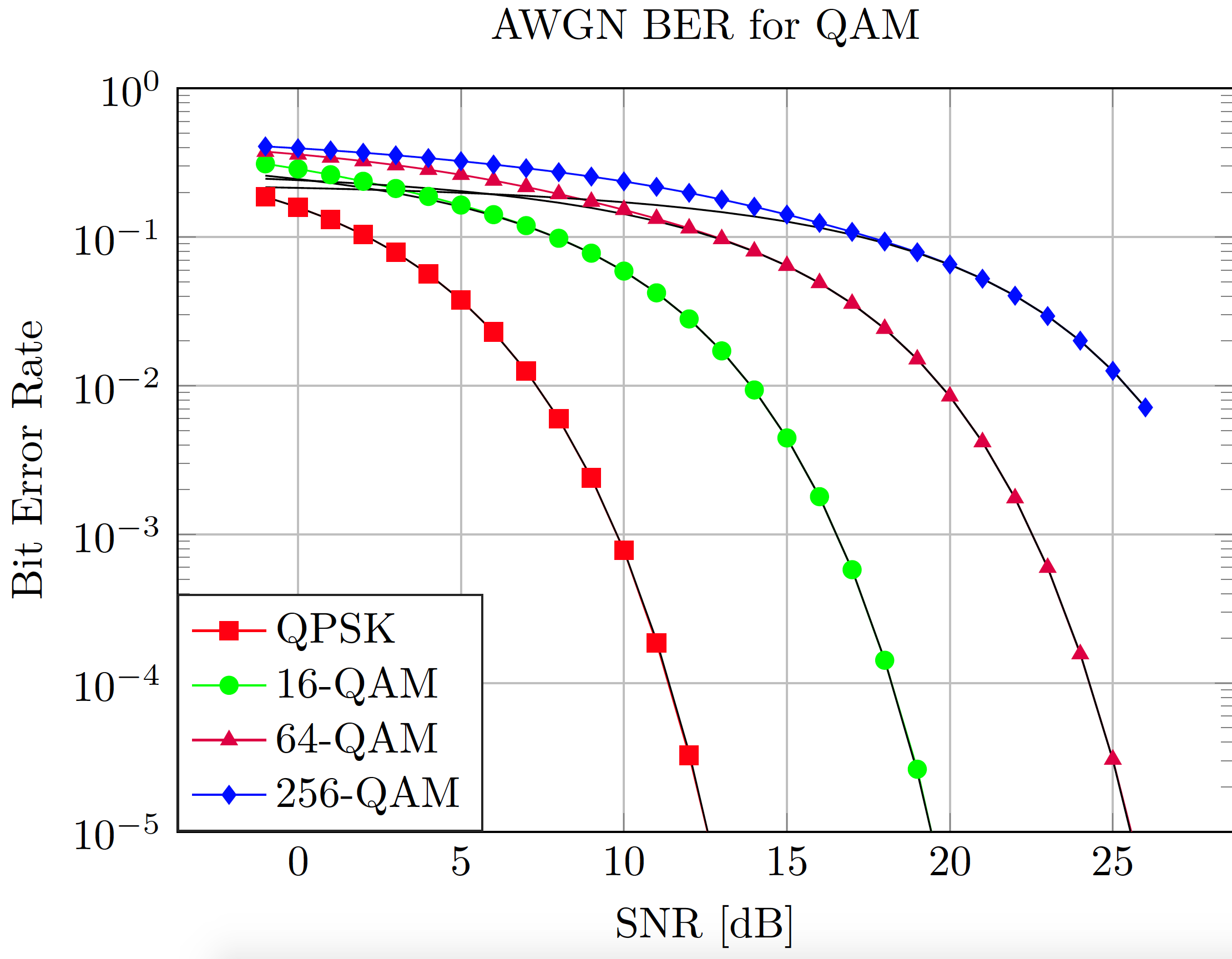
Compute the theoretical BER for AWGN channel and various constellation size
Based on the previous skeleton, we can now compute an iterative testbench to compute the Bit Error Rate for various constellation size, and compare the simulation with the theory. As a gentle reminder, the theoretical bit error rate can be approximated as
First of all let’s call the modules
using DigitalComm using PGFPlotsX
We define first the main monte-carlo function that compute an elementary Tx-Rx link, and returns the number of error and number of bit computed (to be accumulated)
function monteCarlo(snr,mcs,nbSymb) # Number of bits nbBits = nbSymb * Int(log2(mcs)); # --- Binary sequence generation bitSeq = genBitSequence(nbBits); # --- QPSK mapping qamSeq = bitMappingQAM(mcs,bitSeq); # ---------------------------------------------------- # --- Channel # ---------------------------------------------------- # --- AWGN # Theoretical power is 1 (normalized constellation) qamNoise, = addNoise(qamSeq,snr,1); # ---------------------------------------------------- # --- Rx Stage: SRRC # ---------------------------------------------------- # --- Binary demapper bitDec = bitDemappingQAM(mcs,qamNoise); # --- Error counter nbE = sum(xor.(bitDec,bitSeq)); # --- Return Error and bits return (nbE,nbBits); end
A function to plot the BER versus the SNR, for different mcs and compare to theory
function doPlot(snrVect,ber,qamVect)
a = 0;
@pgf a = Axis({
ymode = "log",
height ="3in",
width ="4in",
grid,
xlabel = "SNR [dB]",
ylabel = "Bit Error Rate ",
ymax = 1,
ymin = 10.0^(-5),
title = "AWGN BER for QAM",
legend_style="{at={(0,0)},anchor=south west,legend cell align=left,align=left,draw=white!15!black}"
},
Plot({color="red",mark="square*"},Table([snrVect,ber[1,:]])),
LegendEntry("QPSK"),
Plot({color="green",mark="*"},Table([snrVect,ber[2,:]])),
LegendEntry("16-QAM"),
Plot({color="purple",mark="triangle*"},Table([snrVect,ber[3,:]])),
LegendEntry("64-QAM"),
Plot({color="blue",mark="diamond*"},Table([snrVect,ber[4,:]])),
LegendEntry("256-QAM"),
);
# --- Adding theoretical curve
snrLin = (10.0).^(snrVect/10)
for qamScheme = qamVect
ebNo = snrLin / log2(qamScheme);
# This approximation is only valid for high SNR (one symbol error is converted to one bit error with Gray coding).
berTheo = 4 * ( 1 - 1 / sqrt(qamScheme)) / log2(qamScheme) * qFunc.(sqrt.( 2*ebNo * 3 * log2(qamScheme) / (2*(qamScheme-1) )));
@pgf push!(a,Plot({color="black"},Table([snrVect,berTheo])));
end
display(a);
end
Then, the main routine to compute the BER for a given number of iterations and a range of SNR
function main() # --- Parameters nbIt = 10000; # Number of iterations nbSymb = 1024; # Number of symbols per iterations mcs = [4,16,64,256]; # Constellation size snrRange = (-1:26); # SNR, expressed in dB # --- Init performance metrics nbSNR = length(snrRange); ber = zeros(Float64,length(mcs),nbSNR); for iMcs = 1 : 1 : length(mcs) for iSNR = 1 : 1 : nbSNR # --- Create BER counters nbE = 0; nbB = 0; for iN = 1 : 1 : nbIt # --- Elementary MC call # Corresponds to a given SNR and a given iteration # As we are ergodic in AWGN, it is only nbSymb*nbIt that matters for BER computation (a,b) = monteCarlo(snrRange[iSNR],mcs[iMcs],nbSymb); # --- Update counters nbE += a; # Increment errors nbB += b; # Increment bit counters end ber[iMcs,iSNR] = nbE / nbB; end end # --- Plotting routine doPlot(snrRange,ber,mcs); end
The output plot is the following, showing adequacy between theory and practise for high SNR (the theoretical curve is under the assumption that one symbol error leads to one erroneous bit (gray coding) which is true only with intermediate noise levels).