angle
Фазовый угол.
| Библиотека |
|
Аргументы
Входные аргументы
#
z —
входные данные
скаляр | вектор | матрица | многомерный массив
Details
Входные данные, заданные как скаляр, вектор, матрица или многомерный массив. Если элементы z — неотрицательные вещественные числа, то angle возвращает 0. Если элементы z — отрицательные вещественные числа, то angle возвращает π.
| Типы данных |
|
| Поддержка комплексных чисел |
Да |
Выходные аргументы
#
theta —
выходные фазовые углы
скаляр | вектор | матрица | многомерный массив
Details
Выходные углы, возвращаемые в виде скаляра, вектора, матрицы или многомерного массива. Углы в theta таковы, что z = abs(z).*exp(i*theta).
Примеры
Модуль и фаза комплексного числа
Details
Создадим комплексное число z и вычислим его модуль r и фазу theta.
import EngeeDSP.Functions: angle
import EngeeDSP.Functions: abs
z = 2 * exp(im * 0.5)
r = abs(z)
theta = angle(z)
println("z=",z)
println("r=",r)
println("theta=",theta)z=1.7551651237807455 + 0.958851077208406im
r=2.0
theta=0.5Фаза БПФ
Details
Создадим сигнал, состоящий из двух синусоид с частотами 15 Гц и 40 Гц. Первая синусоида имеет фазу −π/4, а вторая — π/2. Дискретизируем сигнал с частотой 100 Гц в течение одной секунды.
import EngeeDSP.Functions: angle, fft, fftshift
fs = 100
t = 0:1/fs:1-1/fs
x = cos.(2*pi*15*t .- pi/4) .- sin.(2*pi*40*t);Вычислим преобразование Фурье сигнала. Построим график зависимости модуля преобразования Фурье от частоты.
y = fft(x)
z = fftshift(y)
ly = length(y)
f = (-ly/2:ly/2-1)/ly*fs;
plot(f, abs(z), xlabel="Frequency (Hz)", ylabel="|y|")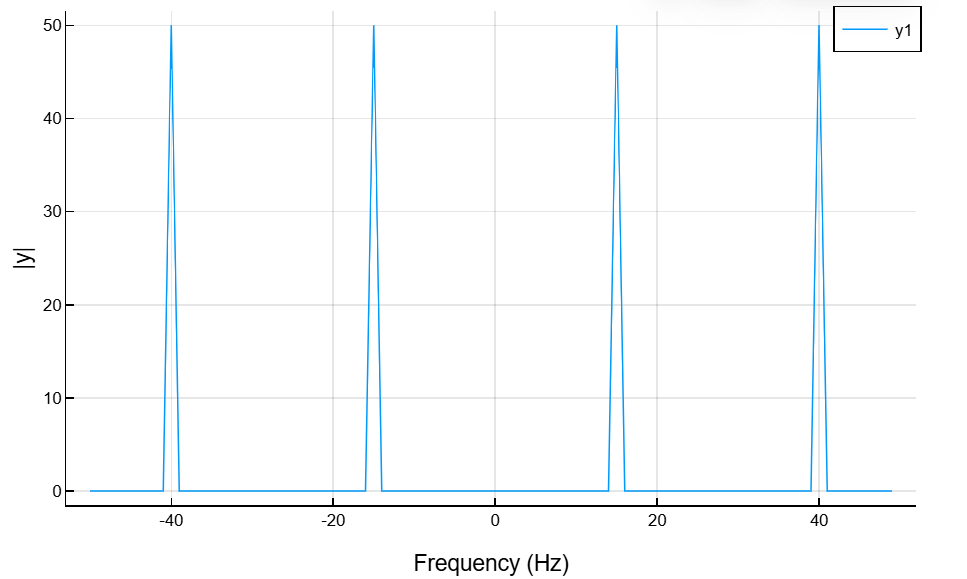
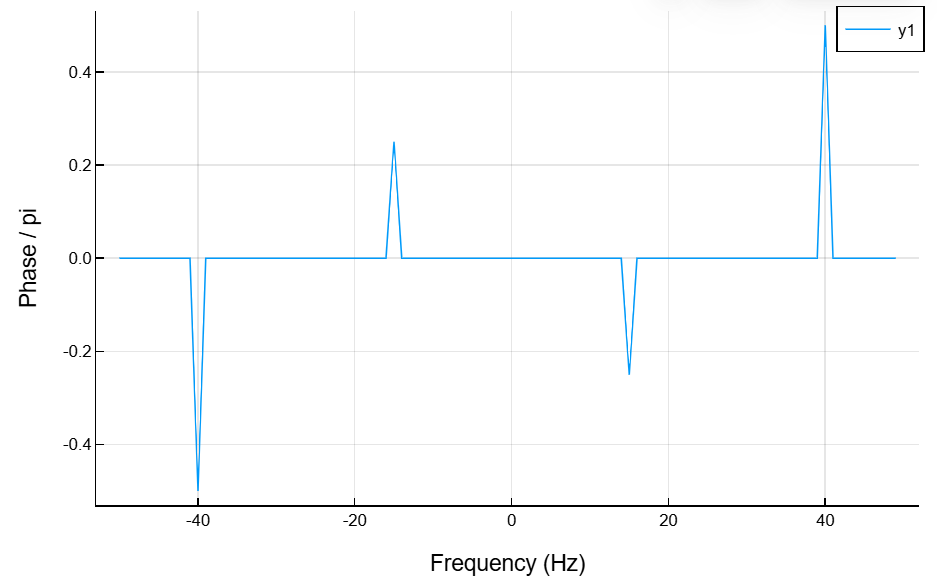
Вычислим фазу преобразования Фурье, удалив значения преобразования малой амплитуды. Построим график зависимости фазы от частоты.
tol = 1e-6
z[abs(z) .< tol] .= 0
theta = angle(z)
plot(f, theta/pi, xlabel="Frequency (Hz)", ylabel="Phase / pi")