spline
Интерполяция данных кубическим сплайном.
| Библиотека |
|
Аргументы
Входные аргументы
#
x —
координаты x
вектор
Details
Координаты x, заданные как вектор. Вектор x определяет точки, в которых заданы данные y. Элементы x должны быть уникальными.
Кубическая сплайн-интерполяция требует не менее 4 точек. При наличии 2 или 3 точек применяется линейная или квадратичная интерполяция соответственно.
| Типы данных |
|
#
y —
значение функции при заданных координатах x
вектор | матрица | массив
Details
Значения функции в координатах x, заданные как числовой вектор, матрица или массив. Аргументы x и y обычно имеют одинаковую длину, но y также может иметь ровно на два элемента больше, чем x, для задания конечных наклонов.
Если y — матрица или массив, то значения в последнем измерении, y(:,…,:,j), берутся в качестве значений для сопоставления с x. В этом случае последнее измерение y должно иметь ту же длину, что и x, или иметь ровно на два элемента больше.
Конечные наклоны кубического сплайна подчиняются следующим правилам:
-
Если
xиy— векторы одинакового размера, то используются условия «не узел». -
Если
xилиy— скаляр, то он расширяется до той же длины, что и другой, и используются условия «не узел». -
Если
y— вектор, содержащий на два элемента больше значений, чемx, то сплайн использует первое и последнее значения вyв качестве конечных наклонов кубического сплайна. Например, еслиy— вектор, то: -
Аналогично, если
y— матрица или -мерный массив с размеромsize(y,N), равнымlength(x)+2, то:
| Типы данных |
|
Выходные аргументы
#
s —
интерполированные значения в точках запроса
скаляр | вектор | матрица | массив
Details
Интерполированные значения в точках запроса, возвращаемые в виде скаляра, вектора, матрицы или массива.
#
pp —
кусочный полином
структура
Details
Кусочный полином, возвращаемый в виде структуры. Структура содержит поля, приведенные в таблице.
| Поле | Описание |
|---|---|
|
|
|
Вектор длины со строго возрастающими элементами, представляющими начало и конец каждого из интервалов |
|
Матрица размером на , в которой каждая строка |
|
Количество частей |
|
Степень полиномов |
|
Размерность цели |
Поскольку коэффициенты полиномов в coefs являются локальными коэффициентами для каждого интервала, необходимо вычесть нижнюю границу соответствующего интервала узла, чтобы использовать коэффициенты в обычном полиномиальном уравнении. Другими словами, для коэффициентов на интервале соответствующий полином равен:
Примеры
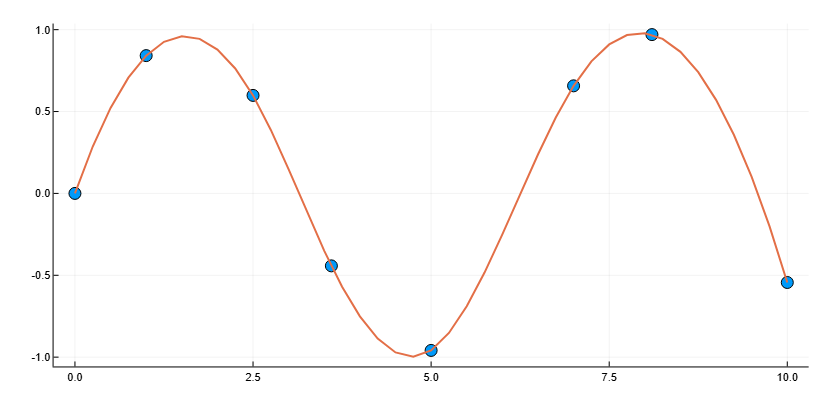
Сплайн-интерполяция синусоидальных данных
Details
Используем spline для интерполяции синусоидальной кривой по неравномерно расположенным точкам выборки.
import EngeeDSP.Functions: spline
x = [0, 1, 2.5, 3.6, 5, 7, 8.1, 10]
y = sin.(x)
xx = 0:0.25:10
yy = spline(x, y, xx)
plot(x, y, seriestype=:scatter, markersize=6, legend=false)
plot!(xx, yy, linewidth=2, legend=false)