npwgnthresh
Порог отношения сигнал/шум (SNR) для обнаружения сигнала в белом гауссовском шуме.
| Библиотека |
|
Синтаксис
Вызов функции
Вызов функции npwgnthresh возможен следующими способами:
-
snrthresh = npwgnthresh(pfa)вычисляет порог отношения сигнал/шум (SNR) в дБ для обнаружения детерминированного сигнала в белом гауссовом шуме. При детектировании используется решающее правило Неймана-Пирсона (NP) для достижения заданной вероятности ложной тревоги, аргумент pfa. Эта функция использует квадратичный детектор. -
snrthresh = npwgnthresh(pfa,numpulses)задает аргумент numpulses как количество импульсов, используемых при интегрировании импульсов. -
snrthresh = npwgnthresh(pfa,numpulses,dettype)задает тип данных в качестве типа обнаружения. При некогерентном обнаружении используется прямоугольный детектор. -
snrthresh = npwgnthresh(pfa,numpulses,dettype,outscale)задает масштаб вывода.
Аргументы
Вход
pfa —
вероятность ложной тревоги
скаляр в диапазоне (0, 1)
Details
Вероятность ложной тревоги, заданная в виде скаляра в диапазоне (0, 1).
Типы данных: Float64
numpulses —
количество импульсов
1 (по умолчанию) | целое положительное число
Details
Количество импульсов, используемых в интегрировании, заданное как положительное целое число.
Типы данных: Float64
dettype —
тип импульсного интегрирования
noncoherent (по умолчанию) | coherent | real
Details
Определяет тип импульсного интегрирования, используемого в правиле принятия решений NP.
Задается как coherent, noncoherent или real.
-
coherentиспользует информацию о величине и фазе комплексных выборок. -
noncoherentиспользует квадратичные величины. -
realиспользует вещественные выборки.
Типы данных: char, string
outscale —
масштаб выходного значения
db (по умолчанию) | linear
Details
Масштаб выходного значения, заданный как db или linear.
Если для аргумента outscale задано значение linear, возвращаемый порог представляет собой амплитуду.
Типы данных: char, string
Выход
snrthresh —
порог обнаружения
скаляр
Details
Порог обнаружения, заданный в виде скаляра.
Порог обнаружения выражается в отношении сигнал/шум (SNR) в дБ или в линейных единицах, если для аргумента outscale задано значение linear.
Связь между линейным порогом ( ) и порогом в дБ ( ) выражается как:
Примеры
Линейный порог обнаружения в зависимости от количества импульсов
Details
Постройте график зависимости линейного порога обнаружения от количества импульсов для вещественных и комплексных данных. В каждом случае порог устанавливается с вероятностью ложной тревоги (Pfa) 0.001.
Вычислите порог обнаружения для 1-10 импульсов вещественного и комплексного шума.
Npulses = 10
Pfa = 1e-3
snrreal = npwgnthresh.(Pfa, 1:Npulses, "real", "linear")
snrcoh = npwgnthresh.(Pfa, 1:Npulses, "coherent", "linear")
plot([snrreal snrcoh], label = ["Real data with integration" "Complex data with coherent integration"], xlabel = "Number of Pulses", ylabel = "Detection Threshold", title = "Linear Detection Threshold for P_FA = $Pfa", marker = :circle, legendposition = :bottomright)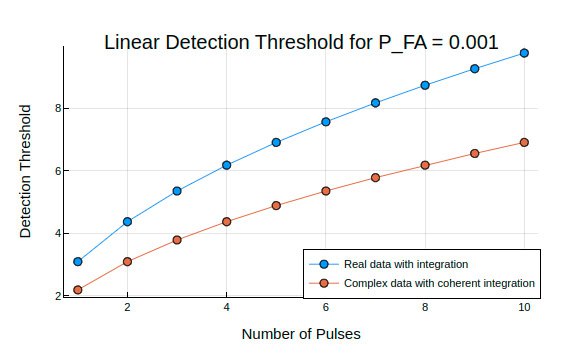
Дополнительно
Порог отношения сигнал/шум (SNR) при обнаружении сигнала
Details
Выход функции npwgnthresh определяет порог обнаружения, необходимый для достижения определенной вероятности ложной тревоги (pfa).
Порог увеличивается, если в приемнике используется интегрирование импульсов. Этот порог не является SNR одиночного сигнала, который используется в качестве входа функции rocsnr или выхода функций rocpfa, albersheim и shnidman.
Для любого фиксированного значения вероятности ложной тревоги (pfa) вы можете уменьшить отношение сигнал/шум одиночной выборки, необходимый для достижения определенной вероятности обнаружения (pd), если в приемнике используется интегрирование импульсов.
Обнаружение вещественных значений сигнала в белом гауссовском шуме
Details
Эта функция предназначена для обнаружения ненулевого среднего значения в последовательности гауссовских случайных величин. Функция предполагает, что случайные величины являются независимыми и одинаково распределенными, с нулевым средним значением.
Линейный порог обнаружения для детектора NP равен:
Этот порог также может быть выражен как отношение сигнал/шум в дБ:
В этих уравнениях
-
– дисперсия последовательности белого гауссовского шума;
-
– количество сигналов;
-
– обратная функция дополнительной ошибки;
-
– вероятность ложной тревоги.
Если вероятность ложной тревоги (pfa) больше или равна 1/2, формула для порога обнаружения, как отношение сигнал/шум, недействительна, поскольку меньше или равна нулю для значений своего аргумента, больших или равных единице. В этом случае используйте линейный вывод функции, вызванной аргументом outscale со значением linear.
|
Обнаружение комплекснных значений сигнала в белом гауссовском шуме (когерентные выборки)
Details
Дя функции npwgnthresh делаются следующие предположения:
-
Дисперсия комплексной гауссовской случайной величины делится поровну между действительной и мнимой частями.
-
Действительная и мнимая части некоррелированы. Согласно этим предположениям, порог линейного обнаружения для детектора NP составляет:
и выраженное как отношение сигнал/шум в дБ:
Если вероятность ложной тревоги (pfa) больше или равна 1/2, формула для порога обнаружения, как отношение сигнал/шум, недействительна, поскольку меньше или равна нулю для значений своего аргумента, больших или равных единице. В этом случае используйте линейный вывод функции, вызванной аргументом outscale со значением linear.
|
Обнаружение некогерентных значений сигнала в белом гауссовском шуме
Details
Для некогерентных сигналов в белом гауссовском шуме обнаружение ненулевого среднего приводит к детектору квадратичного закона. Подробный вывод см. в Richards, M. A. "Fundamentals of Radar Signal Processing.", стр. 324-329.
Линейный порог обнаружения для некогерентного детектора NP составляет:
Пороговое значение, выраженное в виде отношения сигнал/шум в дБ, составляет:
где - обратная нижняя неполная гамма-функция, – вероятность ложной тревоги, а – количество импульсов.
Смотрите также
-
Kay, S. M. "Fundamentals of Statistical Signal Processing: Detection Theory. Upper Saddle River", NJ: Prentice Hall, 1998.
-
Richards, M. A. "Fundamentals of Radar Signal Processing." New York: McGraw-Hill, 2005.