rangeangle
Расчет дальности и угла наклона.
| Библиотека |
|
Описание
Функция rangeangle определяет длину и направление пути распространения сигнала от точки-источника или набора точек-источников до опорной точки.
Функция поддерживает две модели распространения – модель свободного пространства и двухлучевую модель.
-
Модель свободного пространства представляет собой траекторию прямой видимости от исходной точки до контрольной точки.
-
Двухлучевая модель генерирует две траектории. Первая траектория соответствует траектории в свободном пространстве. Вторая траектория представляет собой траекторию, отраженную от граничной плоскости при . Направления траектории определяются либо относительно глобальной системы координат в контрольной точке, либо относительно локальной системы координат в контрольной точке. Расстояния и углы в контрольной точке не зависят от того, в каком направлении сигнал распространяется по траектории.
Синтаксис
Вызов функции
Вызов функции rangeangle возможен следующими способами:
-
rng,ang = rangeangle(pos)возвращает длину пути распространения (аргумент rng) и углы направления (аргумент and) пути прохождения сигнала от исходной точки или набора исходных точек (аргумент pos) до начала координат в глобальной системе координат. Углами направления являются азимут и угол возвышения относительно осей глобальных координат в начале координат. Сигналы проходят по траектории прямой видимости от исходной точки к началу координат. Траектория прямой видимости соответствует геометрической прямой линии между точками. -
rng,ang = rangeangle(pos,refpos)также задает опорную точку или набор опорных точек (аргумент refpos). Аргумент rng теперь содержит длину пути распространения от исходных точек до опорных точек. Углы направления – это азимут и высота по отношению к глобальным координатным осям в опорных точках. Можно указать несколько точек и несколько опорных точек. -
rng,ang = rangeangle(pos,refpos,refaxes)также задает локальные оси системы координат (аргумент refaxes) в опорных точках. Дирекционные углы – это азимут и высота по отношению к локальным осям координат с центром в точке refpos. -
rng,ang = rangeangle(_,model)также задает модель распространения. Если модель имеет значениеfreespace, сигнал распространяется по траектории прямой видимости от точки источника до точки приема. Если модель имеет значениеtwo-ray, сигнал распространяется по двум путям от точки источника до точки приема. Первый путь – это путь прямой видимости. Второй путь – отражающий. В этом случае функция возвращает расстояния и углы для двух путей для каждой точки источника и соответствующей опорной точки.
Аргументы
Вход
pos —
положение исходной точки
вещественный вектор 3 на 1 | вещественная матрица 3 на N
Details
Положение исходной точки в метрах, заданное в виде вещественного вектора 3 на 1 или вещественной матрицы 3 на . Матрица представляет несколько исходных точек. Столбцы содержат декартовы координаты точек в форме [x;y;z].
-
Если pos – это матрица 3 на , нужно указать входной аргумент refpos как матрицу 3 на для опорных точек .
-
Если все опорные точки идентичны, можно указать аргумент refpos как вектор 3 на 1.
Пример: [1000;2000;50]
Типы данных: Float64
refpos —
положение опорной точки
[0;0;0] (по умолчанию) | вещественный вектор 3 на 1 | вещественная матрица 3 на N
Details
Положение опорной точки в метрах, заданное в виде вещественного вектора 3 на 1 или вещественной матрицы 3 на . Матрица представляет несколько опорных точек. Столбцы содержат декартовы координаты точек в форме [x;y;z].
-
Если refpos – это матрица 3 на , нужно указать аргумент pos как матрицу 3 на для исходных точек .
-
Если все исходные точки идентичны, можно задать pos как вектор 3 на 1.
Пример: [100;100;10]
Типы данных: Float64
refaxes —
оси локальной системы координат
[1 0 0;0 1 0;0 0 1] (по умолчанию) | вещественная матрица 3 на 3 | вещественный массив 3 на 3 на N
Details
Оси локальной системы координат, заданные в виде вещественной матрицы 3 на 3 или массива 3 на 3 на .
Для массива каждая страница соответствует локальной оси координат в каждой точке отсчета.
Столбцы в аргументе refaxes задают направление осей координат локальной системы координат в декартовых координатах. должно совпадать с количеством столбцов в аргументе pos или refpos, если эти размерности больше единицы.
Пример: rotz(45)
Типы данных: Float64
model —
модель распространения
freespace (по умолчанию) | two-ray
Details
Модель распространения, указанная как freespace или two-ray.
-
Если задано значение
freespace, вызывается модель распространения в свободном пространстве. -
Если задано значение
two-ray, вызывается двулучевая модель распространения.
Типы данных: char, string
Выход
rng —
диапазон распространения
вещественный вектор 1 на N | вещественный вектор 1 на 2N
Details
Дальность распространения в метрах, возвращается в виде вектора с вещественным значением 1 на или вектора с вещественным значением 1 на 2 .
-
Если у аргумента model задано значение
freespace, размерность rng равна 1 на . Диапазон распространения – это длина прямого пути от позиции, определенной в аргументе pos, до соответствующей позиции, определенной в аргумененте refpos. -
Если у аргумента model задано значение
two-ray, rng содержит диапазоны для прямого и отраженного пути. Альтернативные столбцы rng относятся к пути прямой видимости и отраженному пути, соответственно, для одной и той же пары источник – опорная точка.
ang —
азимут и углы возвышения
вещественная матрица 2 на N | вещественная матрица 2 на 2N
Details
Азимут и углы возвышения в градусах, возвращаемые в виде матрицы 2 на или матрицы 2 на 2 . Каждый столбец представляет угол направления в форме [azimuth;elevation].
-
Если у аргумента model задано значение
freespace, аргумент ang является матрицей 2 на и представляет собой угол пути от исходной точки до опорной точки. -
Если у аргумента model задано значение
two-ray, аргумент ang – это матрица 2 на 2 . Альтернативные столбцы ang относятся к пути прямой видимости и отраженному пути, соответственно.
Примеры
Расчет дальности и угла наклона
Details
Вычислите дальность и угол наклона цели, расположенной на расстоянии (1000,2000,50) метров от начала координат.
TargetLoc = [1000;2000;50];
tgtrng,tgtang = rangeangle(TargetLoc)Расчет диапазона и угла наклона относительно местных координат
Details
Вычислите дальность и угол до цели, расположенной на расстоянии (1000,2000,50) метров, но относительно начала координат в локальной системе координат на расстоянии (100,100,10) метров. Выберите локальную систему отсчета координат, которая повернута вокруг оси на 45° относительно глобальных осей координат.
targetpos = [1000;2000;50];
origin = [100;100;10];
refaxes = [1/sqrt(2) -1/sqrt(2) 0; 1/sqrt(2) 1/sqrt(2) 0; 0 0 1];
tgtrng,tgtang = rangeangle(targetpos,origin,refaxes)Дополнительно
Углы в локальной и глобальной системах координат
Details
Функция rangeangle возвращает расстояние до траектории и углы траектории в глобальной или локальной системе координат.
Каждая антенна или акустический элемент и антенная решетка имеют диаграмму направленности, которая выражается в локальных угловых координатах азимута и высоты.
Когда элемент или антенная решетка перемещается или вращается, диаграмма усиления переносится вместе с ней. Чтобы определить силу сигнала, вы должны знать угол, который составляет путь сигнала по отношению к локальным угловым координатам элемента или антенной решетки. По умолчанию функция rangeangle определяет угол, который путь сигнала составляет по отношению к глобальным координатам.
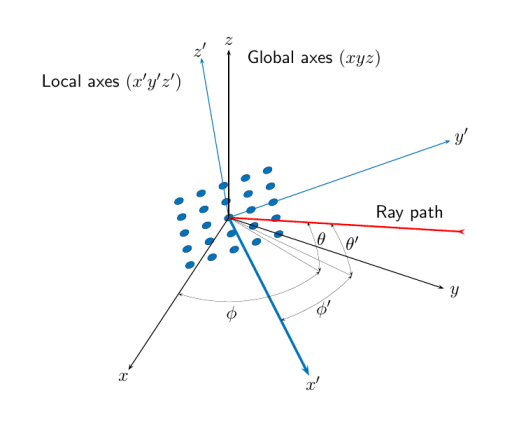
Если добавить аргумент refaxes, вы сможете вычислять углы относительно локальных координат. В качестве иллюстрации на этом рисунке показан равномерный прямоугольный массив (URA) размером 5 на 5, повернутый относительно глобальных координат ( ) с помощью refaxes. Ось локальной системы координат ( ) выровнена с главной осью массива и перемещается по мере его движения. Длина пути не зависит от ориентации. Глобальная система координат определяет углы азимута и углы возвышения ( , ), а локальная система координат – углы азимута и углы возвышения ( , ).
Локальные и глобальные оси координат
Модель распространения в свободном пространстве
Details
Модель распространения сигнала в свободном пространстве гласит, что сигнал, распространяющийся из одной точки в другую в однородной, изотропной среде, движется по прямой линии, называемой линией видимости, или прямым лучом.
Прямая линия определяется геометрическим вектором от источника излучения до места назначения. Аналогичные предположения делаются и для гидролокатора, но вместо термина "свободное пространство" используется термин канал изоскорости.
Двулучевая модель распространения
Details
Двухлучевой канал распространения – это следующий шаг по сложности после канала свободного пространства и простейший случай многолучевой среды распространения. Канал свободного пространства моделирует прямолинейный путь по прямой видимости из точки 1 в точку 2. В двухлучевом канале среда задается как однородная, изотропная среда с отражающей плоской границей. Граница всегда устанавливается на = 0. Существует не более двух лучей, распространяющихся из точки 1 в точку 2. Первый луч распространяется по той же траектории прямой видимости, что и в канале свободного пространства. Траекторию прямой видимости часто называют прямой траекторией. Второй луч отражается от границы, прежде чем попасть в точку 2.
Согласно закону отражения, угол отражения равен углу падения. При симуляции ближнего радиуса действия, например, в системах сотовой связи или автомобильных радарах, можно предположить, что отражающая поверхность – земля или поверхность океана – плоская.
На рисунке показаны два пути распространения. Исходя из положения источника, , и положения приемника, , вы можете вычислить углы прибытия для обоих путей, и .
Углы падения – это углы возвышения и азимута приходящего излучения по отношению к локальной системе координат. В данном случае локальная система координат совпадает с глобальной системой координат.
Вы также можете вычислить углы передачи, и . В глобальных координатах угол отражения на границе совпадает с углами и .
Угол отражения важно знать, когда вы используете данные о потерях на отражение, зависящие от угла. Вы можете определить угол отражения, используя функцию rangeangle и установив оси отсчета в глобальную систему координат. Общая длина пути для траектории прямой видимости показана на рисунке , которая равна геометрическому расстоянию между источником и приемником. Общая длина пути для отраженной траектории равна . Величина – это расстояние между источником и приемником.
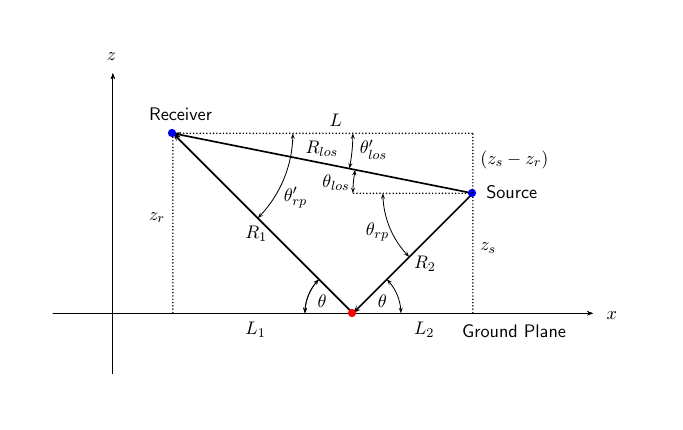
Вы можете легко вывести точные формулы для длины пути и углов в терминах дальности до земли и высоты объектов в глобальной системе координат.