Морфологические операторы
На этой странице описываются интерфейсы для основных морфологических операторов, которые можно использовать для построения собственного конвейера. Для наглядной иллюстрации результата действия различных операторов используется изображение с пятнами (blobs).
using TestImages, ImageBase
restrict(testimage("blobs"))|
Большинство операторов из этого пакета не поддерживают цветные изображения, если иное не указано явным образом. Связано это с тем, что многие морфологические операции основаны на сравнении значений пикселей: |
|
На этой странице представлена лишь часть экспортируемых функций. Недостающие функции будут добавлены в будущем. Чтобы найти нужную информацию, вам может потребоваться обратиться к странице с подробной справкой. Мы приветствуем участие пользователей в разработке документации. |
Операторы

Функция extreme_filter — это основная операция в ImageMorphology. Она напрямую используется во многих других морфологических операциях, таких как dilate и erode. На изображении показано дрожание пикселей, добавленное посредством функции случайного выбора.

Оператор расширения dilate, по сути, представляет собой фильтр максимума. Это базовое понятие в математической морфологии — многие операции строятся на основе операторов dilate и erode.
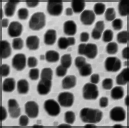
Оператор расширения erode, по сути, представляет собой фильтр минимума. Это базовое понятие в математической морфологии — многие операции строятся на основе операторов erode и dilate.

Оператор opening определяется как dilate(erode(img)). Очевидно, что операция открытия заполняет белые дыры на изображении.

Оператор closing определяется как dilate(erode(img)). Очевидно, что операция закрытия заполняет черные дыры на изображении.

Оператор «верх шляпы» (белый) определяется как img - opening(img). Очевидно, что этот фильтр может использоваться для выделения небольших белых элементов и деталей на изображении.

Оператор «верх шляпы» (черный), также известный как «дно шляпы», определяется как closing(img) - img. Очевидно, что этот фильтр может использоваться для выделения небольших черных элементов и деталей на изображении.

Существует три распространенных определения морфологического градиента: градиент Боше dilate(img) - erode(img), внешний половинный градиент dilate(img) - img и внутренний половинный градиент img - erode(img).

Оператор лапласиана определяется как разность внешнего и внутреннего градиентов: mgradient(img; mode=:external) - mgradient(img; mode=:internal).

Оператор морфологической реконструкции служит для многократного применения определенного оператора до достижения устойчивости, то есть неизменности результата. Чаще всего применяются реконструкция по расширению и реконструкция по эрозии.

underbuild представляет реконструкцию по расширению; это псевдоним для mreconstruct при op=dilate.

overbuild представляет реконструкцию по эрозии; это псевдоним для mreconstruct при op=erode.