Оптимальное потокораспределение

Это руководство было изначально предоставлено Джеймсом Фостером (James Foster, @jd-foster).

В этом руководстве формулируется и решается задача оптимального потокораспределения в сети переменного тока (AC-OPF) — хорошо изученная нелинейная задача из области электротехники.

После формулирования и решения нелинейной задачи мы сосредоточимся на получении хорошей оценки целевого значения в точке глобального оптимума с помощью полуопределенного программирования.

Одной из основных целей данного руководства является демонстрация имеющейся в JuMP возможности напрямую формулировать задачи с комплекснозначными переменными решения и комплексными матричными конусами, такими как объект HermitianPSDCone.

Другой пример моделирования с комплексными переменными решения см. в руководстве Quantum state discrimination, а дополнительные сведения см. в разделе Complex number support руководства.

В этом руководстве применяется матрично-ориентированный подход с упором на узлы сети, упрощающий построение полуопределенных программ. Другой подход заключается в формулировании задачи с упором на линии сети, что упрощает работу с ограничениями потока. Общий подход обеспечивается пакетом Julia и JuMP PowerModels.jl, который представляет собой фреймворк с открытым исходным кодом для широкого спектра формулировок моделей потокораспределения, включающий вспомогательные средства для работы с подробными сетевыми данными.

Требуемые пакеты

Для этого руководства требуются следующие пакеты:

using JuMP
import Clarabel
import DataFrames
import Ipopt
import LinearAlgebra
import SparseArrays
import Test

Первоначальная формулировка

В задачах оптимального потокораспределения при передаче электроэнергии обычно ставится следующий вопрос: каков наиболее экономически эффективный режим работы электрогенераторов при соблюдении ограничений, определяющих безопасные пределы для компонентов сети?

Для исследования этой задачи мы воспользуемся тестовым случаем сети с 9 узлами case9mod.

Представленный здесь граф сети содержит узлы (или шины) трех типов, каждый из которых имеет разное назначение: генерация (узлы 1, 2 и 3), передача (узлы 4, 6 и 8) и потребление (узлы 5, 7 и 9).

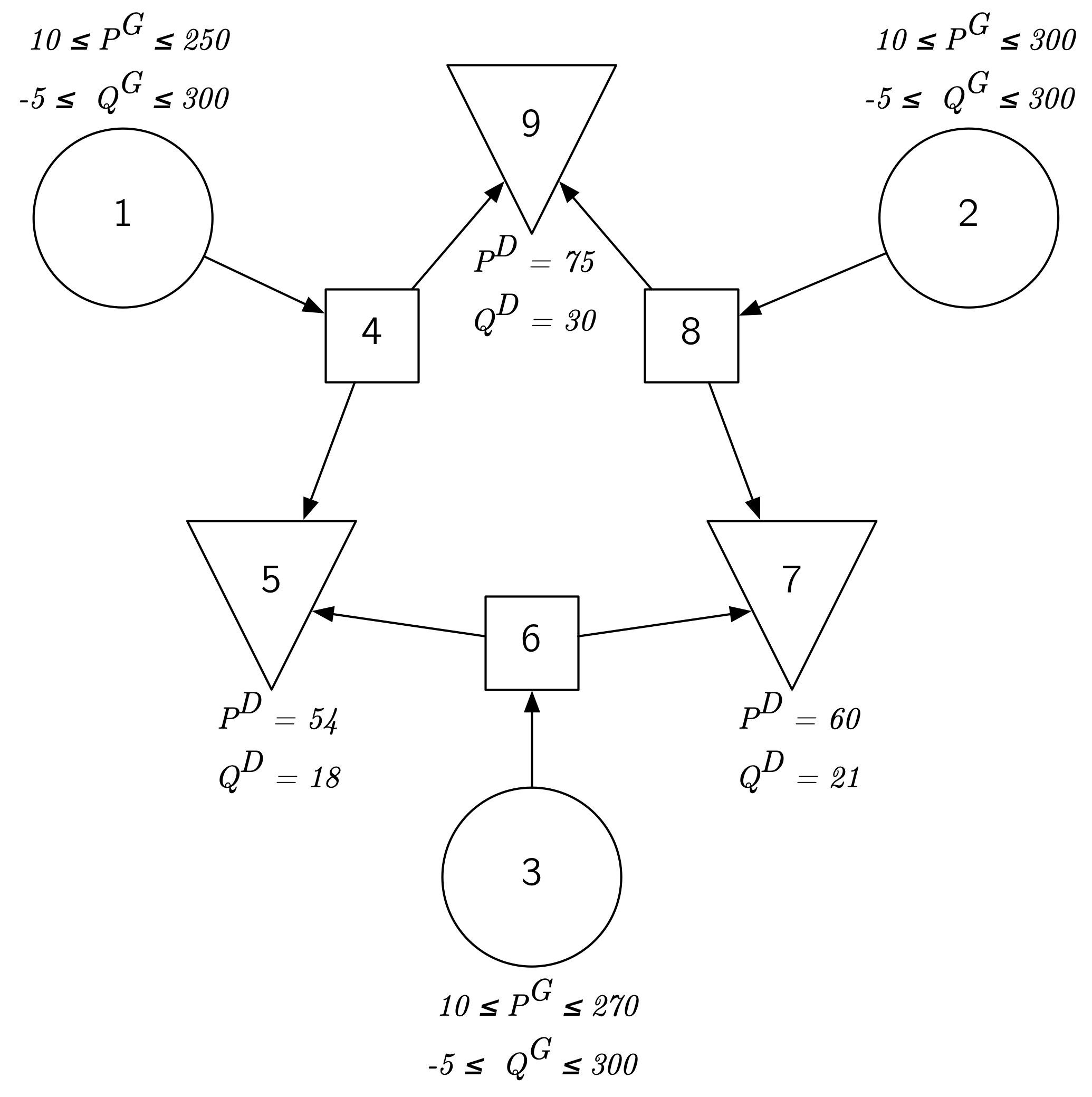
Этот пример представляет собой видоизмененную версию тестового случая case9 MATPOWER](https://matpower.org/) ([Zimmerman2011) (архив), разработанного Bukhsh2013 для своего архива тестовых случаев задач оптимального потокораспределения с локальными оптимумами. Этот тестовый случай также подробно рассмотрен в работе Krasko 2017.

Здесь термины шина и узел сети считаются синонимами, так же как и термины ветвь и линия передачи.

Для помощи в дальнейшем укажем количество узлов в сети:

N = 9;

Данные сети можно свести в несколько массивов. С помощью функции sparsevec из пакета стандартной библиотеки SparseArrays можно присвоить индексы и значения ненулевым точкам данных:

# Активная генерация: нижняя (`lb`) и верхняя (`ub`) границы
P_Gen_lb = SparseArrays.sparsevec([1, 2, 3], [10, 10, 10], N)
P_Gen_ub = SparseArrays.sparsevec([1, 2, 3], [250, 300, 270], N)
# Реактивная генерация: нижняя (`lb`) и верхняя (`ub`) границы
Q_Gen_lb = SparseArrays.sparsevec([1, 2, 3], [-5, -5, -5], N)
Q_Gen_ub = SparseArrays.sparsevec([1, 2, 3], [300, 300, 300], N)
# Уровни потребления электроэнергии (активный, реактивный, комплексная форма)
P_Demand = SparseArrays.sparsevec([5, 7, 9], [54, 60, 75], N)
Q_Demand = SparseArrays.sparsevec([5, 7, 9], [18, 21, 30], N)
S_Demand = P_Demand + im * Q_Demand

9-element SparseVector{Complex{Int64}, Int64} with 3 stored entries:
  [5]  =  54+18im
  [7]  =  60+21im
  [9]  =  75+30im

Ключевыми переменными решения являются введение активной мощности и введение реактивной мощности допустимым диапазоном генераторов. Для всех остальных шин переменные генерации должны быть ограничены значением 0. С другой стороны, эти негенерирующие узлы имеют фиксированную потребность в активной и реактивной мощности, обозначаемую и соответственно (для узлов передачи и генерации фиксированное значение 0).

Расходы на эксплуатацию каждого генератора моделируются как квадратичная функция его активной выходной мощности. В нашем тестовом случае минимизируемая целевая функция имеет следующий вид.

Давайте создадим первоначальную модель JuMP с некоторыми из этих данных:

model = Model(Ipopt.Optimizer)
set_silent(model)
@variable(model, P_Gen_lb[i] <= P_G[i in 1:N] <= P_Gen_ub[i])
@objective(
    model,
    Min,
    (0.11 * P_G[1]^2 + 5 * P_G[1] + 150) +
    (0.085 * P_G[2]^2 + 1.2 * P_G[2] + 600) +
    (0.1225 * P_G[3]^2 + P_G[3] + 335),
);

Еще до решения задачи оптимизации можно оценить нижнюю границу наилучшего целевого значения, подставив нижнюю границу в диапазон активной мощности каждого генератора (в данном случае всех десяти):

basic_lower_bound = value(lower_bound, objective_function(model));
println("Objective value (basic lower bound) : $basic_lower_bound")

Objective value (basic lower bound) : 1188.75

Оказывается, что целевые затраты в размере 1188,75 улучшить невозможно.

(Прямая подстановка возможна по той причине, что квадратичная функция одной переменной с положительными коэффициентами строго возрастает для всех .)

На самом деле мы можем сделать еще более быструю и даже более точную оценку из прямого наблюдения того, что вырабатываемая активная мощность должна быть равна потреблению активной мощности или превышать его:

@constraint(model, sum(P_G) >= sum(P_Demand))
optimize!(model)
@assert is_solved_and_feasible(model)
better_lower_bound = round(objective_value(model); digits = 2)
println("Objective value (better lower bound): $better_lower_bound")

Objective value (better lower bound): 2733.55

Однако должны соблюдаться и дополнительные ограничения потокораспределения.

Электроэнергия должна поступать из одного или нескольких узлов генерации по линиям передачи в узел потребления. Переменные состояния нашей стационарной электрической сети переменного тока представляют собой комплекснозначные переменные напряжения . Значения напряжения отражают как величину, так и фазу электрического состояния узла по отношению к остальной системе. В энергетической системе переменного тока также расширяется понятие сопротивления в проводах цепи постоянного тока до комплексной величины, известной как импеданс каждой линии передачи. Величина, обратная импедансу, называется адмиттансом. Вместе эти комплексные величины используются для выражения комплексной версии закона Ома: ток, протекающий через линию, пропорционален разнице напряжений на каждом конце линии, умноженной на адмиттанс.

Данные сети

Давайте соберем данные, необходимые для написания комплексных ограничений потокораспределения. Данные для задачи представляют собой список вещественных и мнимых частей импеданса линий. Из раздела branch data файла case9mod в формате MATPOWER получаем следующую таблицу данных:

branch_data = DataFrames.DataFrame([
    (1, 4, 0.0, 0.0576, 0.0),
    (4, 5, 0.017, 0.092, 0.158),
    (6, 5, 0.039, 0.17, 0.358),
    (3, 6, 0.0, 0.0586, 0.0),
    (6, 7, 0.0119, 0.1008, 0.209),
    (8, 7, 0.0085, 0.072, 0.149),
    (2, 8, 0.0, 0.0625, 0.0),
    (8, 9, 0.032, 0.161, 0.306),
    (4, 9, 0.01, 0.085, 0.176),
]);
DataFrames.rename!(branch_data, [:F_BUS, :T_BUS, :BR_R, :BR_X, :BR_Bc])

9×5 DataFrame

Row	F_BUS	T_BUS	BR_R	BR_X	BR_Bc
	Int64	Int64	Float64	Float64	Float64
1	1	4	0.0	0.0576	0.0
2	4	5	0.017	0.092	0.158
3	6	5	0.039	0.17	0.358
4	3	6	0.0	0.0586	0.0
5	6	7	0.0119	0.1008	0.209
6	8	7	0.0085	0.072	0.149
7	2	8	0.0	0.0625	0.0
8	8	9	0.032	0.161	0.306
9	4	9	0.01	0.085	0.176

Первые два столбца описывают сеть в виде исходящих и входящих точек соединения линий. В последних трех столбцах указаны сопротивление ветви, реактивное сопротивление ветви и реактивная проводимость линии.

Нам также понадобится ссылаться на число base_MVA (используемое для изменения масштаба):

base_MVA = 100;

и количество линий:

M = size(branch_data, 1)

На основе первых двух столбцов таблицы данных ветвей можно создать разреженную матрицу инцидентности, которая упрощает работу со структурой сети:

A =
    SparseArrays.sparse(branch_data.F_BUS, 1:M, 1, N, M) +
    SparseArrays.sparse(branch_data.T_BUS, 1:M, -1, N, M)

9×9 SparseMatrixCSC{Int64, Int64} with 18 stored entries:
  1   ⋅   ⋅   ⋅   ⋅   ⋅   ⋅   ⋅   ⋅
  ⋅   ⋅   ⋅   ⋅   ⋅   ⋅   1   ⋅   ⋅
  ⋅   ⋅   ⋅   1   ⋅   ⋅   ⋅   ⋅   ⋅
 -1   1   ⋅   ⋅   ⋅   ⋅   ⋅   ⋅   1
  ⋅  -1  -1   ⋅   ⋅   ⋅   ⋅   ⋅   ⋅
  ⋅   ⋅   1  -1   1   ⋅   ⋅   ⋅   ⋅
  ⋅   ⋅   ⋅   ⋅  -1  -1   ⋅   ⋅   ⋅
  ⋅   ⋅   ⋅   ⋅   ⋅   1  -1   1   ⋅
  ⋅   ⋅   ⋅   ⋅   ⋅   ⋅   ⋅  -1  -1

Вектор импеданса сети формируется из следующих двух столбцов:

z = (branch_data.BR_R .+ im * branch_data.BR_X) / base_MVA;

После чего вычисляется соответствующая матрица адмиттанса шины:

Y_0 = A * SparseArrays.spdiagm(1 ./ z) * A';

В то время как последний столбец содержит реактивную проводимость линии:

y_sh = 1 / 2 * (im * branch_data.BR_Bc) * base_MVA;

из которого получается матрица поперечного адмиттанса:

Y_sh = SparseArrays.spdiagm(
    LinearAlgebra.diag(A * SparseArrays.spdiagm(y_sh) * A'),
);

(Построение матрицы поперечного адмиттанса Y_sh выглядит несколько сложнее, чем построение Y_0, так как в расчеты должны добавляться только диагональные элементы; зарядный ток линии используется только в членах узлового напряжения, но не в членах линейного напряжения.)

Полная матрица адмиттанса шины $Y$ тогда определяется так:

Y = Y_0 + Y_sh;

Модель JuMP

Теперь мы готовы написать комплексные ограничения потокораспределения, необходимые для более точного моделирования электроэнергетической системы.

Мы введем ряд ограничений, моделирующих как физические, так и операционные требования.

Сначала инициализируем новую модель:

model = Model(Ipopt.Optimizer)
set_silent(model)

Затем создадим переменные узловой генерации электроэнергии:

@variable(
    model,
    S_G[i in 1:N] in ComplexPlane(),
    lower_bound = P_Gen_lb[i] + Q_Gen_lb[i] * im,
    upper_bound = P_Gen_ub[i] + Q_Gen_ub[i] * im,
)

9-element Vector{GenericAffExpr{ComplexF64, VariableRef}}:
 real(S_G[1]) + imag(S_G[1]) im
 real(S_G[2]) + imag(S_G[2]) im
 real(S_G[3]) + imag(S_G[3]) im
 real(S_G[4]) + imag(S_G[4]) im
 real(S_G[5]) + imag(S_G[5]) im
 real(S_G[6]) + imag(S_G[6]) im
 real(S_G[7]) + imag(S_G[7]) im
 real(S_G[8]) + imag(S_G[8]) im
 real(S_G[9]) + imag(S_G[9]) im

Нам нужны комплексные узловые напряжения (переменные состояния системы):

@variable(model, V[1:N] in ComplexPlane(), start = 1.0 + 0.0im)

9-element Vector{GenericAffExpr{ComplexF64, VariableRef}}:
 real(V[1]) + imag(V[1]) im
 real(V[2]) + imag(V[2]) im
 real(V[3]) + imag(V[3]) im
 real(V[4]) + imag(V[4]) im
 real(V[5]) + imag(V[5]) im
 real(V[6]) + imag(V[6]) im
 real(V[7]) + imag(V[7]) im
 real(V[8]) + imag(V[8]) im
 real(V[9]) + imag(V[9]) im

и операционные ограничения для поддержания уровней величины напряжения:

@constraint(model, [i in 1:N], 0.9^2 <= real(V[i])^2 + imag(V[i])^2 <= 1.1^2)

9-element Vector{ConstraintRef{Model, MathOptInterface.ConstraintIndex{MathOptInterface.ScalarQuadraticFunction{Float64}, MathOptInterface.Interval{Float64}}, ScalarShape}}:
 real(V[1])² + imag(V[1])² ∈ [0.81, 1.2100000000000002]
 real(V[2])² + imag(V[2])² ∈ [0.81, 1.2100000000000002]
 real(V[3])² + imag(V[3])² ∈ [0.81, 1.2100000000000002]
 real(V[4])² + imag(V[4])² ∈ [0.81, 1.2100000000000002]
 real(V[5])² + imag(V[5])² ∈ [0.81, 1.2100000000000002]
 real(V[6])² + imag(V[6])² ∈ [0.81, 1.2100000000000002]
 real(V[7])² + imag(V[7])² ∈ [0.81, 1.2100000000000002]
 real(V[8])² + imag(V[8])² ∈ [0.81, 1.2100000000000002]
 real(V[9])² + imag(V[9])² ∈ [0.81, 1.2100000000000002]

Кроме того, необходимо зафиксировать начало координат или опорный угол, относительно которого определяются все остальные комплексные углы напряжения (аргументы). Здесь мы используем узел 1 в качестве назначенной опорной шины. Фиксация мнимой части опорной шины в нулевом значении устанавливает ее комплексный угол напряжения на 0, в то время как ограничение вещественной части неотрицательными значениями запрещает эквивалентные решения, которые являются просто отражением на 180 градусов:

@constraint(model, imag(V[1]) == 0);
@constraint(model, real(V[1]) >= 0);

Уравнения потокораспределения выражают принцип сохранения энергии (мощности), где разница вырабатываемой и потребляемой мощности должна уравновешивать обмен мощности с сетью:

@constraint(model, S_G - S_Demand .== V .* conj(Y * V))

9-element Vector{ConstraintRef{Model, MathOptInterface.ConstraintIndex{MathOptInterface.ScalarQuadraticFunction{ComplexF64}, MathOptInterface.EqualTo{ComplexF64}}, ScalarShape}}:
 -1736.111111111111im real(V[1])² + 1736.111111111111im real(V[1])*real(V[4]) + 1736.111111111111 real(V[1])*imag(V[4]) - 1736.111111111111im imag(V[1])² - 1736.111111111111 imag(V[1])*real(V[4]) + 1736.111111111111im imag(V[1])*imag(V[4]) + real(S_G[1]) + imag(S_G[1]) im = 0
 -1600im real(V[2])² + 1600im real(V[2])*real(V[8]) + 1600 real(V[2])*imag(V[8]) - 1600im imag(V[2])² - 1600 imag(V[2])*real(V[8]) + 1600im imag(V[2])*imag(V[8]) + real(S_G[2]) + imag(S_G[2]) im = 0
 -1706.484641638225im real(V[3])² + 1706.484641638225im real(V[3])*real(V[6]) + 1706.484641638225 real(V[3])*imag(V[6]) - 1706.484641638225im imag(V[3])² - 1706.484641638225 imag(V[3])*real(V[6]) + 1706.484641638225im imag(V[3])*imag(V[6]) + real(S_G[3]) + imag(S_G[3]) im = 0
 1736.111111111111im real(V[4])*real(V[1]) - 1736.111111111111 imag(V[4])*real(V[1]) + 1736.111111111111 real(V[4])*imag(V[1]) + 1736.111111111111im imag(V[4])*imag(V[1]) + (-330.7378962025307 - 3930.8888726118976im) real(V[4])² + (194.21912487147264 + 1051.0682051867932im) real(V[4])*real(V[5]) + (1051.0682051867932 - 194.21912487147264im) real(V[4])*imag(V[5]) + (136.51877133105802 + 1160.409556313993im) real(V[4])*real(V[9]) + (1160.409556313993 - 136.51877133105802im) real(V[4])*imag(V[9]) + (-330.7378962025307 - 3930.8888726118976im) imag(V[4])² + (-1051.0682051867932 + 194.21912487147264im) imag(V[4])*real(V[5]) + (194.21912487147264 + 1051.0682051867932im) imag(V[4])*imag(V[5]) + (-1160.409556313993 + 136.51877133105802im) imag(V[4])*real(V[9]) + (136.51877133105802 + 1160.409556313993im) imag(V[4])*imag(V[9]) + real(S_G[4]) + imag(S_G[4]) im = 0
 (194.21912487147264 + 1051.0682051867932im) real(V[5])*real(V[4]) + (-1051.0682051867932 + 194.21912487147264im) imag(V[5])*real(V[4]) + (1051.0682051867932 - 194.21912487147264im) real(V[5])*imag(V[4]) + (194.21912487147264 + 1051.0682051867932im) imag(V[5])*imag(V[4]) + (-322.4200387138841 - 1584.0927014229458im) real(V[5])² + (128.20091384241147 + 558.8244962361526im) real(V[5])*real(V[6]) + (558.8244962361526 - 128.20091384241147im) real(V[5])*imag(V[6]) + (-322.4200387138841 - 1584.0927014229458im) imag(V[5])² + (-558.8244962361526 + 128.20091384241147im) imag(V[5])*real(V[6]) + (128.20091384241147 + 558.8244962361526im) imag(V[5])*imag(V[6]) + real(S_G[5]) + imag(S_G[5]) im = (54 + 18im)
 1706.484641638225im real(V[6])*real(V[3]) - 1706.484641638225 imag(V[6])*real(V[3]) + 1706.484641638225 real(V[6])*imag(V[3]) + 1706.484641638225im imag(V[6])*imag(V[3]) + (128.20091384241147 + 558.8244962361526im) real(V[6])*real(V[5]) + (-558.8244962361526 + 128.20091384241147im) imag(V[6])*real(V[5]) + (558.8244962361526 - 128.20091384241147im) real(V[6])*imag(V[5]) + (128.20091384241147 + 558.8244962361526im) imag(V[6])*imag(V[5]) + (-243.70966193142118 - 3215.386180510695im) real(V[6])² + (115.5087480890097 + 978.4270426363173im) real(V[6])*real(V[7]) + (978.4270426363173 - 115.5087480890097im) real(V[6])*imag(V[7]) + (-243.70966193142118 - 3215.386180510695im) imag(V[6])² + (-978.4270426363173 + 115.5087480890097im) imag(V[6])*real(V[7]) + (115.5087480890097 + 978.4270426363173im) imag(V[6])*imag(V[7]) + real(S_G[6]) + imag(S_G[6]) im = 0
 (115.5087480890097 + 978.4270426363173im) real(V[7])*real(V[6]) + (-978.4270426363173 + 115.5087480890097im) imag(V[7])*real(V[6]) + (978.4270426363173 - 115.5087480890097im) real(V[7])*imag(V[6]) + (115.5087480890097 + 978.4270426363173im) imag(V[7])*imag(V[6]) + (-277.22099541362326 - 2330.3249023271615im) real(V[7])² + (161.71224732461357 + 1369.7978596908442im) real(V[7])*real(V[8]) + (1369.7978596908442 - 161.71224732461357im) real(V[7])*imag(V[8]) + (-277.22099541362326 - 2330.3249023271615im) imag(V[7])² + (-1369.7978596908442 + 161.71224732461357im) imag(V[7])*real(V[8]) + (161.71224732461357 + 1369.7978596908442im) imag(V[7])*imag(V[8]) + real(S_G[7]) + imag(S_G[7]) im = (60 + 21im)
 1600im real(V[8])*real(V[2]) - 1600 imag(V[8])*real(V[2]) + 1600 real(V[8])*imag(V[2]) + 1600im imag(V[8])*imag(V[2]) + (161.71224732461357 + 1369.7978596908442im) real(V[8])*real(V[7]) + (-1369.7978596908442 + 161.71224732461357im) imag(V[8])*real(V[7]) + (1369.7978596908442 - 161.71224732461357im) real(V[8])*imag(V[7]) + (161.71224732461357 + 1369.7978596908442im) imag(V[8])*imag(V[7]) + (-280.4726852537284 - 3544.5613130217034im) real(V[8])² + (118.76043792911486 + 597.5134533308592im) real(V[8])*real(V[9]) + (597.5134533308592 - 118.76043792911486im) real(V[8])*imag(V[9]) + (-280.4726852537284 - 3544.5613130217034im) imag(V[8])² + (-597.5134533308592 + 118.76043792911486im) imag(V[8])*real(V[9]) + (118.76043792911486 + 597.5134533308592im) imag(V[8])*imag(V[9]) + real(S_G[8]) + imag(S_G[8]) im = 0
 (136.51877133105802 + 1160.409556313993im) real(V[9])*real(V[4]) + (-1160.409556313993 + 136.51877133105802im) imag(V[9])*real(V[4]) + (1160.409556313993 - 136.51877133105802im) real(V[9])*imag(V[4]) + (136.51877133105802 + 1160.409556313993im) imag(V[9])*imag(V[4]) + (118.76043792911486 + 597.5134533308592im) real(V[9])*real(V[8]) + (-597.5134533308592 + 118.76043792911486im) imag(V[9])*real(V[8]) + (597.5134533308592 - 118.76043792911486im) real(V[9])*imag(V[8]) + (118.76043792911486 + 597.5134533308592im) imag(V[9])*imag(V[8]) + (-255.27920926017288 - 1733.8230096448524im) real(V[9])² + (-255.27920926017288 - 1733.8230096448524im) imag(V[9])² + real(S_G[9]) + imag(S_G[9]) im = (75 + 30im)

Как и ранее, целевая функция представляет собой квадратичную стоимость активной мощности:

P_G = real(S_G)
@objective(
    model,
    Min,
    (0.11 * P_G[1]^2 + 5 * P_G[1] + 150) +
    (0.085 * P_G[2]^2 + 1.2 * P_G[2] + 600) +
    (0.1225 * P_G[3]^2 + P_G[3] + 335),
);

Наконец, мы готовы решить нелинейную задачу AC-OPF:

optimize!(model)
@assert is_solved_and_feasible(model)
solution_summary(model)

* Solver : Ipopt

* Status
  Result count       : 1
  Termination status : LOCALLY_SOLVED
  Message from the solver:
  "Solve_Succeeded"

* Candidate solution (result #1)
  Primal status      : FEASIBLE_POINT
  Dual status        : FEASIBLE_POINT
  Objective value    : 3.08784e+03

* Work counters
  Solve time (sec)   : 9.29689e-03
  Barrier iterations : 16

objval_solution = round(objective_value(model); digits = 2)
println("Objective value (feasible solution) : $(objval_solution)")

Objective value (feasible solution) : 3087.84

Генерируемая мощность (в прямоугольной форме) и комплексные значения напряжения (в полярной форме в градусах) в решении будут следующими:

DataFrames.DataFrame(;
    Bus = 1:N,
    ComplexPowerGen = round.(value.(S_G); digits = 2),
    VoltageMagnitude = round.(abs.(value.(V)); digits = 2),
    VoltageAngle_Deg = round.(rad2deg.(angle.(value.(V))); digits = 2),
)

9×4 DataFrame

Row	Bus	ComplexPowerGen	VoltageMagnitude	VoltageAngle_Deg
	Int64	Complex…	Float64	Float64
1	1	10.0-5.0im	0.91	-0.0
2	2	125.37-5.0im	0.92	12.37
3	3	57.03-5.0im	0.94	7.01
4	4	0.0+0.0im	0.91	-0.4
5	5	0.0+0.0im	0.92	-0.73
6	6	0.0+0.0im	0.94	4.84
7	7	0.0+0.0im	0.93	4.52
8	8	0.0+0.0im	0.93	7.12
9	9	0.0+0.0im	0.9	-0.63

Ослабления и более оптимальные границы целевой функции

Решатель Ipopt использует алгоритм внутренней точки. Он дает гарантии локальной оптимальности, но не может подтвердить, является ли решение глобально оптимальным. Найденное нами решение действительно является глобально оптимальным. Это было подтверждено в работах Bukhsh 2013 и Krasko 2017. Кроме того, это подтверждается различными решателями (такими как Gurobi, SCIP и GLOMIQO).

С помощью методов выпуклых ослаблений также можно улучшить текущую нижнюю границу:

better_lower_bound

2733.55

Для этого обратите внимание на то, что нелинейные ограничения в формулировке AC-OPF представляют собой квадратичные равенства потокораспределения и квадратичные неравенства напряжения.

Давайте преобразуем эти ограничения в линейную форму, сначала выполнив замену , где:

а — сопряженное транспонирование .

На первый взгляд, квадратичное ограничение границы напряжения, например:

для некоторых вещественных и в результате преобразуется в простую двухстороннюю границу:

А каждое квадратичное выражение для члена узловой мощности:

становится линейной комбинацией:

Здесь — это внутреннее произведение Фробениуса двух комплексных матриц, а обозначает матричную единицу с единственным ненулевым элементом 1 в строке и столбце .

E(k, n) = SparseArrays.sparse([k], [n], 1, N, N);

Естественно, мы перенесли нелинейность в ограничение равенства : именно это ограничение мы теперь ослабим, используя подход на основе полуопределенного программирования.

Мы используем комплексные напряжения и ослабим до

где отношение — это упорядочение в эрмитовом положительно полуопределенном конусе.

Приведенное выше ограничение эквивалентно следующему:

по теории дополнения Шура. Из этого матричного неравенства следует ряд конических ограничений второго порядка, принимающих определенные миноры матрицы для каждого :

что равносильно вещественному коническому неравенству второго порядка:

Мы также включили эти предполагаемые ограничения в демонстрационных целях.

Собрав все вместе, получаем следующее полуопределенное ослабление задачи AC-OPF:

model = Model(Clarabel.Optimizer)
set_attribute(model, "tol_gap_rel", 1e-3)
set_attribute(model, "tol_feas", 1e-3)
set_attribute(model, "tol_ktratio", 1e-3)
@variable(
    model,
    S_G[i in 1:N] in ComplexPlane(),
    lower_bound = P_Gen_lb[i] + Q_Gen_lb[i] * im,
    upper_bound = P_Gen_ub[i] + Q_Gen_ub[i] * im,
)
@variable(model, W[1:N, 1:N] in HermitianPSDCone())
@variable(model, V[1:N] in ComplexPlane(), start = 1.0 + 0.0im)
@constraint(model, [i in 1:N], 0.9^2 <= real(W[i, i]) <= 1.1^2)
@constraint(model, real(V[1]) >= 0)
@constraint(model, imag(V[1]) == 0)
@constraint(model, 0.9 <= real(V[1]) <= 1.1)
@constraint(model, LinearAlgebra.Hermitian([1 V'; V W]) in HermitianPSDCone())
# Неравенства миноров 2 x 2:
@constraint(
    model,
    [i in 1:N],
    [0.5, real(W[i, i]), real(V[i]), imag(V[i])] in RotatedSecondOrderCone()
)
@constraint(
    model,
    [i in 1:N],
    S_G[i] - S_Demand[i] == LinearAlgebra.tr((conj(Y) * E(i, i)) * W),
)
P_G = real(S_G)
@objective(
    model,
    Min,
    (0.11 * P_G[1]^2 + 5 * P_G[1] + 150) +
    (0.085 * P_G[2]^2 + 1.2 * P_G[2] + 600) +
    (0.1225 * P_G[3]^2 + P_G[3] + 335),
)
optimize!(model)

-------------------------------------------------------------
           Clarabel.jl v0.9.0  -  Clever Acronym
                   (c) Paul Goulart
                University of Oxford, 2022
-------------------------------------------------------------

problem:
  variables     = 117
  constraints   = 493
  nnz(P)        = 3
  nnz(A)        = 547
  cones (total) = 14
    : Zero        = 1,  numel = 19
    : Nonnegative = 2,  numel = (18,39)
    : SecondOrder = 9,  numel = (4,4,4,4,...,4)
    : PSDTriangle = 2,  numel = (171,210)

settings:
  linear algebra: direct / qdldl, precision: Float64
  max iter = 200, time limit = Inf,  max step = 0.990
  tol_feas = 1.0e-03, tol_gap_abs = 1.0e-08, tol_gap_rel = 1.0e-03,
  static reg : on, ϵ1 = 1.0e-08, ϵ2 = 4.9e-32
  dynamic reg: on, ϵ = 1.0e-13, δ = 2.0e-07
  iter refine: on, reltol = 1.0e-13, abstol = 1.0e-12,
               max iter = 10, stop ratio = 5.0
  equilibrate: on, min_scale = 1.0e-04, max_scale = 1.0e+04
               max iter = 10

iter    pcost        dcost       gap       pres      dres      k/t        μ       step
---------------------------------------------------------------------------------------------
  0   6.6673e+03  -3.0980e+05  4.75e+01  1.65e-02  7.87e-01  1.00e+00  3.34e+03   ------
  1   3.3968e+03  -6.4534e+04  2.00e+01  3.04e-03  2.44e-01  2.41e+02  9.42e+02  8.13e-01
  2   1.9798e+03  -1.7012e+04  9.59e+00  8.25e-04  9.73e-02  1.51e+02  3.06e+02  9.90e-01
  3   2.1414e+03  -2.3620e+03  2.10e+00  1.88e-04  2.03e-02  3.29e+01  7.63e+01  8.60e-01
  4   2.0597e+03   1.1123e+03  8.52e-01  3.78e-05  4.35e-03  5.52e+00  1.93e+01  8.55e-01
  5   1.6312e+03   1.4437e+03  1.30e-01  5.66e-06  6.85e-04  9.18e-01  3.20e+00  9.12e-01
  6   1.5768e+03   1.5579e+03  1.21e-02  5.34e-07  6.55e-05  9.28e-02  3.09e-01  9.19e-01
  7   1.5691e+03   1.5654e+03  2.35e-03  9.56e-08  1.22e-05  1.96e-02  5.73e-02  8.55e-01
  8   1.5657e+03   1.5640e+03  1.08e-03  3.99e-08  5.32e-06  8.54e-03  2.47e-02  7.64e-01
  9   1.5653e+03   1.5641e+03  7.26e-04  2.65e-08  3.55e-06  5.63e-03  1.64e-02  4.93e-01
---------------------------------------------------------------------------------------------
Terminated with status = solved
solve time =  426ms

Test.@test is_solved_and_feasible(model; allow_almost = true)
sdp_relaxation_lower_bound = round(objective_value(model); digits = 2)
println(
    "Objective value (W & V relax. lower bound): $sdp_relaxation_lower_bound",
)

Objective value (W & V relax. lower bound): 2754.02

Значения решения будут более наглядными, если округлить зашумленные данные:

W_1 = SparseArrays.sparse(round.(value.(W); digits = 2))

9×9 SparseMatrixCSC{ComplexF64, Int64} with 81 stored entries:
 1.19+0.0im   1.14-0.07im  1.13-0.05im  …  1.16-0.02im  1.14+0.05im
 1.14+0.07im   1.2+0.0im   1.15+0.02im     1.17+0.05im  1.15+0.12im
 1.13+0.05im  1.15-0.02im  1.19+0.0im      1.16+0.03im  1.14+0.1im
 1.15-0.03im  1.15-0.1im   1.15-0.08im     1.17-0.05im  1.15+0.03im
 1.15-0.05im  1.16-0.12im  1.15-0.1im      1.17-0.07im  1.16+0.01im
 1.16+0.01im  1.17-0.06im  1.16-0.03im  …  1.18-0.0im   1.16+0.07im
 1.15-0.01im  1.16-0.08im  1.16-0.06im     1.18-0.03im  1.16+0.05im
 1.16+0.02im  1.17-0.05im  1.16-0.03im     1.18+0.0im   1.16+0.07im
 1.14-0.05im  1.15-0.12im  1.14-0.1im      1.16-0.07im  1.15+0.0im

и восстановить аппроксимацию переменных напряжения:

DataFrames.DataFrame(;
    Bus = 1:N,
    Magnitude = round.(abs.(value.(V)); digits = 2),
    AngleDeg = round.(rad2deg.(angle.(value.(V))); digits = 2),
)

9×3 DataFrame

Row	Bus	Magnitude	AngleDeg
	Int64	Float64	Float64
1	1	0.95	-0.0
2	2	0.84	3.74
3	3	0.84	2.64
4	4	0.86	-1.24
5	5	0.86	-2.14
6	6	0.86	0.91
7	7	0.86	-0.2
8	8	0.86	1.12
9	9	0.85	-2.48

Дополнительные сведения об использовании разреженности см. в работе Jabr 2012.

Преимущество такого ослабления заключается в том, что можно работать непосредственно с комплексными напряжениями, чтобы расширить формулировку, усилить ослабление и получить дополнительную приблизительную информацию о переменных напряжения.