Wavelets
Пакет Julia для быстрых преобразований вейвлетов (одномерных, двухмерных, трехмерных, путем фильтрации или подъема). Пакет включает в себя дискретные преобразования вейвлетов, дискретные преобразования вейвлетов по столбцам и пакетные преобразования вейвлетов.
-
Вейвлеты 1-го поколения с использованием блоков фильтров (периодических и ортогональных). Имеются фильтры для вейвлетов следующих типов: Хаара, Добеши, койфлетов, симмлетов, Батла-Лемари, Бейлкина, Вайдьянатхана.
-
Вейвлеты 2-го поколения с использованием подъема (периодические и общего типа, включая ортогональные и биортогональные). В настоящее время включены схемы подъема только для вейвлетов Хаара и Добеши (разработка продолжается). Пользователи могут сами легко создавать новые схемы подъема. Текущая реализация преобразований подъема в два раза быстрее преобразований фильтрации.
-
Функции определения порога, наилучшего базиса и сглаживания, например сглаживания TI посредством циклического вращения, наилучшей основы для WPT, оценки шума, аппроксимации с преследованием. См. пример кода и изображение ниже.
-
Служебные средства для работы с вейвлетами, например индексирование и вычисление размера, масштабирование и вычисление вейвлет-функций, тестовые функции, повышение и снижение частоты выборки, зеркальные фильтры, подсчет коэффициентов, локальные циклические сдвиги и многое другое.
-
Служебные средства для построения графиков и визуализации одномерных и двухмерных сигналов.
Сведения о лицензии (MIT) см. в файле LICENSE.md.
В число других связанных пакетов входят WaveletsExt.jl и ContinuousWavelets.jl.
API
Преобразования вейвлетов
Функции dwt и wpt (а также обратные им) являются линейными операторами. Пример построения типа wt см. в описании wavelet ниже.
Дискретные преобразования вейвлетов
# DWT
dwt(x, wt, L=maxtransformlevels(x))
idwt(x, wt, L=maxtransformlevels(x))
dwt!(y, x, filter, L=maxtransformlevels(x))
idwt!(y, scheme, L=maxtransformlevels(x))Пакетные преобразования вейвлетов
# WPT (tree также может быть целым числом, что эквивалентно maketree(length(x), L, :full))
wpt(x, wt, tree::BitVector=maketree(x, :full))
iwpt(x, wt, tree::BitVector=maketree(x, :full))
wpt!(y, x, filter, tree::BitVector=maketree(x, :full))
iwpt!(y, scheme, tree::BitVector=maketree(y, :full))Типы вейвлетов
Функция wavelet — это конструктор типа для функций преобразования. Тип преобразования t может быть WT.Filter или WT.Lifting.
wavelet(c, t=WT.Filter, boundary=WT.Periodic)Классы вейвлетов
Модуль WT содержит типы для классов вейвлетов. В этом модуле определены константы такого вида, как WT.coif4, что служит сокращением для WT.Coiflet{4}(). Числа для ортогональных вейвлетов обозначают количество моментов исчезновения вейвлет-функции.
| Тип класса | База имен | Супертип | Числа |
|---|---|---|---|
|
haar |
|
|
|
coif |
|
2:2:8 |
|
db |
|
1:Inf |
|
sym |
|
4:10 |
|
batt |
|
2:2:6 |
|
beyl |
|
|
|
vaid |
|
|
|
cdf |
|
(9,7) |
Сведения о классе
WT.class(::WaveletClass) ::String # полное имя класса
WT.name(::WaveletClass) ::String # краткое имя типа
WT.vanishingmoments(::WaveletClass) # моменты исчезновения вейвлет-функцииСведения о типе преобразования
WT.name(wt) # краткое имя типа
WT.length(f::OrthoFilter) # длина фильтра
WT.qmf(f::OrthoFilter) # квадратурный зеркальный фильтр
WT.makeqmfpair(f::OrthoFilter, fw=true)
WT.makereverseqmfpair(f::OrthoFilter, fw=true)Примеры
Самый простой способ преобразования сигнала x выглядит так:
xt = dwt(x, wavelet(WT.db2))Тип преобразования может быть указан более явным образом (фильтр, периодический, ортогональный, 4 момента исчезновения):
wt = wavelet(WT.Coiflet{4}(), WT.Filter, WT.Periodic)Для периодической биортогональной схемы подъема CDF 9/7:
wt = wavelet(WT.cdf97, WT.Lifting)Преобразование вектора x:
# 5-уровневое преобразование
xt = dwt(x, wt, 5)
# обратное преобразование
xti = idwt(xt, wt, 5)
# полное преобразование
xt = dwt(x, wt)Другие примеры:
# фильтры легко масштабируются
wt = wavelet(WT.haar)
wt = WT.scale(wt, 1/sqrt(2))
# сигналы можно преобразовать на месте с помощью низкоуровневой команды,
# которая требует выделения очень небольшого объема памяти (особенно для фильтров с L=1)
dwt!(x, wt, L) # на месте (подъем)
dwt!(xt, x, wt, L) # запись в xt (фильтр)
# сглаживание с параметрами по умолчанию (задание строгих пороговых значений посредством VisuShrink)
x0 = testfunction(128, "HeaviSine")
x = x0 + 0.3*randn(128)
y = denoise(x)
# служебные средства для построения одномерных графиков (см. изображения и код в /example)
x = testfunction(128, "Bumps")
y = dwt(x, wavelet(WT.cdf97, WT.Lifting))
d,l = wplotdots(y, 0.1, 128)
A = wplotim(y)
# служебные средства для построения двухмерных графиков
img = imread("lena.png")
x = permutedims(img.data, [ndims(img.data):-1:1])
L = 2
xts = wplotim(x, L, wavelet(WT.db3))Графики Bumps и Lena:
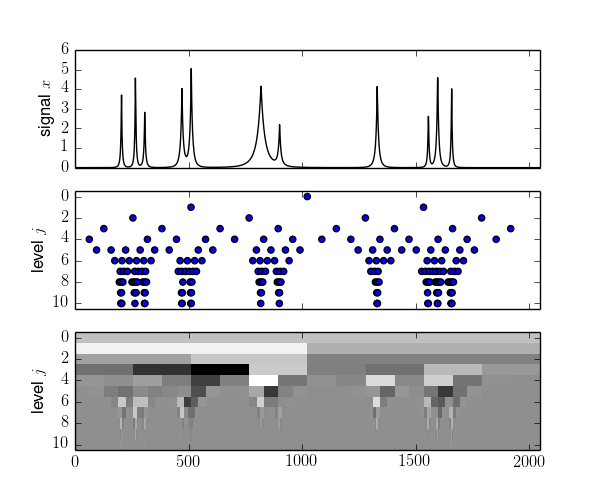
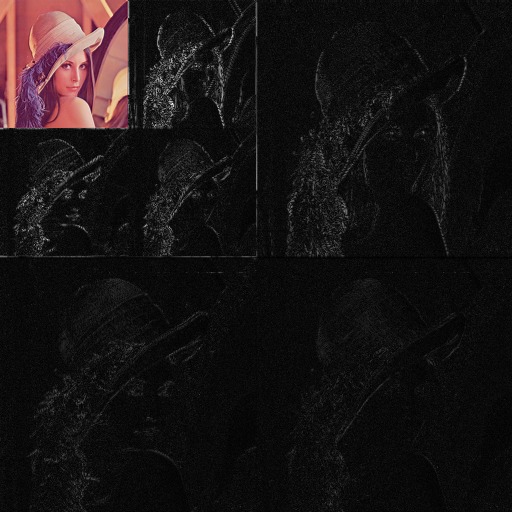
Определение порогов
Модуль Wavelets.Threshold включает в себя следующие служебные средства:
-
сглаживание (VisuShrink, инвариантное относительно переноса (TI));
-
наилучший базис для WPT;
-
оценка шума;
-
аппроксимация с преследованием;
-
функции определения порогов (типы см. в таблице).
API
# типы порогов с параметром
threshold!(x::AbstractArray, TH::THType, t::Real)
threshold(x::AbstractArray, TH::THType, t::Real)
# без параметра (PosTH, NegTH)
threshold!(x::AbstractArray, TH::THType)
threshold(x::AbstractArray, TH::THType)
# сглаживание
denoise(x::AbstractArray,
wt=DEFAULT_WAVELET;
L::Int=min(maxtransformlevels(x),6),
dnt=VisuShrink(size(x,1)),
estnoise::Function=noisest,
TI=false,
nspin=tuple([8 for i=1:ndims(x)]...) )
# энтропия
coefentropy(x, et::Entropy, nrm)
# наилучший базис для WPT, ограниченный активными начальными узлами дерева
bestbasistree(y::AbstractVector, wt::DiscreteWavelet,
L::Integer=nscales(y), et::Entropy=ShannonEntropy() )
bestbasistree(y::AbstractVector, wt::DiscreteWavelet,
tree::BitVector, et::Entropy=ShannonEntropy() )| Тип | Подробные сведения |
|---|---|
Определение порогов |
|
|
определение строгих порогов |
|
определение нестрогих порогов |
|
определение полустрогих порогов |
|
определение порогов Штейна |
|
определение положительных порогов |
|
определение отрицательных порогов |
|
аппроксимация наибольшего (наилучшего) m-члена |
Сглаживание |
|
|
Сглаживание VisuShrink |
Энтропия |
|
|
|
|
|
Примеры
Находит наилучшее базисное дерево для wpt и сравнивает его с dwt, используя аппроксимации наибольшего m-члена.
wt = wavelet(WT.db4)
x = sin.(4*range(0, stop=2*pi-eps(), length=1024))
tree = bestbasistree(x, wt)
xtb = wpt(x, wt, tree)
xt = dwt(x, wt)
# получаем аппроксимации наибольшего m-члена
m = 50
threshold!(xtb, BiggestTH(), m)
threshold!(xt, BiggestTH(), m)
# сравниваем разреженные аппроксимации по норме ell_2
norm(x - iwpt(xtb, wt, tree), 2) # наилучший базис wpt
norm(x - idwt(xt, wt), 2) # обычный dwtjulia> norm(x - iwpt(xtb, wt, tree), 2) 0.008941070750964843 julia> norm(x - idwt(xt, wt), 2) 0.05964431178940861
Сглаживание:
n = 2^11;
x0 = testfunction(n,"Doppler")
x = x0 + 0.05*randn(n)
y = denoise(x,TI=true)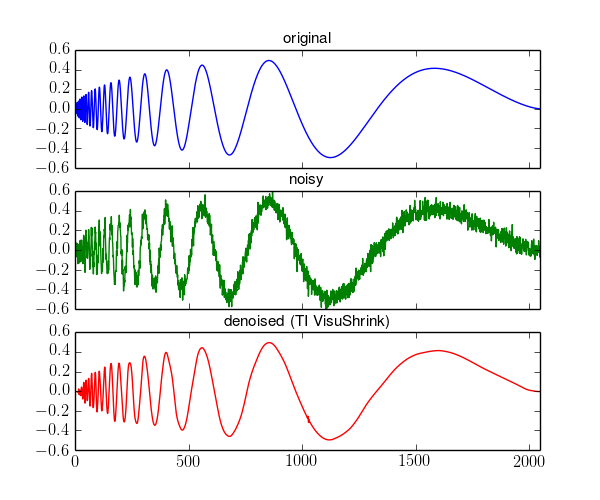
Тесты производительности
Время выполнения dwt (с использованием фильтра db2 длиной 4) и fft. Преобразования вейвлетов с подъемом выполняются быстрее и требуют меньше памяти, чем fft в одномерном и двухмерном случаях. dwt с подъемом в настоящее время выполняется в два раза быстрее, чем с фильтрацией.
# 10 итераций
dwt by filtering (N=1048576), 20 levels
elapsed time: 0.247907616 seconds (125861504 bytes allocated, 8.81% gc time)
dwt by lifting (N=1048576), 20 levels
elapsed time: 0.131240966 seconds (104898544 bytes allocated, 17.48% gc time)
fft (N=1048576), (FFTW)
elapsed time: 0.487693289 seconds (167805296 bytes allocated, 8.67% gc time)Для двухмерных преобразований (с использованием фильтра db4 и схемы подъема CDF 9/7):
# 10 итераций
dwt by filtering (N=1024x1024), 10 levels
elapsed time: 0.773281141 seconds (85813504 bytes allocated, 2.87% gc time)
dwt by lifting (N=1024x1024), 10 levels
elapsed time: 0.317705928 seconds (88765424 bytes allocated, 3.44% gc time)
fft (N=1024x1024), (FFTW)
elapsed time: 0.577537263 seconds (167805888 bytes allocated, 5.53% gc time)Используя низкоуровневую функцию dwt! и предварительное выделение памяти для временных массивов, можно добиться значительного выигрыша в плане использования памяти (и некоторого ускорения). Это полезно при многократном преобразовании.
Список будущих задач
-
Преобразования для неквадратных двухмерных сигналов
-
Расширения границ (кроме периодических)
-
Граничные ортогональные вейвлеты
-
Определение дополнительных схем подъема
-
WPT в двухмерном случае
-
Шкалограмма вейвлета
Связанные пакеты для работы с вейвлетами
-
Для непрерывного преобразования вейвлетов предназначен пакет ContinuousWavelets.jl.
-
WaveletsExt содержит следующие функции:
-
Стационарное преобразование
-
Пакетное разложение вейвлетов
-
Преобразование вейвлетов с автоматической корреляцией
-
Общий наилучший базис и наименее статистически зависимый базис
-
Локальный дискриминантный базис