ImageSegmentation.jl
Введение
Сегментация изображения — это процесс его разбиения на области со схожими атрибутами. Она имеет различные применения, например сегментация медицинских изображений и сжатие изображений, а также используется для предварительной обработки в задачах компьютерного зрения более высокого уровня, таких как обнаружение объектов и оптический поток. Данный пакет представляет собой набор алгоритмов сегментации изображений, написанных на Julia.
Пример
Сегментация изображения не является четко определенной математически задачей: так, единственное представление входного изображения без потерь предполагает, что каждый пиксель — это отдельный сегмент. Однако это не соответствует нашему интуитивному представлению о том, что некоторые пиксели группируются естественным образом. Поэтому многие алгоритмы требуют параметров. Зачастую это некоторый порог, отражающий допустимые вариации между пикселями в пределах одного сегмента.
Рассмотрим пример использования алгоритмов сегментации в этом пакете. Попробуем разделить лошадь, землю и небо на изображении ниже. Мы рассмотрим два алгоритма: выращивание областей от начальных точек и алгоритм Фельценшвальба. Для выращивания областей от начальных точек необходимо заранее знать количество сегментов и некоторые точки в каждом сегменте, тогда как алгоритм Фельценшвальба использует более абстрактный параметр, определяющий степень сходства внутри сегмента.

В документации по алгоритму seeded_region_growing указано, что ему требуются два аргумента: сегментируемое изображение и набор начальных точек для каждой области. Начальные точки должны храниться как вектор кортежей (position, label), где position — это CartesianIndex, а label — целое число. Начнем с того, что откроем изображение с помощью ImageView и считаем координаты начальных точек.
using Images, ImageView
img = load("src/pkgs/segmentation/assets/horse.jpg")
imshow(img)Наведите курсор на объекты, которые нужно сегментировать, и прочитайте координаты одной или нескольких точек внутри каждого из них. Мы сохраним начальные точки как вектор кортежей (seed position, label) и используем seeded_region_growing с записанными начальными точками.
using ImageSegmentation
seeds = [(CartesianIndex(126,81),1), (CartesianIndex(93,255),2), (CartesianIndex(213,97),3)]
segments = seeded_region_growing(img, seeds)
# output
Segmented Image with:
labels map: 240×360 Matrix{Int64}
number of labels: 3Все алгоритмы сегментации (кроме алгоритма нечетких C-средних) возвращают структуру SegmentedImage, в которой хранится результат сегментации. SegmentedImage содержит список примененных меток, массив назначенных каждому пикселю меток, а также средний цвет и количество пикселей в каждом сегменте. В этом разделе объясняется, как получить доступ к информации о сегментах.
julia> length(segment_labels(segments))
3
julia> segment_mean(segments)
Dict{Int64, RGB{Float64}} with 3 entries:
2 => RGB{Float64}(0.793598,0.839543,0.932374)
3 => RGB{Float64}(0.329863,0.35779,0.237457)
1 => RGB{Float64}(0.0646509,0.0587034,0.0743471)Мы можем визуализировать каждый сегмент, используя его средний цвет:
julia> imshow(map(i->segment_mean(segments,i), labels_map(segments)));
Такая форма отображения используется во многих примерах ниже.
Как видите, алгоритм неплохо справился с сегментацией трех объектов. Единственная очевидная ошибка заключается в том, что элементы неба, «обрамленные» лошадью, в итоге оказались сгруппированы с землей. Это связано с тем, что seeded_region_growing всегда возвращает связанные области, а пути, соединяющего эти части неба с остальной частью, нет. Если добавить несколько дополнительных начальных точек в этих областях и присвоить им ту же метку 2, что и остальной части неба, получится более или менее идеальный результат.
seeds = [(CartesianIndex(126,81), 1), (CartesianIndex(93,255), 2), (CartesianIndex(171,103), 2),
(CartesianIndex(172,142), 2), (CartesianIndex(182,72), 2), (CartesianIndex(213,97), 3)]
segments = seeded_region_growing(img, seeds)
Теперь сегментируем это изображение с помощью алгоритма Фельценшвальба. Алгоритму felzenszwalb нужен только один параметр k, который контролирует размер сегментов. Чем больше k, тем больше сегменты. При значениях от k=5 до k=500 обычно получаются хорошие результаты.
julia> using Images, ImageSegmentation
julia> img = load("src/pkgs/segmentation/assets/horse.jpg");
julia> segments = felzenszwalb(img, 100)
Segmented Image with:
labels map: 240×360 Matrix{Int64}
number of labels: 43
julia> segments = felzenszwalb(img, 10) #меньшие сегменты, но более зашумленная сегментация
Segmented Image with:
labels map: 240×360 Matrix{Int64}
number of labels: 312| k = 100 | k = 10 |
|---|---|
|
|
При k = 100 получаются лишь два «основных» сегмента. При k = 10 сегменты получаются меньше, но больше шума. felzenzwalb также принимает необязательный аргумент min_size — он удаляет все сегменты размером менее min_size пикселей. (Базовый алгоритм большинства методов не предполагает удаления небольших сегментов. С помощью метода prune_segments можно обработать результат сегментации и удалить мелкие сегменты.)
segments = felzenszwalb(img, 10, 100) # удаляет сегменты размером менее 100 пикселей
imshow(map(i->segment_mean(segments,i), labels_map(segments)))
Результат
Все алгоритмы сегментации (кроме алгоритма нечетких C-средних) возвращают на выходе структуру SegmentedImage. SegmentedImage содержит всю необходимую информацию о сегментах. Для получения информации о сегментах можно использовать следующие функции:
-
labels_map: It returns an array containing the labels assigned to each pixel -
segment_labels: It returns a list of all the assigned labels -
segment_mean: It returns the mean intensity of the supplied label. -
segment_pixel_count: It returns the count of the pixels that are assigned the supplied label.
Демонстрация
julia> img = fill(1, 4, 4);
julia> img[1:2,1:2] .= 2;
julia> img
4×4 Matrix{Int64}:
2 2 1 1
2 2 1 1
1 1 1 1
1 1 1 1
julia> seg = fast_scanning(img, 0.5);
julia> labels_map(seg) # возвращает карту присвоенных меток
4×4 Matrix{Int64}:
1 1 3 3
1 1 3 3
3 3 3 3
3 3 3 3
julia> segment_labels(seg) # возвращает список всех присвоенных меток
2-element Vector{Int64}:
1
3
julia> segment_mean(seg, 1) # возвращает среднюю интенсивность метки 1
2.0
julia> segment_pixel_count(seg, 1) # возвращает число пикселей с меткой 1
4Алгоритмы
Выращивание областей от начальных точек
Алгоритм выращивания областей от начальных точек сегментирует изображение относительно некоторых определенных пользователем начальных точек. Каждая начальная точка представляет собой кортеж (position, label), где position — это CartesianIndex, а label — положительное целое число. Каждая метка соответствует уникальной части изображения. Алгоритм пытается присвоить эти метки каждой из оставшихся точек. Если у нескольких точек одинаковая метка, они будут относиться к одному сегменту.
Демонстрация
julia> using Images, ImageSegmentation
julia> img = load("src/pkgs/segmentation/assets/worm.jpg");
julia> seeds = [(CartesianIndex(104, 48), 1), (CartesianIndex( 49, 40), 1),
(CartesianIndex( 72,131), 1), (CartesianIndex(109,217), 1),
(CartesianIndex( 28, 87), 2), (CartesianIndex( 64,201), 2),
(CartesianIndex(104, 72), 2), (CartesianIndex( 86,138), 2)];
julia> seg = seeded_region_growing(img, seeds)
Segmented Image with:
labels map: 183×275 Matrix{Int64}
number of labels: 2Исходное изображение (источник):

Сегментированное изображение, метки которого заменены средними значениями интенсивности:

Выращивание областей без начальных точек
Этот алгоритм похож на Seeded Region Growing, но не требует предварительной информации о начальных точках. Процесс сегментации начинается с области , содержащей один пиксель изображения. Допустим, что промежуточное состояние алгоритма состоит из множества идентифицированных областей . Пусть — это множество всех нераспределенных пикселей, которые граничат хотя бы с одной из этих областей. Процесс выращивания предполагает выбор точки и области , где ], таких, что
где |]
Если меньше threshold, то пиксель z добавляется в . В противном случае выбирается наиболее похожая область такая, что
Если меньше threshold, то пиксель z добавляется в . Если ни одно из этих двух условий не выполняется, то пиксель присваивается новой области . После присваивания обновляется статистика соответствующей области. Выполнение алгоритма останавливается, когда все пиксели присвоены какой-либо области.
Для unseeded_region_growing в качестве параметров требуются изображение img и порог threshold.
Демонстрация
julia> using ImageSegmentation, Images
julia> img = load("src/pkgs/segmentation/assets/tree.jpg");
julia> seg = unseeded_region_growing(img, 0.05) # здесь порог равен 0,05
Segmented Image with:
labels map: 320×480 Matrix{Int64}
number of labels: 698| Порог | Вывод | Процент сжатия |
|---|---|---|
Исходное изображение (источник) |
|
0 % |
0,05 |
|
60,63 % |
0,1 |
|
71,27 % |
0,2 |
|
79,96 % |
Алгоритм слияния областей Фельценшвальба
Этот алгоритм работает на основе графа смежности областей (RAG). Каждый пиксель или область представляет собой узел графа, а смежные пиксели или области соединены ребрами с весом, соответствующим расхождению между этими пикселями или областями. Алгоритм раз за разом объединяет сходные области, пока не получается окончательная сегментация. Он эффективно вычисляет «суперпиксели» с избыточной сегментацией на изображении. Функцию можно вызвать напрямую с изображением (реализация сначала создает граф RAG изображения, а затем продолжает работу).
Демонстрация
julia> using Images, ImageSegmentation, TestImages
julia> img = Gray.(testimage("house"));
julia> segments = felzenszwalb(img, 300, 100) # k=300 (порог слияния), min_size = 100 (минимальное количество пикселей на область)
Segmented Image with:
labels map: 512×512 Matrix{Int64}
number of labels: 11Теперь визуализируем сегментацию, создав изображение, на котором каждая метка заменена случайным цветом:
function get_random_color(seed)
Random.seed!(seed)
rand(RGB{N0f8})
end
imshow(map(i->get_random_color(i), labels_map(segments)))
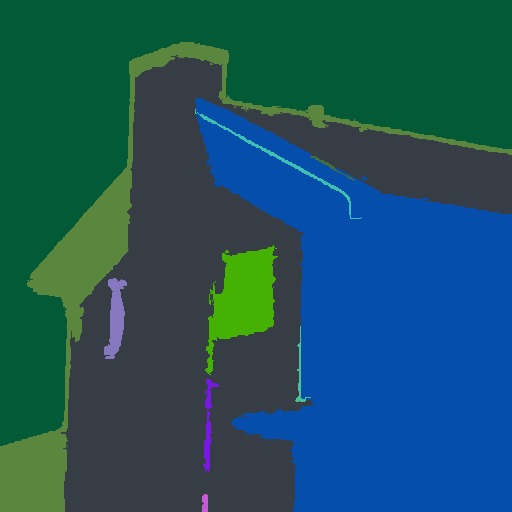
Сегментация методом среднего сдвига (MeanShift)
Метод среднего сдвига — это метод кластеризации. Его основные преимущества в том, что он не предполагает изначальной формы кластера (например, гауссиан для k-средних) и не нужно заранее знать количество кластеров. Этот алгоритм плохо масштабируется в зависимости от размера изображения.
Демонстрация
julia> using Images, ImageSegmentation, TestImages
julia> img = Gray.(testimage("house"));
julia> img = imresize(img, (128, 128));
julia> segments = meanshift(img, 16, 8/255) # параметры — это радиусы сглаживания: пространственный = 16, по интенсивности = 8/255
Segmented Image with:
labels map: 128×128 Matrix{Int64}
number of labels: 44

Быстрое сканирование
Алгоритм быстрого сканирования сегментирует изображение, сканируя его один раз и сравнивая каждый пиксель с соседними пикселями сверху и слева. Алгоритм начинает выполнение с первого пикселя и присваивает его новому сегменту . Количеству меток lc присваивается значение 1. Затем начинается обход изображения по столбцам, и для каждого пикселя вычисляется величина разницы diff_fn между ним и соседним с ним пикселем слева, допустим, , а также соседним с ним пикселем сверху, допустим, . Возможны четыре случая:
-
thresholdиthreshold: можно сказать, что точка имеет такую же интенсивность, как и соседняя с ней точка сверху. Следовательно, мы присваиваем точку сегменту, содержащему верхнюю соседнюю точку. -
thresholdиthreshold: аналогично случаю 1, мы присваиваем точку сегменту, содержащему левую соседнюю точку. -
thresholdиthreshold: точка существенно отличается от соседних с ней точек сверху и слева, поэтому ей присваивается новая метка , а значениеlcувеличивается. -
thresholdиthreshold: в данном случае верхний и левый сегменты объединяются, и рассматриваемая точка присваивается этому объединенному сегменту.
Этот алгоритм сегментирует изображение всего за два прохода (один для сегментации, другой для слияния), поэтому он выполняется очень быстро и может применяться в приложениях реального времени.
Временная сложность: , где — количество пикселей
Демонстрация
julia> using ImageSegmentation, TestImages
julia> img = testimage("camera");
julia> seg = fast_scanning(img, 0.1) # порог = 0.1
Segmented Image with:
labels map: 512×512 Matrix{Int64}
number of labels: 2538
julia> seg = prune_segments(seg, i->(segment_pixel_count(seg,i)<50), (i,j)->(-segment_pixel_count(seg,j)))
Segmented Image with:
labels map: 512×512 Matrix{Int64}
number of labels: 65Исходное изображение:

Сегментированное изображение:

Разделение областей с помощью деревьев областей
Этот алгоритм следует методологии «разделяй и властвуй». Если входное изображение однородное, то ничего не происходит. В противном случае изображение делится на две части по каждому измерению, и эти части сегментируются рекурсивно. В результате строится дерево областей, на основе которого можно создать сегментированное изображение.
Временная сложность: , где — количество пикселей
Демонстрация
julia> using TestImages, ImageSegmentation
julia> img = testimage("lena_gray");
julia> function homogeneous(img)
min, max = extrema(img)
max - min < 0.2
end
homogeneous (generic function with 1 method)
julia> seg = region_splitting(img, homogeneous)
Segmented Image with:
labels map: 256×256 Matrix{Int64}
number of labels: 8836Исходное изображение:

Сегментированное изображение, метки которого заменены средними значениями интенсивности:

Нечеткие C-средние
Нечеткая кластеризация C-средних широко применяется для неконтролируемой сегментации изображений. Это итеративный алгоритм, который пытается минимизировать функцию стоимости:
В отличие от метода K-средних, он допускает принадлежность пикселей двум или нескольким кластерам. Он широко используется в медицинской визуализации, например при нечеткой сегментации моделей ткани головного мозга. Обратите внимание, что обоим методам — нечетких C-средних и K-средних — присущ элемент случайности: при каждом выполнении можно получить существенно отличающиеся результаты.
Временная сложность: , где — количество пикселей, — количество кластеров, а — количество итераций.
Демонстрация
julia> using ImageSegmentation, Images
julia> img = load("src/pkgs/segmentation/assets/flower.jpg");
julia> r = fuzzy_cmeans(img, 3, 2)
FuzzyCMeansResult: 3 clusters for 135360 points in 3 dimensions (converged in 27 iterations)Если говорить кратко, r содержит два важных компонента:
-
centers— матрица3×Cцентральных положений для кластеровCв цветовом пространстве RGB. Ее можно извлечь как вектор цветов с помощьюcenters = colorview(RGB, r.centers). -
weights— матрицаn×Cтакая, чтоr.weights[10,2]будет весом 10-го пикселя в зеленом цветовом канале (цветовом канале 2). Визуализировать этот компонент можно так:centers[i]*reshape(r.weights[:,i], axes(img)).
Дополнительные сведения см. в документации по Clustering.jl.
Исходное изображение (источник)

Результат с интенсивностью пикселя = интенсивность в центре кластера * принадлежность пикселя к этому классу
| Пурпурные лепестки | Зеленоватые листья | Белый фон |
|---|---|---|
|
|
|
Морфологические водоразделы
Алгоритм морфологических водоразделов рассматривает изображение как топографическую поверхность, где яркие пиксели соответствуют пикам, а темные — впадинам. Алгоритм начинает затопление со впадин (локальных минимумов) этой топографической поверхности, а границы областей формируются при слиянии воды из разных источников. Если изображение зашумлено, такой подход приводит к чрезмерной сегментации. Для предотвращения чрезмерной сегментации применяются маркерные водоразделы: топографическая поверхность затапливается с заранее определенного набора маркеров.
Рассмотрим пример использования водоразделов для сегментации соприкасающихся объектов. Чтобы использовать водораздел, необходимо изменить изображение так, чтобы на новом изображении затопление топографической поверхности от маркеров отделяло каждую монету. Если измененное изображение зашумлено, затопление из локальных минимумов может привести к чрезмерной сегментации, поэтому также требуется способ нахождения положений маркеров. В этом примере требуемую топографическую структуру имеет обратное преобразование distance_transform изображения с определенными порогами (изображение dist) (сведения о том, как это работает, см. на этой странице). Мы можем определить пороги изображения dist, чтобы получить положения маркеров.
Демонстрация
julia> using Images, ImageSegmentation
julia> img = load(download("http://docs.opencv.org/3.1.0/water_coins.jpg"));
julia> bw = Gray.(img) .> 0.5;
julia> dist = 1 .- distance_transform(feature_transform(bw));
julia> markers = label_components(dist .< -15);
julia> segments = watershed(dist, markers)
Segmented Image with:
labels map: 312×252 Matrix{Int64}
number of labels: 24
julia> imshow(map(i->get_random_color(i), labels_map(segments)) .* (1 .-bw)) #отображает сегментированное изображение| Исходное изображение | Изображение с определенными порогами |
|---|---|
|
|
| Изображение с обратным дистанционным преобразованием | Маркеры |
|---|---|
|
|
| Сегментированное изображение |
|---|
|
Некоторые полезные функции
Создание графа смежности областей (RAG)
Граф смежности областей можно построить непосредственно на основе SegmentedImage с помощью функции region_adjacency_graph. Каждому сегменту соответствует вершина, а между соседними сегментами строятся ребра. Результатом является кортеж объектов SimpleWeightedGraph и словарь Dict(label=>vertex) с весами, присвоенными в соответствии с weight_fn.
julia> using ImageSegmentation, Distances, TestImages
julia> img = testimage("camera");
julia> seg = felzenszwalb(img, 10, 100);
julia> weight_fn(i,j) = euclidean(segment_pixel_count(seg,i), segment_pixel_count(seg,j));
julia> G, vert_map = region_adjacency_graph(seg, weight_fn);
julia> G
{70, 139} undirected simple Int64 graph with Float64 weightsЗдесь в качестве веса соединяющего ребра использовалась разница в количестве пикселей. Такая мера различия может быть полезна, если граф смежности областей необходимо использовать для удаления сегментов меньшего размера путем их слияния с наибольшим соседним сегментом. Еще одна полезная мера различия — евклидово расстояние между средними уровнями интенсивности двух сегментов.
Создание дерева областей
Дерево областей можно построить на основе изображения с помощью функции region_tree. Если изображение неоднородное, то оно делится пополам по каждому измерению, и функция вызывается рекурсивно для каждой части изображения. Результатом является объект RegionTree.
julia> using ImageSegmentation
julia> function homogeneous(img)
min, max = extrema(img)
max - min < 0.2
end
homogeneous (generic function with 1 method)
julia> t = region_tree(img, homogeneous) # `img` — это изображение
Cell: RegionTrees.HyperRectangle{2, Float64}([1.0, 1.0], [300.0, 300.0])Дополнительные сведения о RegionTrees см. здесь.
Отсечение ненужных сегментов
Все ненужные сегменты можно легко удалить из SegmentedImage с помощью функции prune_segments. Она удаляет сегмент, заменяя его соседним сегментом с наименьшим значением diff_fn. Можно передать список сегментов, подлежащих удалению. Можно также передать функцию, которая возвращает true для меток, которые необходимо удалить.
|
Метки итогового изображения |
В этом и следующем примерах (в разделе Removing a segment) используется образец изображения SegmentedImage. Его можно сгенерировать следующим образом:
julia> img = fill(1, (4, 4));
julia> img[3:4,:] .= 2;
julia> img[1:2,3:4] .= 3;
julia> seg = fast_scanning(img, 0.5);
julia> labels_map(seg)
4×4 Matrix{Int64}:
1 1 3 3
1 1 3 3
2 2 2 2
2 2 2 2
julia> seg.image_indexmap
4×4 Matrix{Int64}:
1 1 3 3
1 1 3 3
2 2 2 2
2 2 2 2
julia> diff_fn(rem_label, neigh_label) = segment_pixel_count(seg,rem_label) - segment_pixel_count(seg,neigh_label);
julia> new_seg = prune_segments(seg, [3], diff_fn);
julia> labels_map(new_seg)
4×4 Matrix{Int64}:
1 1 2 2
1 1 2 2
2 2 2 2
2 2 2 2Удаление сегмента
Удалить один сегмент можно с помощью функции rem_segment!. Она удаляет сегмент из SegmentedImage на месте, заменяя его соседним сегментом с наименьшим значением diff_fn.
|
Если необходимо удалить несколько сегментов, то следует отдать предпочтение функции |
julia> seg.image_indexmap
4×4 Matrix{Int64}:
1 1 3 3
1 1 3 3
2 2 2 2
2 2 2 2
julia> diff_fn(rem_label, neigh_label) = segment_pixel_count(seg,rem_label) - segment_pixel_count(seg,neigh_label);
julia> rem_segment!(seg, 3, diff_fn);
julia> labels_map(new_seg)
4×4 Matrix{Int64}:
1 1 2 2
1 1 2 2
2 2 2 2
2 2 2 2